7.0 Ausgangspunkt     ->7.1     ->Inhalts.Verz.
Bisher hatten wir dem "(abstrakten) Euklid. Raum", symb.: R^m , über die Richtungs-Axiomatik seiner Elemente, folgende Eigenschaften zugeordnet:
(1) Linearer-, metrischer- ,normierter Raum bzw. Raum mit Skalarprodukt.
Im Folgenden wird von Element-Mengen der Eigenschaften (1) ausgegangen, die nicht notwendigerweise Zahlen-Tupel sein müssen. Dies können z.B. stetige Funktionen in einem Intervall des Eukl.Raumes sein.
(Siehe dazu: Dok.3.9 "n-dim abstrakter Eukl. Raum" )

Die Problematik der linearen-, metrischen- und normierten Räumen wurde bereits vorher schon angesprochen, gehört aber in den jetzigen Kontext und ist deshalb Ausgangspunkt der Analysis.

Der Begriff der Abb. fußt auf der Axiomatik der Mengen-Verknüpfung. Dabei heißt die Zuordnungsvorschrift, die eine (Teil)Menge in eine andere (Teil)Menge transformiert: Abbildung.
Symb.: M2=Abb(M1), M1,M2 ⊂R
Besteht die Abb. aus einer zulässigen Verknüpfungs-Folge, und bildet sie die Elemente in die Menge der Zahlen ab, so heißt sie: "Funktion", ansonsten wird sie allg. "Operator" genannt.

Die bereits schon früher angesprochene Äquivalenz des Newton-Raumes mit dem Euklid.Raum (Menge aller m-Tupel Zahlen) erfordert einige grundlegende Überlegungen zu Interpretationen von Verknüpfungen im R^m zu Ereignissen im Newton-Raum:
Ereignisse, sind, ganz allg. alles, was man "erkennen" kann und somit Teil der sog. "Erkenntnis-Theorie". Diese besagt, daß ich nur "Erkenne", was ich "kenne". Z.B. wird der Betrachter eines Bildes im Bild den "Eifel-Turm" nur dann erkennen, wenn er weiß, daß es ihn gibt, wie er aussieht und evtl. ein Anderer ihm das erläutert hat.
Auf unsere Mathematik übertragen bedeutet das: In einem Produkt a*b erkennt der Eine eine Rechteck-Fläche mit Len=a und Breite=b, ein Anderer eine Batterie-Kapazität von a=6 Zellen mit je 2V.
Eine Division a/b könnte die Beschreibung eines Winkels sein usw.
Es wird also immer eine Verknüpfung von Elementen eines math.Raumes mit Ereignissen des Newton-Raumes assoziiert.

Besondere Bedeutung haben Verknüpf.-Folgen wie z.B. die Null-Summen-Differenz-Relation:
0=Sum(p_j - p_j) ,j=0,1,...n, die umgeformt werden kann zu:
0=(p₀ - p_n) +Sum(p_j -p_j-1) , j=1,2,..,n ,∀n≥1   =>
Δp =(p_n - p₀) =Sum(p_j -p_j-1) , j=1,2,..,n ,∀n≥1
= n-Teilung des Intervall's  (p₀,p_n) zu Folge {p_j}, j=0,1,..n

Term, Gleichung, Funktion, Abbildung sind die wichtigsten Grundbegriffe. Diese wiederum kennzeichnen bestimmte Beziehungen zwischen Punkten /Objekten verschiedener math. Räume.
Der einfachste math.Raum ist die Menge aller m-Tupel reeller Zahlen, also der sogenannte Eukl. Raum, symb.: R^m. Diese anschauliche Definition der "Analysis" wird am Beispiel des Term: Polynom erläutert.
Variable:   Mit 'Variable' bezeichnet man eine Menge von reell. Zahlen oder Elementen des R^m=1 , symb.: b={x}, x=beliebige reelle Zahl.
Folgerung:   Ein m-Tupel reeller Zahlen besteht aus m unabhängigen Variablen, die die Koord. der Elemente des R^m repräsentieren.
Term:   'Term' ist eine Folge zulässiger Verknüpfungen von Elementen des R^m, siehe Verknüpf.-Axiomatik im Euklid. Raum.
Polynom:   'Polynom' ist ein spezieller Term der Form:
P(x1,...xm)= Sum(v1,...,vm)[a_v1...vm (x^v1 ... x^vm) ] , a_(...) =reell.
Beispiel1:   P₂(x)= a₀ x⁰ +a₁ x¹ +a₂ x²
Beispiel2:   P₁(x,y)= a₀₀ x⁰y⁰ +a₀₁ x⁰y¹ +a₁₁ x¹y¹ , a₁₀=0
Bemerkung1:   P₁() heißt lineares Polynom
Bemerkung2:   Im Beispiel 2 ist P₁(x,y) ein Polynom=Term von 2 Variablen. Der Grad des Polynoms wird vom höchsten Koeff.≠0 bestimmt. Im Beispiel2 ist a₁₁≠0 höchster Koeff., alle a_i,j=0 , i>1, j>1

Wert eines Term:   Da zulässige Verknüpfungen von Elementen wieder ein Element ergeben, besitzt jeder Term einen reellen Wert. Sind die verknüpften Elemente ausschließlich Konstanten, dann ist der Wert ebenfalls eine Konstante.
Bei Verknüpfungen ein oder mehrerer Variablen stellt der Wert eine weitere Variable dar. Z.B. 2x= Wert(y), x,y reell.
Gleichung:   Setzt man einen Term mit seinem Wert gleich, so handelt es sich um eine 'Gleichung'. Siehe Beispiel zuvor.
Funktion:   Enthält die Gleichung Variablen, mind.2, dann wird die Gleichung auch 'Funktion' genannt. Der Begriff 'Funktion' wird hier allg. als Zuordnungsvorschrift von Variablen-Werten verstanden.
Ist der gleichzusetzende Wert eines Term's mit Variable(n) eine Variable, dann hat die Gleichung/Funktion eine explizite Form. Z.B. y=2x
Ist der gleichzusetzende Wert eines Term's mit Variable(n) eine Konstante, dann hat die Gleichung/Funktion eine implizite Form. Z.B. y-2x=0
Wichtiger Satz:   Eine(=1) Gleichung mit m-Variablen (einschl.Wert) reduziert die Anzahl unabhängiger Variablen auf (m-1). Ist m=1 dann wird der 'einen' Variablen als Wert eine Konstante zugeordnet. Der Wert ist also dann Lösung der Gleichung. Besteht die Gleichung, aus nicht zulässigen Verknüpfungen, dann ist die Lösung 'leer'. 'm' steht hier auch für Anzahl ='Dimension' von R¹ Räumen. Dimension=0 heißt, Wert ist constant.
Beispiel3:   1+x²=0 ,keine zulässigen Verknüpfungen, nicht lösbar!
Beispiel4:   2y+x²=3 ,implizite Form, zulässige Verknüpfung, lösbar, Dimension(Lösungsmenge) =2-1 =1

Abbildung:   In der Funktion repräsentiert jede Variable einen R¹, steht also interpretativ für eine (reelle) Koord. des R^m, für welche, ist zunächst egal.
Jede Variable ist stetige Menge (siehe Modell der reellen Zahlen) und die Lösungsmenge somit ebenfalls. Bei Dim(Lösungsmenge)=0 mutiert die stetige Menge aber zu einer einzelnen Zahl.
Baut man die m-Variablen einer Gleichung zu einem m-dim.Raum zusammen, so zerfallen die m-Variablen bei einer Gleichung in (m-1) unabhängige Variablen und 1 abhängige Variable. Die (m-1) unabhängigen Variablen bilden dann die Quell-Menge und die eine abhängige Variable die Ziel-Menge einer sogenannten Abbildung im R^m. Symb.: Abb.{ f(x1,x2,..,x_m)=0 } , f=implizite Form. Die "{}" zeigen an, daß es sich um eine Variablen-Menge handelt.

Graph einer Abbildung:   Manchmal ist es sinnvoll, Quell- und Ziel-Mengen einer Abbildung grafisch darzustellen. Dazu muß aber die Gleichung nach der Ziel-Variablen aufgelöst werden.
Symb.: G={ (x,y,z): F(x,y,z)=0 ,z=f(x,y) } ,die Ermittlung der expliziten Form f() ist dabei Gegenstand der "Auflösung's-Theorie".
Beispiel3:   G={ (x,y,z): x²+y²-z=0 } , Der Graph G ist eine Rotations-Parabel-Fläche um z-Achse, nach oben geöffnet, mit Scheitel-Punkt =(0,0,0). Die Dimension der Lösungs-Menge ist 3-1 =2, also 2-dimensional =Fläche.

Eigenschaften von Polynomen:  
a)   In dem, von den Variablen gebildeten, Raum überall (partiell) n-mal differenzierbar, n=Polynom-Grad.
b)   Polynom-Gleichungen 1. Grades der Form:
P₁(x₁...x_n): a₀ +a₁ x₁ +.... +a_n x_n =0   heißen 'lineare Gleichungen'.
Der Lösungs-Mechanismus 'linearer Gleichungen' ist Gegenstand der Linearen Algebra.

Im Folgenden werden Elemente auch als Punkte bezeichnet!
Def:   Eine Menge R heißt metrischer Raum, wenn für je 2 Elemente x,y ein Abstand d(x,y) definiert ist, wobei gilt :
- d(x,y)≥0 , d(x,y)=0, wenn x=y
- d(x,y)=d(y,x)
- d(x,y) ≤ d(x,z)+d(z,y) ,z∈R   Dreiecks-Ungleichung
Def:   Ist x°∈R , so heißt:
U_δ(x°) ={ x: d(x,x°)<δ } =Delta-Umg. von x°
Def:   Eine Menge M⊂R heißt offen, wenn mit jedem x°∈R auch eine ganze U_δ(x°) zu M gehört.
Def:   Ist M⊂R, so heißt x*∈R Häufungspunkt von M, wenn in jeder Delta-Umg. von x* wenigstens 1 (von x*) verschiedener Pkt. von M liegt.   (Ein Häufungspunkt liegt also inmitten eine Delta-Umgeb.)
Folgerung:   Gehören alle Häufungspunkte einer Menge M selbst zu M, so heißt M abgeschlossen (~kompakt).

Ordnet man jeder natürlichen Zahl n=1,2,... einen Punkt x_n von M zu, so erhält man eine Folge in R: {x_n}, n=1,2,..
Def:   Eine Folge {x_n} heißt konvergent, wenn es ein x*∈R gibt, so daß gilt:
δ>0 vorgegeben, => ∃N_δ: x_n∈U_δ(x*) , ∀n≥N_δ ,
d.h., alle x liegen ab einem best.Index n in einer beliebig vorgegebenen Delta- Umgebung des Grenzwertes.
Im Falle der Konvergenz schreibt man symb.:
Lim(x_n)=x* oder x_n->x* für n→∞ .

Wie bei Folgen im Eukl.Raum gilt auch in R:
Satz1:   Der Limes einer konvergenten Folge {x_n} ist eindeutig bestimmt.
Beweis:  Andernfalls hätte man 2 Grenzwerte x*,x° mit x*≠x° .
Daher ist d(x*,x°)>0. Es sei δ=d(x*,x°)/2:
Dann gibt es 2 Konvergenz-Kriterien:
(1)   x_n->x* => ∃N₁: d(x_n,x*)<δ , ∀n≥N₁ .
(2)   x_n->x° => ∃N₂: d(x_n,x°)<δ , ∀n≥N₂ .
Für n≥max(N₁,N₂) gilt dann nach Dreiecks-Unleichung:
d(x*,x°)≤ d(x*,x_n) +d(x_n,x°) <2δ = d(x*,x°)
Dies steht aber im Widerspruch zu: x*≠x°
Ende des Beweises

Satz2:   Es sei x_n->x* und y ein weiteres Element aus R. Dann gilt:   d(x_n,y)->d(x*,y)
Beweis:  d(x*,y) ≤ d(x*,x_n) + d(x_n,y) =>
(1)   d(x*,y) - d(x_n,y) ≤ d(x*,x_n)   Analog gilt:
d(x_n,y) ≤ d(x_n,x*) + d(x*,y) =>
(2)   d(x_n,y) - d(x*,y) ≤ d(x_n,x*)   Betrag von (1) und (2) bilden:
Also gilt zusammen: [d(x_n,y) - d(x*,y)] ≤ d(x_n,x*)
Wegen d(x_n,x*)->0 für n→∞ golgt hieraus die Behauptung.
Ende des Beweises

Fundamentalfolge:   {x_n}->x* sei konvergente Folge.
Dann kann man den Abstand von Folgen-Elementen abschätzen:
d(x_n,x_m) ≤ d(x_n,x*) + d(x*,x_m) < δ/2 +δ/2 =δ ,
wenn n hinreichend groß und m>n ist.   (Siehe Satz1 )
Def.:   Folgen, deren Elementabstände für hinreichend große Indizes n,m beliebig klein sind, werden als Fundamentalfolge bezeichnet. Konvergente Folgen sind automatisch F-Folge. Der Grenzwert von F-Folgen gehört nur bei abgeschlossenen Element-Mengen immer mit zur Menge.

Anderseits gibt es metrische Räume, in denen nicht jede F-Folge konvergent ist.
Beispiel1:   Der R^m ist ein vollständiger metrischer Raum, wenn man als Abstand für 2 Elemente x,y setzt:
d(x,y) = (+)Sqrt[(x₁-y₁)²+....+x_m-y_m)² ]   (Euklid. Abstand))

Beispiel2:   Die Menge R=R^m-{x°} ist zunächst ein metrischer Raum, wie im Beispiel1, aber 1Pkt fehlt. Dadurch ist R nicht vollständig, denn die Folge F={(x₁°+1/n,x₂°,...)}, n=1,2,... ist Fundamentalfolge, aber der Grenzwert für n→∞ ist x° und gehört nicht zu R, also ist F nicht konvergent in R.

Beispiel3:   Ein anderer Abstand im R^m wird definiert durch:
d'(x,y) = max(d(x_j-y_j)) , j=1,...,m
Es wird gezeigt, daß alle 3 Eigenschaften einer Metrik erfüllt sind:
1.   d'(x,y) ≥0 , d'(x,y)=0 ,für x=y (alle Koord. sind gleich)
2.   d'(x,y)=d'(y,x) wegen d(x_j-y_j)=d(y_j-x_j)
3.   Ist z ein 3.Punkt, so gilt in jeder Koord. j:
d(x_j-y_j) ≤ d(x_j-z_j) + d(z_j-y_j)
Also gilt auch: max(d(x_j-y_j)) ≤ max(d(x_j-z_j)) + max(d(z_j-y_j))
=> d'(x,y) ≤ d'(x,z) + d'(z,y)

Satz3:   Im R^m ist eine Folge genau dann konvergent, wenn die j-ten Koord. konvergent sind, auch bei Zugrundelegung der Metrik d'.
Beweis:  d(x_n-x*)->0 , wenn {x_n}->x* konvergiert.
Wegen Linearität des Eukl.Raumes gilt:
(1)   d(x_n-x*) ≤ d(x_n,1-x*₁)+...+d(x_n,m-x*_m)
Für jede Koord.Folge x_n,j gibt es ein Nj, so daß d(x_n,j-x*_j) <δ/m bei vorgegebenen δ ist.
Setzt man Nmax≥max(Nj), so gilt insbesondere für max(d(x_n,j-x*_j)) <δ/m und (1): d(x_n-x*) <δ*m/m; für n≥Nmax.
Ende des Beweises

Bemerkung:   Ein metrischer-Raum ist immer auch ein normierter-Raum, wenn man Norm(x) =d(x,0) setzt. (Siehe auch Pkt.7.7 unten!)

Die Kugel-Oberfläche wird durch F() bestimmt:
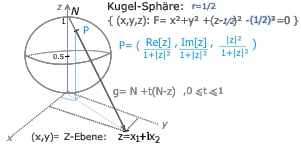
(1)   F= x² +y² +z²-z =0
N ist (0,0,1) und z=(x1,x2)= x1+i*x2 beliebiger Punkt in Z-Ebene.
Die durch N und z festgelegte Gerade g lautet: N+t(N-z) ,0≤t≤1
Also g:   (0,0,1) +t*(0-x1, 0-x2, 1-0) =>
g={(x,y,z): x=t*x1, y=t*x2, z=1-t , 0≤t≤1 } , N ->z
Es sollen die Schnittpunkte von g mit F bestimmt werden. Dazu wird g in Gl.(1) eingesetzt:
t²x1² +t²x2² +(1-t)² -1 +t =0   =>
t²x1² +t²x2² +t² -t =0   =>
t²(x1² +x2² +1) -t =0 , x1²+x2² =|z|² setzen, =>
t*[ t*(1+|z|²) -1] =0 , dies ergibt 2-t-Werte:
Es es existieren also 2 Schnittpunkte, die den Parametern t=0 und t= 1/(1+|z|²) entsprechen. t=0 liefert den Pkt.N , t= 1/(1+|z|²) einen zweiten Punkt P:
P= [x1/(1+|z|²) , x2/(1+|z|²) , 1-1/(1+|z|²) ]
( P= [Re[z]/(1+|z|²) , Im{z]/(1+|z|²) , 1-1/(1+|z|²) ])

Zu einem weiteren Pkt. z'=x1' +i*x2' der z-Ebene, ist P' der entspr. Punkt auf F:
P'= [x1'/(1+|z'|²) , x2'/(1+|z'|²) , 1-1/(1+|z'|²) ]
d(P,P'), Eukl.Metrik, ist dann: ( a=1+|z|² , a'=1+|z'|² setzen) :
d(P,P')²= (x1'/a'-x1/a)² + (x2'/a'-x2/a)² + (1/a'-1/a)²
    =   x₁'²/a'²   -2*x₁'²x₁²/a'²a²   + x₁²/a²
          + x₂'²/a'²   -2*x₂'²x₂²/a'²a²   + x₂²/a²
          + 1/a'²   -2*1/a'²a²   + 1/a²     , zusammenfassen :
    =   (x₁'² + x₂'² + 1)/a'²   + (x₁² + x₂² + 1)/a²  
          -2*(x₁'*x₁ + x₂'*x₂)/a'a     , (x₁² + x₂² + 1) =a setzten:
    =   1/a' +1/a   -2*(x₁'*x₁ + x₂'*x₂)/a'a
    =   (a' +a -2x₁'x₁ -2x₂'x₂) / a'a     , umformen zu :
    =   [ (x₁' + x₁)² + (x₂' + x₂)²] / a'a
Also ergibt sich d(P,P') zu:
d(P,P') = |z' - z| / Sqrt(1+|z'|)*Sqrt(1+|z|)

Folgerung:
Man erhält nun eine weitere Metrik d" in der Ebene, wenn man 2 Punkten z,z' als Abstand den gewöhnl. Eukl.Abstand der zugehörigen Punkte P,P' auf der Kugel Gl.(1) zuordnet. Man setzt also formal:
d"(z,z') = |z'-z| / Sqrt(1+|z'|)*Sqrt(1+|z|)



Beispiel:   Abstand auf Kugel-Oberfläche Erläuterung:
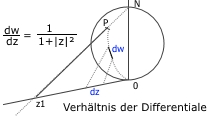
Die Punkte (N,0,z1,P) bilden ein rechtwinkliges Dreieck(Fläche), in dem auch der Großkreis durch N,0,P liegt.
Die Differentiale liegen ebenfalls im Dreieck und werden durch den Zoom-Faktor: 1/(1+|z|²) ineinander überführt.
Die Längen-Bestimmung auf der Kugel-Oberfläche, Len(0,P), kann deshalb auf die Länge von z1 zurückgeführt werden:
∫[0→P]*|dw| = ∫[0→z1]*|dz|/(1+|z|²)
Lösung:   Eine Stammfunktion zu 1/(1+|z|²) wäre: arctan()
Länge 0->N = arctan(∞) -arctan(0)= pi/2

Ausgangspunkt (abstrakter Raum):
Bis jetzt hatten wir für die reellen Zahlen, bzw. m-Tupel von reellen Zahlen, eine zulässige elementare Verknüpfung-Axiomatik für Add/Sub/skalare Mult. def., welche dann auf Funktionen, Approximation von Funktionen, Diff.-/Integral-Operator und Abb., erweitert wurde. Ausgangspunkt und Start sind hier immer die reellen Zahlen bzw. Punkte des Eukl.Raumes.
Nun wird dieser Ansatz verallgemeinert, indem man nicht die Zahlen in den Vordergrund stellt, sondern die Verknüpfungs-Axiomatik und diese auf beliebige Elemente einer Menge anwendet. Grob gesprochen ist ein abstrakter (linearer) Raum eine Element-Menge mit Verknüpfungs-Axiomatik.
In diesem Sinn ist der Eukl.Raum nur ein Spezialfall eines sogenannten "abstrakten Raumes".

Def:   Eine Menge R heißt linearer Raum, wenn zu je zwei Elementen x,y eindeutig eine auch zu R gehörige Summe (x+y) zugeordnet werden kann. Sei r=reell o. kompl. => r(x+y)∈R. In Verallg. kann jedes Element als Lin.Komb. L() von beliebigen Elementen dargestellt werden:
x=L(y₁...y_n) =Sum(c_j*y_j) , c_j sind Zahlen (reell/kompl.).
Bemerkung:   Der Index "n" muß nicht notwendig endl. sein!

Def. Skapro():   In R ist außerdem für je zwei Elemente x und y ein Skalarprodukt def., welches als Ergebnis eine Zahl ergibt. Das Skapro(x,y), Symb. <x,y> hat folg. Eigenschaften:
- <x,y> ist kompl. Zahl
- <x,x> ist stets eine nicht negative reelle/kompl. Zahl
- <x,x>=0 ⇔ x≡0
- <x,y>=<y,x>°   (c°=konj.kompl.Zahl.) Ist y=L() dann gilt:
Sind a,b kompl.Zahlen und x,y,z ∈R dann gilt insbesondere:
- <a·x +b·x ,z> =a·<x,z> +b·<y,z>,   Ist z=L() dann gilt:
- <x,Sum(c_j·y_j)> =Sum(c_j· <x,y_j> )
Folgerung1:
<z, a·x +b·x> =<a·x +b·x, z>° =(a·<x,z> +b·<y,z>)°
   = a°·<x,z>° +b°·<y,z>° = a°·<z,x> +b°·<z,y>

Def:   In einem Lin.Raum wird eine Norm zu x∈R wie folgt vereinbart:
Norm(x) =∥x∥ ≥0 , =0 nur, wenn x=0 ist.
∥x∥ =∥y∥ nur, wenn x=y ist.
Die Norm() hat die axiom.Eigenschaften wie im Eukl.Raum (insb.Dreiecks-Ungl.).
Im lin.Raum mit Skapro() wird die Norm wie folgt festgelegt:
Norm(x) =∥x∥ =sqrt(<x,x>)   oder: ∥x∥² =<x,x>

Basisprobleme im Lin.Raum R:
Def. Basis-Element:   Sei a∈R , p ein beliebiges weiteres Element, und es gilt stets:
p=c*a , c=Zahl. Dann heißt R "ein-dimensionaler Raum" ,Symb.: R¹, und a Basis-Element von R¹.
Achtung:   Der abstrakte Raum R¹ ist äquivalent zum Eukl.Raum R¹. Jedes Element vom R¹ ist Basis-Element und eine reelle Zahl! Das Element e = <a,a>/a² hat den Abstand 1 von Null und heißt "Eins-Element" des Raumes R¹. Das Element e ist eindeutig und kann aus jedem Element, siehe zuvor, gebildet werden.

Def. orthonormierte Basis:  
Eine Menge von m-Elementen e₁,...,e_m heißt orthonormiert, wenn für die paarweisen Skalarprodukte gilt <e_j,e_k> = d_jk :
  d_jk=0   für j≠k , Bedeutet im Eukl.Raum rechtwinklig
  d_jj=1   für j=k , Bedeutet im Eukl.Raum gleiche Richtung
Gibt es kein Element in R, welches nicht als Lin.Komb.L() von e₁...e_m gebildet/dargestellt werden kann, so heißt die Menge {e_j} "orthonormierte Basis" des Raumes R (im Eukl.Raum R^m mit Dimension m und Eins-Elemente e_j).

Stets sind m-orthonormierte Elemente linear unabhängig. Denn das Null-Element läßt sich durch Lin.Komb.L(), L=Sum(c_j*e_j), nur darstellen, wenn alle c_j=0 sind.
Bweis:
Es gilt Sum(c_j*e_j) =Null , beide Seiten mit e_k skalar mult. =>
Sum(c_j* <e_j,e_k> ) = Sum(c_j* d_jk) =c_k =0 ,∀k (=1...m). Daher sind alle c_j=0 und die orthonormierte Basis e₁,...,e_m linear unabhängig.
Ende des Beweises

Satz:   Werden alle Elemente als Richtung ab Null aufgefaßt, p=(p-0), so beginnen alle Basis-Elemente ab Null. (Im Eukl.Raum das sog. Karthesische Koord.-System)

Jedes Element x besitzt also eine eindeutig bestimmte Darstellung als Lin.Komb. der Basis-Elemente:
x=Sum(c_k*e_k) , k=1,...,m
Durch skalare Mult. mit e_j folgt:
<x,e_j> =<Sum(c_k*e_k),e_j> =Sum(c_k< e_k,e_j) =Sum(c_k* d_kj) =c_j
also ist c_j=<x,e_j>   => die allg. Form:
Gl.1:   x =Sum(<x,e_j>·e_j)
Dies ist die Form in Richtungs-cos(): <x,e_j>= ∣x∣ ·∣e_j∣ ·cos(x,e_j) = ∣x∣·1·cos(x,e_j)
also cos() in Richtung Basis-Achse
Folgerung2:
x=Sum(c_j*e_j) , y=Sum(d_k*e_k) sind 2 Elemente in Basis-Darstellung,
dann ist <x,y>= < Sum(c_j*e_j), Sum(d_k*e_k) >
    = Sum( c_j·d_k° < e_j, e_k> )   , wegen < e_j, e_k>= d_jk, folgt:
    = Sum( c_j·d_k° d_jk )   , wegen d_jk=1 für j=k ,sonst=0 folgt:
    = Sum( c_j·d_j° )   , also gilt:
Skapro(x,y) = Sum( c_j·d_j°)   ,Dies ist die allg. Konstrukt.-Formel für Skapro's , auch im Eukl.Raum!

Hinweis: In den folg. Kapiteln bedeutet ° =konj.komplex!

Sei f,g Elemente von R, f() und g() stetig auf I, dann wird ein Skapro() wie folgt def,:
Def.:    <f,g> = ∫(a→b)(f*g°)dx   , ° =konj.kompl.

Vorbemerkung zum Beweis:
Sind f und g in (a,b) diskrete Funktionen, z.B. durch eine Folge von Funktionswerten {f_j} /{g_j}, so ist das best.Integral eine endl. Summe über endl. viele f(x_j) /g(x_j):
<f,g> =Sum( f(x_j)·g(x_j)°)·Δx
Δx ist das Differential in (a,b), welches durch ein Normalisierungsprozess ensteht, der zu gleichen Abständen (=Δx zwischen je 2 Funktionswerten) im Intervall (a,b) führt.
Beispiel:   (f1g1° +f2g2° +f3g3°)Δx
Hier kann man f=(f1,f2,f3) und g=(g1,g2,g3) als zwei Richtungen im Raum auffassen, , zwischen denen ein Skapro() berechnet wird.
Zum Beweis werden noch einige Verküpf.Regeln für kompl.Werte benötigt:
- (z1 +z2)° =[(a+i*b) +(c+i*d)]° = [(a+c) +i*(b+d)]° =(a+c) - i*(b+d)
        =(a+i*b)° +(c+i*d)°
- (z1*z2)° =[(ac-bd) +i*(bc+ad)]° =(ac-bd) -i*(bc+ad) =(a-i*b)·(c-i*d)
        =(a+i*b)°·(c+i*d)°
- z1·z2° =(a+i*b)·(c-i*d) =(ac+bd) + i*(bc-ad)
- z1°·z2 =(a-i*b)·(c+i*d) =(ac+bd) - i*(bc-ad)
      => z1·z2° = (z1°·z2)°

Beweis der Axiomatik des Skapro's:
Das "∫" -Zeichen bedeutet im Folg. immer best.Integral über I :
a)   <f,f> =∫ (f*f°) dx =∫ ∣f∣² dx ≥0
Ist f(x)=0 ,∀x , dann ist ∫0 dx =0
Ist umgekehrt ∫ ∣f∣² dx ≥0 , so muß f(x)≡0 überall sein.
Denn: Ist z.B. f(x₀)≠0, so ist f(x) auch in einer ganzen δ-Umgebung:
(x₀-δ/2 ≤ x ≤x₀ +δ/2 ) ≠0 (Stetigkeit). Also kann δ so gewählt werden, daß f in U_δ(x₀) ≥f(x₀)/2 ist.
=> ∫ abs(f)² dx ≥ ∫ abs(f(x0))²/4 dx
   = abs(f(x0))²/4 *∫ dx =abs(f(x0))²/4 *δ  >0
Das heisst, in jeder δ-Umgeb. muß f≡0 sein.

b)   Eine kompl. Funktion h besteht aus Re[h] und Im[h] also:
h(x) =Re[h(x)] +i·Im[h(x)]
=>   (∫ h dx)° = ∫ Re[h]dx - i·∫ Im[h]dx , (∫ ausklammern: )
=>   (∫ h dx)° = ∫ (Re[h] - i·Im[h]) dx =∫ h° dx
Also ist:
<g,f>° =(∫ g*f° dx)° =∫ (g*f°)° dx =∫ g°f dx
    =∫ f·g° dx = <f,g>

c)   Sind  f,g,h  drei Funktionen aus R und a,b Zahlen, so ist:
<(a*f+b*g), h> = ∫ (a*f+b*g)·h° dx = a∫ f·h°dx +b∫ g·h°dx
    = a<f,h> +b<g,h>
  Folgerung 1:   <(a*f+b*g)°, h> =(a<f,h> +b<g,h>)°
    =a°<f,h>° +b°<g,h>° =a°<h,f> +b°<h,g>

Jetzt muß noch gezeigt werden, daß mit dem Skapro() eine Norm und damit eine Metrik(Abstand) gebildet werden kann.
Für 2 Elemente soll die folg.Ungleichung gelten:
Gl.1:   ∣<x,y>∣² ≤ <x,x><y,y>   , Schwarz'sche Ungleichung
Bemerkung:   Für diskrete Funktionen, endl. Anz. Funktionswerte, entspricht Gl.1 der Schwarz'schen Ungleichung für reelle Zahlen, wie im "Modell d. reellen Zahlen, Kap. 3.9" bereits bewiesen wurde.
Beweis der Gl.1:   für <x,y>≠0 , da sonst Gl.1 trivialer Weise erfüllt wäre, d.h., beide Elemente x,y sind ungleich Null. Neben x,y wird nun das Element z=(a*x +b*y) betrachtet:
a ist kompl. Zahl a= <x,y>°/∣<x,y>∣ , a°= <x,y>/∣<x,y>∣ und b=beliebige reelle Zahl.
Dann gilt für <z,z>: 0≤<z,z>   , Umformen entspr. c) =>
0≤<z,z> =< a*x+b*y, a*x+b*y>
   =a*<x,a*x+b*y> +b*<y,a*x+b*y>
   =a*<a*x+b*y,y>° +b*<a*x+b*y,y>° ,entspr.Folg.1:
   =aa°<x,x> +ab<x,y> +ba°<y,x> +b²<y,y>
Wegen aa° =a² =1 folgt:
   =<x,x> +b<x,y>°/∣<x,y>∣·<x,y>
          +b<x,y>/∣<x,y>∣·<x,y>° +b²<y,y>
   =<x,x> +2b∣<x,y>∣ +b²<y,y> , =quadrat. Gl. in b
Gl.2:  0≤ <x,x> +2b∣<x,y>∣ +b²<y,y>
Hier ist "b" eine belieb. reelle Zahl, also eine reelle Variable, und Gl.2 kann als quadr.Gl. dieser reellen Variablen (b) aufgefaßt werden. Insbesondere gilt Gl.2 auch für den Wert=0. daraus folgt die Nullstellen-Bestimmung für eine quadr.Gl. (x²+px+q), wobei alle Koeff.≠0 sind.
Gl.2a:   b² +2b·∣<x,y>∣/<y,y> +<x,x>/<y,y> =0
Lösung nach Formel:
=>   b_1,2 = -∣<x,y>∣/<y,y> ±sqrt( ∣<x,y>∣²/<y,y>² -∣<x,y>∣/<y,y> )
=>   b_1,2 =1/<y,y>·[ -∣<x,y>∣/<y,y> ±sqrt(∣<x,y>∣² -<x,x><y,y>) ]
Der Radikand kann nicht pos. sein, denn, dann würde es 2 verschiedene reelle Lösungen für die Nullstellen der quadr.Gl.2a geben. Das bedeutet, daß die reelle Variable "b" in der Umgeb. der Nullstellen, sowohl positive, als auch negative Werte annimmt, was im Widerspruch zu Gl.1 steht (≥0 also nicht negativ!)
Gl.1 muß aber überall positiv sein, weil alle Skapro's nach Voraussetzung größer Null sind.
Ergebnis: Radikand negativ oder Null, also keine reellen Nullstellen für Gl.2a,
=>   ∣<x,y>∣² ≤ <x,x><y,y>   , Schwarz'sche Ungleichung
Ende des Beweises Gl.1
Gl.1,"Schwarz'sche Ungleichung", besagt im vorliegenden Raum R:
∫ f·g dx ≤ ∫ ∣f∣²dx·∫ ∣g∣²dx

Bemerkung zum Beweis Gl.1:   Der Beweis der Schwarz'schen Ungleichung für eine unendl .Folge von Zahlen-Tupeln kann logischerweise nicht direkt, wie im Modell d. reellen Zahlen (endl. viele Tupel), erfolgen. Stattdessen wird das Skapro() eines willkürlich festgelegten Elementes z=(ax+by) mit sich selbst berechnet, also die Norm(z) =∥z∥ =<z,z>. Die Berechnung führt zu einer quadrat. Gl. der reellen Variablen "b" die, weil ∥z∥>0 sein muß, mit >0 ebenfalls abgeschätzt werden kann.
Eine quadr.Gl. mit pos.Koeff., die niemals negativ werden darf, kann aber keine reellen Nullstellen besitzen, sondern nur komplexe.
Beim vorliegenden indirektem Beweis wird nun geschlussfolgert, daß nur kompl.vorkommende Lösungen für "b" zu einem Widerspruch bei der Voraussetzung führen: "b" sei generell eine reelle Zahl".
Fazit: Die Festlegung des Elementes z=(ax+by) kann nur als "genialer Einfall" eines "genialen Mathematikers" bezeichnet werden, und ist ein klass.Beweis in der Math.Geschichte.

Satz:   Ein lin.Raum mit Skapro() ist immer auch ein normierter Raum, wenn man setzt:
∥x∥²=<x,x> oder ∥x∥=(+)sqrt(<x,x>)
Die Schwarz'sche Ungleichung: ∣<x,y>∣² ≤ <x,x><y,y>, schreibt sich dann:
∣<x,y>∣² ≤ ∥x∥²·∥y∥²   oder   ∣<x,y>∣ ≤ ∥x∥·∥y∥
Beweis:   Zum Beweis müssen die 3 axiomatische Eigenschaften der "Norm" nachgewiesen werden:
a)   wegen <x,x> ≥0  ist ∥x∥ ≥0
b)   ∥a·x∥ =sqrt(<a·x ,a·x>) =sqrt(aa°<x,x>) =∣a∣·∥x∥
c)  ∥<x+y>∥ =<x,y><x,y> = <x,x+y> +<y,x+y>
        =<x,x> +<x,y> +<y,x> +<y,y>
          ,wegen <x,y>+<x,y>° =reell =2∣<x,y>∣ gilt:
        =∥x∥² +∥y∥² +2∣<x,y>∣
          ,nach Ungeich.1., Kap.7.6 zuvor, ist ∣<x,y>∣ ≤ ∥x∥·∥y∥  =>
        ≤ ∥x∥² +∥y∥² +2∥x∥·∥y∥ =(∥x∥+∥y∥)²  =>
        ≤ ∥x∥+∥y∥
Ende des Beweises

Konvergenz im norm. lin.Raum:
Jeder norm. lin.Raum, also auch der lin.Raum mit Skapro(), ist gleichzeitig auch metrischer Raum, in dem Fundamental-Folgen und konvergente Folgen def. sind, durch:
d(x,y) =∥x-y∥ = sqrt(<x-y ,x-y>) .
Im Fall des Eukl.Raumes der reellen Zahlen wird die sog. "Eukl.Norm" verwendet:
d(x,y) =sqrt( (x₁-y₁)² +...+(x_m-y_m)²)
Satz: Es gilt also: x_n→x  <=>  <x_n,y>→<x,y>
Hierbei entspricht x_n→x der Konvergenz im lin.Raum mit Skapro(), die der Konvergenz <x_n,y>→<x,y> im Raum der reellen/kompl.Zahlen entspricht.
Beweis:   Nach den Umform-Regel für Skapro und anschließende Abschätzung mit der "Schwarz'schen Ungleichung" gilt:
∣<x_n,y> -<x,y>∣ = ∣<x_n-x,y>∣ ≤ ∥x_n-x∥·∥y∥ →0 , wegen ∥x_n→x∥ =0 , nach Voraussetzung.
Ende des Beweises

Folgen von Elementen aus R:
Def.:   n-Elemente e₁,..,e_n heißen orthonormiert, wenn Skapro(ej,ek)= d_jk ist. (Wie im Kap. 7.4 zuvor). Das bedeutet, alle e_j haben die Norm=1, je 2 versch. Eins-Basis-Elemente sind orthogonal.
Achtung: Wie Norm und Orthogonalität implementiert werden, spielt zunächst keine Rolle.
Def.:   Eine Folge von {e_j} ,j=1,2...,n heißt orthonormiert, wenn für jedes "n" die Elemente orthonormiert sind.

Beispiel:
Im Raum der stet. kompl.Funktionen im Interval I={x: 0≤x≤2pi} soll eine orthonormierte-Folge angegeben werden: (Skapro entspr. Kap.7.6 zuvor)
1.  (e^iax)°= (cos(ax) +isin(ax))°
        =cos(ax) -isin(ax)
        =cos(-ax) +isin(-ax) ,wegen gerade /ungerade Funk.
        =e^-iax
2.  Für kompl. a,b und best.Intergal ∫(0→2pi) gilt:
    Skapro(e^iax,e^ibx) =∫e^iax·e^-ibxdx
    =∫e^i(a-b)xdx = 1/i(a-b)[ e^i(a-b)2pi - e⁰] =0
wegen: e^i(a-b)2pi = cos(a-b)2pi +i sin(a-b)2pi = 1 + 0
    => 1- e⁰ =0.
3.  Skapro(e^iax,e^iax) =∫e^i(a-a)x =1
4.  Wir setzen: c=1/i(a-b) ,dann bilden die durch:
{ce^i0x ,ce^i1x , ce^i-1x,.., ce^i(±n)x } , n=1,2,..
def. kompl.Funktionen eine orthonormierte-Folge.

Def.:  Unter der linearen Hülle von k-Elementen p eines Raumes R versteht man die Menge aller x, die die Form haben:
x = a₁p₁ +...+ a_kp_k , a_j kompl. Zahlen

Satz:  Ist e₁,..,e_n eine orthonormierte Folge, so gilt:   e_n+1 ≠ L(e₁,..,e_n) ,∀n   ,d.h.: e_n+1 kann nicht als Lin.Komb. von e₁,..,e_n ausgedrückt werden, oder: e_n+1 ist orthogonal zu jedem e₁...e_n .
Beweis (indirekt:  Wäre e_n+1 ∈ L(e₁,..,e_n), so gäbe es Multiplikatoren b₁,..,b_n so daß gilt:
e_n+1 =Sum(b_j*e_j)   , durch skalare Mult. mit e_k folgt:
<e_n+1,e_k> =<Sum(b_j*e_j),e_k> =Sum(b_j< e_j,e_k>) =Sum(b_j* d_jk) =b_j   , siehe Kap.7.4 zuvor
also ist <e_n+1,e_k> =&=0 =b_j ,∀k ,k=1...n
=> alle b_j müssen Null sein, woraus folgt, daß die Annahme falsch ist, und die Behauptung im Satz: "e_n+1 ist orthogonal zu jedem e₁...e_n" stimmt.
Ende des Beweises

Im folg. Kapitel wird untersucht, wie aus einer beliebigen Element-Folge eine orthonormierte Folge gezimmert werden kann.

Ausgangspunkt ist eine Element-Folge a₁,a₂... , die folg. Bedingung erfüllt:
Alle a_j≠0 und a_n+1∉L(a₁,..,a_n) ,∀n
Bemerkung:  ∀n bedeutet, von n=2 aus, schrittweise, ist das n-te Element a_n lin.unabhängig von (a₁,..,a_n-1) , kann also nicht als Lin.Komb. der vorherigen Elemente berechnet werden. Beispiel: a1=(2,3) , a2=(4,6)   => a2 ist nicht lin.unabhängig, weil a2=2*a1 ist.

Grundlage des Verfahrens ist die Darstellung eines Elementes in Form der Richt.cos() in Richtung orthonormierten Basis-Elementen e₁...e_n, siehe Gl.1 aus Kap.7.4 zuvor, ganz unten:   x=Sum(<x,e_j>·e_j)
Erläuterung:  a₁,a₂ seien Elemente:
e₁ = a₁/Norm(a₁)   e₁ ist 1. Basis
  c =(a₂ -<a₂,e₁>e₁) setzen, dann 2.Schritt:
e₂ = c/Norm(c)  e₂ ist dann 2. Basis:
, denn <e1,e1>=<e2,e2>=1 und: <e2,e1>= c*a1 =(a₂ -<a₂,e₁>e₁)*a1
   =(a₂*e1 - <a₂,e₁>e₁*e1)   , wegen= e1=a1/.. folgt:
   =(<a₂,e1> - <a₂,e₁>*1)/.. =0

Verfahren:  Hat man von {a₁,a₂,a₃,...} a1,a2 → e1,e2 orthonormiert, wie in "Erläuterung:" zuvor beschrieben, dann wird:
a3' =(a₃ -<a₃,e₁>e₁ -<a₃,e₂>e₂) und e₃ =a3' /∥a3' ∥ gesetzt.
allg: a_n'= (a_n -Sum(<a_n,e_j>e_j)) , e_n =a_n' /∥a_n'∥  , j=1...n-1
Alle a₁...a_n seien bereits so orthonormiert zu e1,e2,...
Beweis (vollst.Induktion):  Wir überprüfen die Orthogonalität des Elementes e_n+1 durch skalare Mult. mit allen e_k ,k=1...n :
<e_n+1,e_k> =c*(<a_n+1,e_k> - Sum(<a_n+1,e_j><e_j,e_k>))   , j=1...n
        =c*(<a_n+1,e_k> - Sum(<a_n+1,e_j>d_jk))  , d_jk=1 für j=k
   =>  c*(<a_n+1,e_k> -<a_n+1,e_k>*1) =0   ,∀k
Ende des Beweises

Folgerung:  Ist {e₁,..,e_n} eine orthonormierte Folge aus den Elementen {a₁,..,a_n} ,so gilt: L(e₁,..,e_n) = L(a₁,..,a_n)

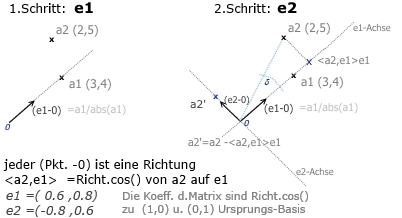
Bespiel_1:  a1=(3,4) , a2=(2,5)
e1= a1/5 =(3/5 ,4/5) =(0.6 ,0.8)   ,<a₂,e₁> =2*0.6 +5*0.8 =26/5
   a2' = a2 -<a₂,e₁>e₁ =(2,5 -26/5*( 0.6 ,0.8) =(-1.12 ,0.84)
    ∥ a₂'∥ = Sqrt(1.96) = 1.4
e2= a2`/Norm(a2') =(-0.8 ,0.6)   ,<e₂,e₁> =-0.2 +0.2 =0
    ∥ e₁'∥ = 0.36 0.64 =1  , ∥ e₂'∥ = 0.64 +0.36 =1
Matrix(e1,e2):
⌈ 0.69  0.8 ⌉
⌊-0.86  0.6 ⌋   => Det(e1,e2) = +1
Jetzt vertauschen wir a1⇔a2:

Bespiel_2:  a1=(2,5) , a2=(3,4)
e1= 1/Sqrt(29)*(2,5) =(0.37139 ,0.92848)
   <a₂,e₁> =1/Sqrt(29)*(3*2+4*5) =26/Sqrt(29)
   a2' = (3-26*2/Sqrt(29) ,4-46*5/Sqrt(29)) = (1.2069 ,-0.4828)
    ∥ a₂'∥ = Sqrt(1.4566 +0.23305) =1.2999
e2= (0.92846 , -0.37141)  
  <e₂,e₁> = (0.37139*92846 -0.92848*0.37141) = 0.34486-0.34485  ≈ 0
    ∥ e₁'∥ = Sqrt( ...)  ≈ 1
    ∥ e₂'∥ = Sqrt(0.86294 +0l.13795)  ≈ 1
Det(e1,e2):
⌈ 0.37139 0.92848 ⌉
⌊ 0.92846 -0.37141 ⌋   , ad-bc:
-0,1379379599 -0,8620565408 = -0,9999945007 ≈ -1

Folgerung:  Die Basis in Beispiel_2 hat eine andere Orientierung als die in Biespiel_1,
d.h., die Reihenfolge in {a_j} ist für die endgültige Orientierung bezüglich der Ursprungs-Basis {(1,0),(0,1} entscheident. Vertauschung von 2-benachbarten Basis-Elementen bedeutet: Mult. mit -1.

Folgerung:  Die Matrix (e1,e2) im Beispiel_1 zuvor entspricht der allg.Form:
⌈  a  b ⌉
⌊ -b  a ⌋   ,Siehe Beispiel in Kap.7.5 zuvor

Fazit:  Das Schmidt'sche Orthogonalisierungs -Verfahren bringt mit einer Folge {a_j} von n-Elementen eine orthonormierte Basis-Eins-Folge {e₁,}e₂,..} hervor, die mit der Basis-Folge der Eins-Elemente im Eukl.Raum die gleiche Orientierung hat. Dies ist wichtig für z.B. Koord. Transformationen.

Geometr. Interpretation des Verfahrens:

 Bild , Analysis2_3.jpg

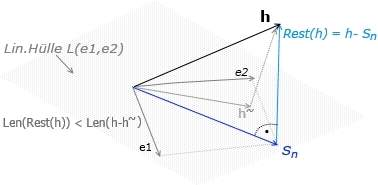
h˜ sei beliebiges Element aus der lin.Hülle L(e₁,...,e_n), also h˜=Sum(c_je_j) , cj kompl.
h sei allg. Element in R   und S_n=Sum(<h, e_j>e_j) ein, zu h gehöriges, spez. Element aus L().
Also gilt: Rest(h)= h-S_n   , ist  L()=R , dann ist Rest(h)=0 !
Problem: Welches Element aus L() liegt dem allg.Element h am nächsten?

Satz1:   Norm(h-S_n) ≤ Norm(h-h˜)  , das bedeutet:
a)   Kein Element h˜ aus L() hat von h einen kleineren Abstand als S_n   ,außerdem gilt:
b)   Sum∣<h,e_j>∣² ≤ Norm(h)²   , S_n ist kürzer als h
c)   <h-S_n ,h˜> =0  ⇔ Rest(h) ist orthogonal zu jedem h˜
Geometr. Interpretation des Satzes:
Beweis:   Der Beweis wird für h ∉ L() geführt, für h ∈ L() ist Satz trivial.
zu c)   <h-S_n ,h˜> = <h,h˜> - <S_n,h˜>
    <h,h˜> = Sum(<h, c_je_j>) = Sum( c_j°<h,e_j>)
    <S_n,h˜>=Sum(<h, e_j><e_j, c_je_j>) =Sum(c_j°<h, e_j>)
  =>   <h-S_n ,h˜> =0
zu b)   0≤ <h-S_n, h-S_n>= <h, h-S_n> - <S_n, h-S_n>
    = <h,h> -(<h, S_n> +<h, S_n>°) +< S_n,S_n>
        <h, S_n> +<h, S_n>° = 2·Re[<h, S_n>] = 2·Re[<h, Sum(<h, e_j>e_j)]
              => 2·Re[Sum(<h, e_j><h, e_j>)] = 2·Sum∣<h, e_j>∣²
           < S_n,S_n> =< Sum(<h, e_j>e_j) , Sum(<h, e_j>e_j) >
              => Sum( <h, e_j> <h, e_k> e_j e_k ) =Sum( <h, e_j> <h, e_k> d_jk )
              = Sum( <h, e_j> <h, e_k>·1) = Sum∣<h, e_j>∣²
    = <h,h> -2·Sum∣<h, e_j>∣² +Sum∣<h, e_j>∣²
    =>   0≤ <h,h> -Sum∣<h, e_j>∣²   , <h,h> = Norm(h)²

zu a)   Der Beweis fußt auf der "Dreiecks-Ungleichung" für Norm(), da der Umweg über ein weiteres Element h˜ länger ist, als der direkte Weg zu S_n:


Folgerung: 
Nach Satz1 Teil(b) gilt für jede geg. orthonormierte Folge e1,e2,... für jedes "n":
    Sum(1→n) ∣<h,e_j>∣² ≤ Norm(h)²
Also ist die Folge der Partialsummen von:
Sum(1→∞) ∣<h,e_j>∣² beschränkt und demzufolge konvergent und man erhält die Ungleichung:
Sum∣<h,e_j>∣² ≤ Norm(h)² , j=1→∞ , Bessel'sche - Ungleichung

Im nachf. Kap. wird nun untersucht, wie man mit Hilfe einer orthonormierten Folge e1,e2,... ein Element h im Sinne der, (durch die von der Norm() erzeugten), Metrik am besten annähern kann.

Def.:   Eine orthonormierte Folge e1,e2,... heißt abgeschlossen in R ,wenn es zu jedem Element h∈R ein n_o und in der lin.Hülle L(e₁,e₂>,...) ein Element h˜_no gibt, so daß bei Vorgabe von ε>0 der Abstand von h zu h˜_no , hier Norm(h-h˜_no) , <ε ist
Bemerkung1:   Diese Def. ist vergleichbar mit dem δ-ε-Kriterium der reellen Zahlen, was nicht verwunderlich ist, da der Eukl.Raum ein Spezialfall des abstr. lin. Raumes mit Skapro() ist.

Bemerkung2:   Die Lin. Komb.'s endlich vieler {e_j} sind laut Axiome ebenfalls Elemente des Raumes R, während die Norm() eine Abbildung der Elemente des Raumes R in die reellen/kompl. Zahlen darstellt.
Wenn also die Normen einer Folge von Elementen (h_j-h) kleiner als eine beliebige Zahl (ε) gemacht werden können, bei entspr. großem Index "n", so ist die Zahlenfolge eine sogenannte "Fundamental-Folge", die bei n->∞ konvergiert, hier zu "h".
Während im Eukl.Raum jede Fundamental-Folge auch konvergiert, muß das im abstr.Raum der Elemente nicht notwendig der Fall sein.

Bemerkung3:   Die Assoziation einer Element-Folge mit einer Fundamental-Folge setzt voraus, daß es genügend orthonormierte Elemente e_j gibt, also unendlich viele.
Als Beispiel sei im Raum der stetigen Funktionen auf einem Intervall (a,b) die orthonormierte Folge:
   {e^i0x, e^i±1x, e^i±2x, ...} genannt,
mit der Norm():
   Norm(e^inx) = <e^inx,e^inx> = ∫e^inx(e^inx)°dx =1
   und:   <e^inx,e^ikx> =d_jk=1 , für j=k, sonst =0
ist {e_n} , n=0,±1, ±2,... eine orthonormierte Folge. Es muß jetzt nur noch die Fundamental-Folgen-Eigenschaft nachgewiesen werden. Es muß also gelten:
∥ h-S_n ∥ →0 , für n->∞   , Beweis folgt weiter unten!

Folgerung:   Nach Satz1, aus Kap.7.9 zuvor, gilt für jedes Element h˜∈L(): Norm(h-S_n) ≤ Norm(h-h˜) , also auch insbesondere für h˜_no:   Norm(h-S_no) ≤ Norm(h-h˜_no)

Bemerkung4:   Bei abgeschlossenen orthonormierten Elementen kann man S_n auch als Partial-Summe von:
Sum(<h ,e_j>e_j) , j->∞ auffassen. Diese Reihe heißt: Fourier-Reihe von "h".
Die Aussage:  Norm(h-S_n) <ε , ∀n≥n_o bedeutet, siehe oben, S_n→h. Dies ist aber zunächst nur eine Konvergenz im Sinne der Metrik (axiomatisch: d(a,b)=Norm(a-b) ).

Satz1:   Ist {e_j} eine abgeschlossene orthonormierte Folge, so gibt es außer h=Null kein weiteres Element mit Skapro(h,e_j)=0
Beweis(indirekt):   Ist <h,e_j>=0 ,∀j ,so ist auch Sum(<h,e_j>e_j>)=0 , j=1...n, n→∞ . Da die S_n→h konvergieren, muß der Grenzwert h auch Null sein, also kann der Satz nur für h=0 richtig sein!   Qed.

Satz2:   Ist {e_j} eine abgeschlossene orthonormierte Folge, dann gilt auch:   Sum∣<h,e_j>∣² = Norm(h)² ,∀h
Beweis:  
Gl.1:   Norm(h-S_n)² =<h-S_n,h-S_n> = <h,h> +<S_n,S_n> - <S_n,h> - <h,S_n>
    <S_n,h> = Sum<h,e_j><e_j,h> =Sum<e_j,h>°<e_j,h> = Sum∣<h,e_j>∣²
    <h,S_n> = <S_n,h>° = (Sum<h,e_j><e_j,h>°) = Sum(<h,e_j><h,e_j>°)°
           = (Sum∣<h,e_j>∣²)° = Sum∣<h,e_j>∣²
In Gl.1 einsetzen:
Gl.2:   Norm(h-S_n)² = ∥h∥² + ∥S_n∥² - 2*Sum∣<h,e_j>∣²
    ∥S_n∥ = <S_n,S_n> = < Sum(<h,e_j>e_j) , Sum(<h,e_k>e_k) >   , wegen: e_j*e_k= δjk folgt:
           =   ( Sum∣<h,e_j>∣² )²     , In Gl.2 einsetzen:
  Norm(h-S_n)² = ∥h∥² - 2*Sum ∣<h,e_j>∣² + ( Sum ∣<h,e_j>∣² )²
=>   Norm(h-S_n)² = ( Norm(h) - Sum ∣<h,e_j>∣² )²
Wenn links S_n→h konvergiert, gilt für rechts:
   Norm(h) - Sum ∣<h,e_j>∣² =0
Ende des Beweises