| 5. Geometr.Objekte im Euklid. Raum, nicht-lin. Abbild. zurück ->4.lin.Abb. |
Ausgangspunkt
Als Erweiterung zum Teil 1 der Analytischen Geometrie wird jetzt ein neues geom.Objekt eingeführt,
die sogenannte "Variablen-Differenz" oder im Grenzübergang zu Null: das "Differential".
Die Differenz Δx ist zunächst nur eine reelle Zahl, aber durch Konstruktion über das
Teilungs-Verhältnis, siehe Abschnitt 4.0c, Teil 1, wird Δx zu einer Strecke mit
Durchlaufsinn, also Richtung, und ist demzufolge entspr. Vorzeichen-behaftet.
Δx= {(P1,P2): P1+t(P2-P1), t: 0->1 } ~(P1,P2) oder:
Δx= {(P1,P2): P1+t(P2-P1), t: 1->0 } ~(P2,P1)
Hat man nun Abbild.f()) einer Quell-Menge zu einer Bild-Menge können Δx-Strecken in Quell- und Bild-Menge über f(), unter bestimmten Anforderungen an f(), in Relation zueinander gesetzt werden: Δyj= f'()*Δxj , j ist Index für den j-ten Unterraum Rj(1)
f'() ist dabei ein von x abhängiger Ausdruck dafür, daß das Verhältnis von Quell- und Bild-Differenz auch im Grenzübergang Δx->0 endl. ist, also einen Grenzwert besitzt.
Dieses konstr.Hilfsmittel ermöglicht es uns, auch nicht lineare Abbild. wie lin.Abbild., siehe Teil 1 "Analyt.Geometrie", zu untersuchen.
Da die Differenzen, wie gesgt, alles reelle Zahlen sind, liegt es nahe, jedem x des Raumes eine entsprechende Differenz (Δx), der Ausdehnung Null, =Differential, zuzuordnen. Dadurch kommt man zu einer weiteren Interpretation des abstr.Eukl.Raumes, mit den gleichen Axiom. Eigenschaften: Linearität, Skalarprodukt, Metrik etc. (Die Untersuchungen zu diesem Aspekt des Eukl.Raumes werden im Teil 6, Analysis vorgenommen)
Beginnen wir mit den Anforderungen an (nicht)-lineare-Abbildungen: f=(f(1),...f(m)).
Δx= {(P1,P2): P1+t(P2-P1), t: 0->1 } ~(P1,P2) oder:
Δx= {(P1,P2): P1+t(P2-P1), t: 1->0 } ~(P2,P1)
Hat man nun Abbild.f()) einer Quell-Menge zu einer Bild-Menge können Δx-Strecken in Quell- und Bild-Menge über f(), unter bestimmten Anforderungen an f(), in Relation zueinander gesetzt werden: Δyj= f'()*Δxj , j ist Index für den j-ten Unterraum Rj(1)
f'() ist dabei ein von x abhängiger Ausdruck dafür, daß das Verhältnis von Quell- und Bild-Differenz auch im Grenzübergang Δx->0 endl. ist, also einen Grenzwert besitzt.
Dieses konstr.Hilfsmittel ermöglicht es uns, auch nicht lineare Abbild. wie lin.Abbild., siehe Teil 1 "Analyt.Geometrie", zu untersuchen.
Da die Differenzen, wie gesgt, alles reelle Zahlen sind, liegt es nahe, jedem x des Raumes eine entsprechende Differenz (Δx), der Ausdehnung Null, =Differential, zuzuordnen. Dadurch kommt man zu einer weiteren Interpretation des abstr.Eukl.Raumes, mit den gleichen Axiom. Eigenschaften: Linearität, Skalarprodukt, Metrik etc. (Die Untersuchungen zu diesem Aspekt des Eukl.Raumes werden im Teil 6, Analysis vorgenommen)
Beginnen wir mit den Anforderungen an (nicht)-lineare-Abbildungen: f=(f(1),...f(m)).
Diese Abhandlung besteht aus folgenden Abschnitten:
5.0
Stetigkeit einer Abbildung ,Abb. =nicht notwendig linear
->5.0
5.1
Beispiele zur Stetigkeit von Abbildungen
->5.1
5.2
Funktion und Wechselwirkung
->5.2
5.3
Funktions-Wert-Berechnung
->5.3
5.4
Differentiale im Rm
->5.4
5.5
Die nicht lineare Abbildung im Rm
->5.5
5.6
Grenzwert-Berechnungen
,Diff. Regeln und Beispiele ->5.6
5.7
Beispiele zum Differenzierungs-Prozeß
->5.7
5.8
Differential-Operator und Umkehrung
->5.8
5.9
Der Integrations-Prozeß I()
->5.9
5.10
Beispiel 'Best.Integral' mittels Ober-/Untersummen- Grenzwert
->5.10
5.11
Approximation von stetigen Funktionen
->5.11
5.0 Stetigkeit einer Abbildung:
Die lin.Abb. hat üblicher Weise die Form eines LGL-Systems. Symb.:
(M)XT=BT .
Wir ersetzen jetzt den Ausdruck: (M)XT durch:
F(X) =(f1(x1,..xm),...,fm(x1,..xm) )
Wenn die f(i)= Lin.Komb. von x1..x(m) sind, hat F(X) die alt-bekannte Matrix-Form.
Allg. wird eine Abbild. in einzelnen Koord. wie folgt geschrieben (b(i)->y(i)):
f1(x1,..xm) = y(1)
f2(x1,..xm) = y(2)
. . . . . . . . . .
fm(x1,..xm) = y(m)
Auch hier wird also ein beliebiger Pkt.P=(x1,x2,...) in einen Bild-punkt P'(y1,y2,..) transformiert. x(i) und y(i) sind jeweils reelle Zahlen, die {f(j)} repräsentieren demzufolge, wie die Lin.Komb. L(j) bei lin. Abb., eine allg.Abbildung aus dem Rm in den R'm .
Bemerkung1: Sind alle f(i) lin.Komb., brauchten wir uns keine Gedanken über die Art der L() zu machen, weil laut Axiomatik des Eukl.Raumes der Bild-Punkt P' durch L(p1,..p(m))=P' (lin.Komb.) ebenfalls automatisch zum Raum gehört.
Bei f(i) ist das anders. Hier müssen gewisse Anforderungen an f(i) gestellt werden, damit etwas sinnvolles herauskommt, nämlich zumindest die Zugehörigkeit des Bild-Elementes P', fi(p1,..p(m))=P', zum Raum, also:
P'∈Rm .
Dies beinhaltet auch, dass P' in keiner Koord. unendl. sein darf!
Bemerkung2: Aus Bemerkung 1 geht hervor, dass die f(i) so beschaffen sein müssen, daß die Bildpunkte genauso "dicht" liegen, wie die Quellpunkte. Was bedeutet das:
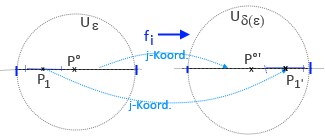
Def.1 δ-Umgebung: Wird eine delta-Umg. um P1 zu einer entspr. delta-Umg. um Bildpunkt fi(P1) abgebildet, d.h. Ausdehnung der Bild-delta-Umg. beschränkt, so werden Quell- und Ziel-Umg. wie folgt bezeichnet:
Quelle: P°∈Rm, ε>0 => {(x(1),..): abs(x(j)-p°(j))<ε }
Quelle ist also m-dim Intervall um P°
Ziel: P°'=fi(P°), δε>0 => {(y(1),..): abs(y(j)-p°'(j))<δε }
Ziel ist auch m-dim Intervall, jetzt aber um P°', die Ausdehnung ist hier
entspr. abhängig von der Quell-Ausdehnung.
Symb. spricht man in diesem Fall, bei Beziehungen zwischen Quell-und Ziel-Mengen, von einem sog. "δ-ε" -Kriterium.
Def.2 Stetigkeit fi : Uε1 sei Umgebung zu einem weiteren Pkt.P1 innerhalb der epsilon-Umg.(P°) und liegt die Bild-Umg. Uδ(ε1)(P1') auch innerhalb der Bild-Umg. Uδ(ε)(P°'), dann heißt fi stetig in der Umgebung des Punktes P°(i) .
Bild , Anal2-geo1.jpg
Len/Len'<1 :Vergröß. der Ziel-Länge
Len/Len'>1 :Verklein. der Ziel-Länge
Len/Len'=1 :keine Veränd.Quell=Ziel
Hierbei müssen natürlich Len und Len' ≠0 sein.
Nachfolgend einige Beispiele von stetigen Abbildungen.
F(X) =(f1(x1,..xm),...,fm(x1,..xm) )
Wenn die f(i)= Lin.Komb. von x1..x(m) sind, hat F(X) die alt-bekannte Matrix-Form.
Allg. wird eine Abbild. in einzelnen Koord. wie folgt geschrieben (b(i)->y(i)):
f1(x1,..xm) = y(1)
f2(x1,..xm) = y(2)
. . . . . . . . . .
fm(x1,..xm) = y(m)
Auch hier wird also ein beliebiger Pkt.P=(x1,x2,...) in einen Bild-punkt P'(y1,y2,..) transformiert. x(i) und y(i) sind jeweils reelle Zahlen, die {f(j)} repräsentieren demzufolge, wie die Lin.Komb. L(j) bei lin. Abb., eine allg.Abbildung aus dem Rm in den R'm .
Bemerkung1: Sind alle f(i) lin.Komb., brauchten wir uns keine Gedanken über die Art der L() zu machen, weil laut Axiomatik des Eukl.Raumes der Bild-Punkt P' durch L(p1,..p(m))=P' (lin.Komb.) ebenfalls automatisch zum Raum gehört.
Bei f(i) ist das anders. Hier müssen gewisse Anforderungen an f(i) gestellt werden, damit etwas sinnvolles herauskommt, nämlich zumindest die Zugehörigkeit des Bild-Elementes P', fi(p1,..p(m))=P', zum Raum, also:
Dies beinhaltet auch, dass P' in keiner Koord. unendl. sein darf!
Bemerkung2: Aus Bemerkung 1 geht hervor, dass die f(i) so beschaffen sein müssen, daß die Bildpunkte genauso "dicht" liegen, wie die Quellpunkte. Was bedeutet das:
Def.1 δ-Umgebung: Wird eine delta-Umg. um P1 zu einer entspr. delta-Umg. um Bildpunkt fi(P1) abgebildet, d.h. Ausdehnung der Bild-delta-Umg. beschränkt, so werden Quell- und Ziel-Umg. wie folgt bezeichnet:
Quelle: P°∈Rm, ε>0 => {(x(1),..): abs(x(j)-p°(j))<ε }
Ziel: P°'=fi(P°), δε>0 => {(y(1),..): abs(y(j)-p°'(j))<δε }
Symb. spricht man in diesem Fall, bei Beziehungen zwischen Quell-und Ziel-Mengen, von einem sog. "δ-ε" -Kriterium.
Def.2 Stetigkeit fi : Uε1 sei Umgebung zu einem weiteren Pkt.P1 innerhalb der epsilon-Umg.(P°) und liegt die Bild-Umg. Uδ(ε1)(P1') auch innerhalb der Bild-Umg. Uδ(ε)(P°'), dann heißt fi stetig in der Umgebung des Punktes P°(i) .

Len/Len'>1 :Verklein. der Ziel-Länge
Len/Len'=1 :keine Veränd.Quell=Ziel
Nachfolgend einige Beispiele von stetigen Abbildungen.
5.1 Beispiele: Stetigkeit von Abb.:
Beispiel1 Lineare Abb.:
Die lin.Abb. wird innerhalb einer Koord. untersucht. Die Quell-Var. wird mit x bezeichnet, das Bild mit y:
M: {(x,y): Ax+By+C=0, A,B,C reelle Konst.}
Auflösung nach y: y=f(x) = -A/B *x -C ,oder
Auflösung nach x: x=g(y) = -B/A *y -C
y=f(g(y))= -A/B *(-B/A *y -C) -C = 1y
=> y/y =f(g(y)) =1f,g sind zueinander inverse Abbild.
Nun bezeichnen wir beliebige Intervalle mit Δx und Δy in den jeweiligen Quell- und Bildmengen. Dann gelten die Relationen:
Δx =-B/A*Δy und Δy =-A/B*Δx, C fällt bei Diff.-Bildung weg
Man erkennt sofort, dass der Quotient Δx/Δy und umgekehrt überall gleich, nämlich konstant= -A/B o. -B/A ist.
Beispiel: 3x +2y +C =0
Bild , Anal2-geo2.jpg
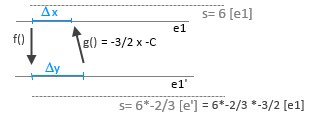
Aus Δy=-3/2*Δx folgt das Teilungsverhältnis:
Δx/Δy = -2/3 => Δx*3 +Δy*2 =0 das Gleichgewichts-Prinzip zweier Richtungen, die zueinander im Gleichgewicht stehen, siehe: Analyt.Geo.II, 4.0c Teilungsverhältnis u. Arithmetisches Mittel .
Beispiel2 nicht-lin. Abb.:
M: {(x,y): y*(x-C)-1=0, C reelle Konst.}
Die Auflösung nach y lautet:
y=f(x)= 1/(x-C) , Seien {C+x/n}, n=1,2... Quellpunkte,
dann sind y(n) = 1/(C +1/n -C) =n Zielpunkte.
Die Differenzen y(n)-y(m) = 1/n-1/m =(m-n)/n*m gehen für große n,m ->0, aber der Grenzwert y(n) ist: Lim(y(n))=∞. Die Abb. f ist im Punkt x=C demzufolge nicht mehr stetig nach Def.2 Abschnitt 5.0
Dadurch kann man auch das Paar Δx<->Δy nur rechts o. links von x=C bilden mit einem gewissen Abstand zu C. In der Nähe zu C werden die Qotienten Δx/Δy und umgekehrt immer größer, je näher man an C heran kommt.
Abbildung in offenem Intervall M:
Jedes Element(Zahl) innerhalb M, welches in ein Bild-Element abbgebildet wird, ist laut Aussage im Abschnitt: 3.4 Sätze über konvergente Folgen, Modell der reellen Zahlen gleichzeitig Grenzwert von Fundamentalfolgen, deren Elemente natürlich auch abgebildet werden.
Man muß nun 2 Fälle unterscheiden, danach, ob der Grenzwert(G) ebenfalls in M liegt, oder nicht. Liegt G nicht in M dann kann er nur auf dem Rand von M liegen, da der Rand einerseits nicht zu M gehört, anderseits aber dicht genug an den {x(n)} für genügend große Indizes "n" (δ , nδ -Kriterium).
1. G∈M :
In diesem Fall kann man G als Max. der Grenzwerte aller Fundamentalfolgen in M betrachten, deren Grenzwerte in M liegen. M' ist dann eine Menge wie folgt:
M'= {x: d(x-G)≤G<ε ,x=sign(x)x, G=sign(G)G }
Dies ist aber die Def. einer kompakten Menge, die von unendlich vielen off. Umgeb., nämlich von den Uδ(x(n)), n=1,2,.. , überdeckt wird.
Nach Satz von Heine-Borel, siehe Abschnitt 3.11, Satz4, genügen zur Überdeckung aber bereits endl. viele Umgeb..
Da die Ausdehnung der Bildmenge ≤Summe aller abgebildeten Teilmengen von M' ist, und die Bildmengen nach Stetigkeits-Voraussetzung selbst eine Ausdehnung <δε haben, ist die endl.Summe endl.Ausdehnung selbst endlich, also beschränkt.
2. G nicht in M :
In diesem Fall kann die Funktion nach Beispiel 2 zuvor unendlich sein.
Folgerung:
Aus umgekehrter Betrachtung im Fall 1. zuvor folgt die wohl wichtigste Aussage in der Abbildungs-Theorie:
Satz:(nach Bolzano /Weierstraß)
Eine stetige Funktion auf kompakter Menge ist beschränkt.
Folgerung:
Ist die ε-Umgebung der gesamte Raum, dann ist die zugehörige stetige Funktion im gesamten Bildraum beschränkt, und kann höchstens im Unendlichen unendlich sein. Beispiel f=exp(x):
Lim[f(x)]=0 für x->-∞ und Lim[f(x)]=∞ für x->∞ ,
=> abs(exp(x))≤kx für abs(x)≤k<∞
Die lin.Abb. wird innerhalb einer Koord. untersucht. Die Quell-Var. wird mit x bezeichnet, das Bild mit y:
Auflösung nach y: y=f(x) = -A/B *x -C ,oder
Auflösung nach x: x=g(y) = -B/A *y -C
y=f(g(y))= -A/B *(-B/A *y -C) -C = 1y
=> y/y =f(g(y)) =1
Nun bezeichnen wir beliebige Intervalle mit Δx und Δy in den jeweiligen Quell- und Bildmengen. Dann gelten die Relationen:
Δx =-B/A*Δy und Δy =-A/B*Δx
Man erkennt sofort, dass der Quotient Δx/Δy und umgekehrt überall gleich, nämlich konstant= -A/B o. -B/A ist.
Beispiel: 3x +2y +C =0
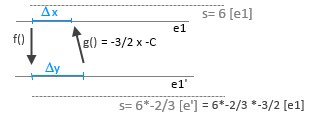
Aus Δy=-3/2*Δx folgt das Teilungsverhältnis:
Δx/Δy = -2/3 => Δx*3 +Δy*2 =0 das Gleichgewichts-Prinzip zweier Richtungen, die zueinander im Gleichgewicht stehen, siehe: Analyt.Geo.II, 4.0c Teilungsverhältnis u. Arithmetisches Mittel .
Beispiel2 nicht-lin. Abb.:
Die Auflösung nach y lautet:
y=f(x)= 1/(x-C) , Seien {C+x/n}, n=1,2... Quellpunkte,
dann sind y(n) = 1/(C +1/n -C) =n Zielpunkte.
Die Differenzen y(n)-y(m) = 1/n-1/m =(m-n)/n*m gehen für große n,m ->0, aber der Grenzwert y(n) ist: Lim(y(n))=∞. Die Abb. f ist im Punkt x=C demzufolge nicht mehr stetig nach Def.2 Abschnitt 5.0
Dadurch kann man auch das Paar Δx<->Δy nur rechts o. links von x=C bilden mit einem gewissen Abstand zu C. In der Nähe zu C werden die Qotienten Δx/Δy und umgekehrt immer größer, je näher man an C heran kommt.
Abbildung in offenem Intervall M:
Jedes Element(Zahl) innerhalb M, welches in ein Bild-Element abbgebildet wird, ist laut Aussage im Abschnitt: 3.4 Sätze über konvergente Folgen, Modell der reellen Zahlen gleichzeitig Grenzwert von Fundamentalfolgen, deren Elemente natürlich auch abgebildet werden.
Man muß nun 2 Fälle unterscheiden, danach, ob der Grenzwert(G) ebenfalls in M liegt, oder nicht. Liegt G nicht in M dann kann er nur auf dem Rand von M liegen, da der Rand einerseits nicht zu M gehört, anderseits aber dicht genug an den {x(n)} für genügend große Indizes "n" (δ , nδ -Kriterium).
1. G∈M :
In diesem Fall kann man G als Max. der Grenzwerte aller Fundamentalfolgen in M betrachten, deren Grenzwerte in M liegen. M' ist dann eine Menge wie folgt:
M'= {x: d(x-G)≤G<ε ,x=sign(x)x, G=sign(G)G }
Dies ist aber die Def. einer kompakten Menge, die von unendlich vielen off. Umgeb., nämlich von den Uδ(x(n)), n=1,2,.. , überdeckt wird.
Nach Satz von Heine-Borel, siehe Abschnitt 3.11, Satz4, genügen zur Überdeckung aber bereits endl. viele Umgeb..
Da die Ausdehnung der Bildmenge ≤Summe aller abgebildeten Teilmengen von M' ist, und die Bildmengen nach Stetigkeits-Voraussetzung selbst eine Ausdehnung <δε haben, ist die endl.Summe endl.Ausdehnung selbst endlich, also beschränkt.
2. G nicht in M :
In diesem Fall kann die Funktion nach Beispiel 2 zuvor unendlich sein.
Folgerung:
Aus umgekehrter Betrachtung im Fall 1. zuvor folgt die wohl wichtigste Aussage in der Abbildungs-Theorie:
Satz:
Eine stetige Funktion auf kompakter Menge ist beschränkt.
Folgerung:
Ist die ε-Umgebung der gesamte Raum, dann ist die zugehörige stetige Funktion im gesamten Bildraum beschränkt, und kann höchstens im Unendlichen unendlich sein. Beispiel f=exp(x):
Lim[f(x)]=0 für x->-∞ und Lim[f(x)]=∞ für x->∞ ,
=> abs(exp(x))≤kx für abs(x)≤k<∞
5.2 Funktion und Wechselwirkung:
Die Funktion ist eine Zuordnungsvorschrift, die jeder Zahl eine andere Zahl,
möglichst nur eine, zuordnet. Dabei ist die Zuordnung eine Folge von elementaren
bis komplexen math. Verknüpfungen, wie Add/Sub, Math/Div etc., also alle im Eukl.
Raum zulässigen Operationen.
Der Begriff "Folge" impliziert in der Axiomatik das sogenannte "Endlichkeits-Prinzip":
1.: Jedem Element einer Folge von Zahlen wird mittels einer endl.Folge von Anweisungen eine andere Zahl zugeordnet.
Diese Form wird als diskrete Funktion einer diskreten Variablen (einzelne Zahlen) bezeichnet. Die Punkte der Quell- und Ziel-Menge liegen isoliert, d.h., zwischen 2 Zahlen hat eine ganze δ-Umgeb. platz, was bedeutet:
d(x(i) -x(i+1))>0 und d(f(x(i)) -f(x(i+1)))>0.
Anwendung: Werte-Tabellen, Ereignislisten usw.
Bemerkung: Die endl.Folge von Anweisungen kann durch das Prinzip der vollst.Induktion ins Unendliche ausgeweitet werden. Zumindest die Anweisungsfolge für den Schluss von n nach n+1 muß aber endl. sein.
Soweit es sich um "Unendlichkeit" handelt, kann dann auf die gesamte Folge nur noch über einen Namen zugegriffen werden.
Beispiel: unendl. Potenzreihe: z.B. exp()-Funktion,
Irrationaler Quotient aus Keis-Durchmesser(d) und Umfang(k): d*k/d =pi, (pi steht für eine unendl.Ziffernfolge: 3.14159...)
2.: Zuordnungsvorschrift für eine unendl. Menge reeller Zahlen = Intervall reell. Zahlen. Auf dieses kann man als Ganzes nur über einen Namen, z.B. x=reell, und einer Einschränkung, z.B. a<x<b, zugreifen.
Die Zuordn.Vorschrift beinhaltet dann auch nur noch den Namen "x" und nicht die einzelne Zahl.
Folgerung:
In den konkreten Anwendungen, z.B. Funktionswert-Berechnungen, können wegen des Endl.-Prinzip, nur rationale Zahlen, als explizite Zeichenfolge, oder Namen zum Rechnen, Eingeben, Ausdrucken, Aufschreiben, Lesen, usw. verwendet werden.
Konstruktion v. stetig.Funktionen:
1.: Durch Verbinden von Bildpunkten, z.B. mit Geraden, kann leicht eine stetige Funktion zu einer diskreten Variablen hergestellt werden.
2.: Alle Verknüpfungen, endl. o. unendl., lassen sich auf Verknüpfungen von Potenzreihen zurückführen, weil laut "3. Modell der reellen Zahlen" jede Zahl gleichzeitig Grenzwert beliebiger, aber geeigneter, Potenzreihen ist.
Satz: Die Potenzreihe ist auf kompakten Mengen stetig, bis auf eine max. abzählbare Menge von isolierten Punkten.
a) Die einfachste Funktion ist: y=f(x)=const.
Hier findet zwischen Quell und Ziel keine Wechselwirkung statt. (Im Newton-Raum existiert nur das Prinzip der relativen Ruhe o. Konstanz in einem zugehörigen Inert-System)
b) y=f(x)=x , das ist die sogenannte identische Funktion. Sie bildet jede δ-Umgeb. in die gleiche δ-Umgeb. zum gleichen Punkt ab.
Stellt man Quell- und Ziel-Raum in einer Grafik gegenüber, so erhält man eine Diagonale durch Null mit der Eigenschaft, daß jeder Punkt der Diagonale den gleichen Abstand zur x-Achse (Quelle) und y-Achse (Ziel) hat.
Die identische Funktion ist die einzige Funktion bei der die inverse Funktion gleich der Funktion ist. y=x, x=y.
c) Lineare Funktion: Ax +By +C=0 , hatten wir bereits zuvor ausführlich behandelt.
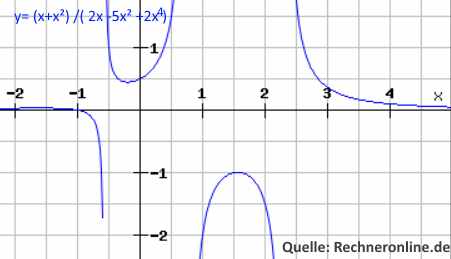
d) Polynom/Polynom =Rationale Funktion.
Polynom: a1*x +a2*x² + . . .+ a(n)*xn
Die rat.Funktion besitzt i.a. n-Unstetigkeits-Stellen =Nullstellen des Nenner-Polynoms. Beispiel: f(x)= (x +x²)/(2x -5x² +2x4)
Bild , Anal2-geo4.jpg
e) Transzendente Funktionen, allg. y=Potenzreihe(x), Beispiel:
Bild , Anal2-geo3.jpg
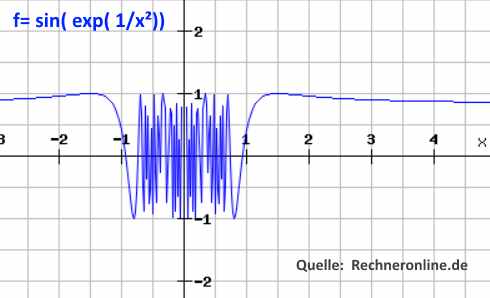
f) Quadratische Formen: lin(x,y)²:
(Ax +By +C)² =0 oder Ax² +By² +Cxy +Dx +Ey +F =0
werden weiter unten behandelt.
1.: Jedem Element einer Folge von Zahlen wird mittels einer endl.Folge von Anweisungen eine andere Zahl zugeordnet.
Diese Form wird als diskrete Funktion einer diskreten Variablen (einzelne Zahlen) bezeichnet. Die Punkte der Quell- und Ziel-Menge liegen isoliert, d.h., zwischen 2 Zahlen hat eine ganze δ-Umgeb. platz, was bedeutet:
d(x(i) -x(i+1))>0 und d(f(x(i)) -f(x(i+1)))>0.
Anwendung: Werte-Tabellen, Ereignislisten usw.
Bemerkung: Die endl.Folge von Anweisungen kann durch das Prinzip der vollst.Induktion ins Unendliche ausgeweitet werden. Zumindest die Anweisungsfolge für den Schluss von n nach n+1 muß aber endl. sein.
Soweit es sich um "Unendlichkeit" handelt, kann dann auf die gesamte Folge nur noch über einen Namen zugegriffen werden.
Beispiel: unendl. Potenzreihe: z.B. exp()-Funktion,
Irrationaler Quotient aus Keis-Durchmesser(d) und Umfang(k): d*k/d =pi, (pi steht für eine unendl.Ziffernfolge: 3.14159...)
2.: Zuordnungsvorschrift für eine unendl. Menge reeller Zahlen = Intervall reell. Zahlen. Auf dieses kann man als Ganzes nur über einen Namen, z.B. x=reell, und einer Einschränkung, z.B. a<x<b, zugreifen.
Die Zuordn.Vorschrift beinhaltet dann auch nur noch den Namen "x" und nicht die einzelne Zahl.
Folgerung:
In den konkreten Anwendungen, z.B. Funktionswert-Berechnungen, können wegen des Endl.-Prinzip, nur rationale Zahlen, als explizite Zeichenfolge, oder Namen zum Rechnen, Eingeben, Ausdrucken, Aufschreiben, Lesen, usw. verwendet werden.
Konstruktion v. stetig.Funktionen:
1.: Durch Verbinden von Bildpunkten, z.B. mit Geraden, kann leicht eine stetige Funktion zu einer diskreten Variablen hergestellt werden.
2.: Alle Verknüpfungen, endl. o. unendl., lassen sich auf Verknüpfungen von Potenzreihen zurückführen, weil laut "3. Modell der reellen Zahlen" jede Zahl gleichzeitig Grenzwert beliebiger, aber geeigneter, Potenzreihen ist.
Satz: Die Potenzreihe ist auf kompakten Mengen stetig, bis auf eine max. abzählbare Menge von isolierten Punkten.
a) Die einfachste Funktion ist: y=f(x)=const.
Hier findet zwischen Quell und Ziel keine Wechselwirkung statt. (Im Newton-Raum existiert nur das Prinzip der relativen Ruhe o. Konstanz in einem zugehörigen Inert-System)
b) y=f(x)=x , das ist die sogenannte identische Funktion. Sie bildet jede δ-Umgeb. in die gleiche δ-Umgeb. zum gleichen Punkt ab.
Stellt man Quell- und Ziel-Raum in einer Grafik gegenüber, so erhält man eine Diagonale durch Null mit der Eigenschaft, daß jeder Punkt der Diagonale den gleichen Abstand zur x-Achse (Quelle) und y-Achse (Ziel) hat.
Die identische Funktion ist die einzige Funktion bei der die inverse Funktion gleich der Funktion ist. y=x, x=y.
c) Lineare Funktion: Ax +By +C=0 , hatten wir bereits zuvor ausführlich behandelt.
d) Polynom/Polynom =Rationale Funktion.
Polynom: a1*x +a2*x² + . . .+ a(n)*xn
Die rat.Funktion besitzt i.a. n-Unstetigkeits-Stellen =Nullstellen des Nenner-Polynoms. Beispiel: f(x)= (x +x²)/(2x -5x² +2x4)

e) Transzendente Funktionen, allg. y=Potenzreihe(x), Beispiel:

f) Quadratische Formen: lin(x,y)²:
(Ax +By +C)² =0 oder Ax² +By² +Cxy +Dx +Ey +F =0
werden weiter unten behandelt.
Funktionswert-Berechnungen:
5.3
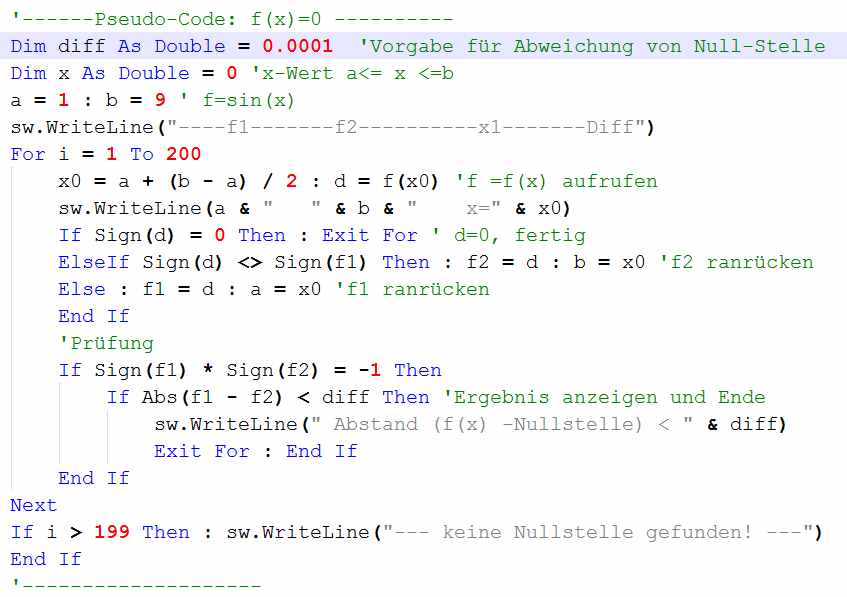
Häufig vorkommendes Problem bei stetigen Funktionen: Die Null-Stellen-Berechnung:
Nachfolgend ein Listing für ein Halbierungs-Verfahren zur Null-Stellen-Berechnung:
Bild , Anal2-geo5.jpg
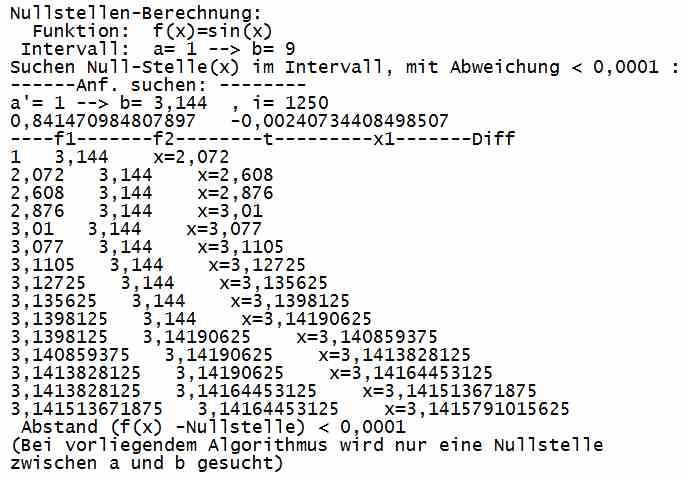
Zu vorigem Listing ein durchgerechnetes Beispiel für Nullstelle von sin(x) im Intervall 1≤x≤9 :
Bild , Anal2-geo6.jpg
Nachfolgend ein Listing für ein Halbierungs-Verfahren zur Null-Stellen-Berechnung:

Zu vorigem Listing ein durchgerechnetes Beispiel für Nullstelle von sin(x) im Intervall 1≤x≤9 :

5.4 Differentiale im Rm
Differentiale sind Punkt-Differenzen (relle Zahl) in den 1-dim Quell- und Bild-Unterräumen
einer beliebigen Abbild. Im Punkt 5.0 zuvor hatten wir zu einer stetigen Funktion f() die
Quell-und Ziel- ε/δ(ε)-Umgebung def. In diesen 2 miteinander
über f() verbund. Mengen kann man Teilmengen wie folgt def:
Δx={(P1,P2): P1+t*(P2-P1),0≤t≤1 ,P1,P2∈Uε}
Interpretation: Wir haben es hier mit einer Verbind.Linie zwischen 2 Punkten, hier im Intervall sind Pkte. Zahlen, zu tun. Grenwert bilden:
für t->0 ist Lim(Δx) eine Strecke der Ausdehnung Null im Punkt P1. Da P1 für jeden beliebigen Pkt. in Quelle steht, schreiben wir im Grenzfall: Δx -> δx
Im Bild-Raum ähnlich y=f(x):
Δy -> δy oder Δf() -> δf
Bis jetzt stehen die so gebildete Diff. allein für sich, d.h. unabhängig von eienander.
1.: Eigenschaften der spez. Diff. Δx / f(Δx):
Δx={(P1,P2): P1+t*(P2-P1),0≤t≤1 }
Δ'x={(P1,P2): P1-t*(P2-P1),0≤t≤1 }
Δ'x und Δx sind Intervalle rts. und lks vom Pkt.P1.
Durch die Stetigkeit von f() ist gewährleistet, daß f(Δx) ebenfalls ein enspr. Intervall im Bild ist. Man kann nun folg. Grenzübergänge (t->0) vornehmen:
lim( Δf(x)/Δx ) = relle Zahl a und:
lim( Δf(x)/Δ'x ) = relle Zahl á
Satz: Existieren beide Grenzwerte a,á und gilt a=á ,dann heißt der so gebildete Quotient: Differential-Quotient der Abb. f() im Pkt. P1 ,respektive Pkt.x (x=P1),
Symb.: dy/dx o. df(x)/dx in jedem Pkt. x∈Uε
Bemerkung1:
Es sind auch kürzere Schreibweisen üblich:
Dxf oder f'=f'(x) ,f' ="Ableitung", wird hier als eigenständige Funktion von x aufgefaßt, wie f(x).
Dxf müßte dann noch gesondert auf Stetigkeit untersucht werden.
Bemerkung2:
Den vorgegebenen Funktionen f() sieht man i.a. natürlich nicht an, ob die Grenzwerte existieren. Es bedarf sorgfältiger Untersuchungen und einen ganzen Wissenschafts-Zweig, der sich nur mit Differentiations-Regeln und Bildung von Ableitungen (-Funktionen) beschäftigt.
Grundsätzlich kann man aber sagen, Ableitungen existieren nicht:
- In Unstetigkeits-Punkten
- In Spitzen, Ecken, Kanten, z.B. wenn diskrete Funkt. mit Geraden verbunden werden
- keine δ-Umgeb. rts. o.lks vom Bild.Pkt. vorhanden ist
Umgekehrt ist Differenzierbarkeit vorhanden, wenn der Funktions-Graph optisch glatt oder harmonisch geschwungen aussieht. Dies ist bei allen Funktionen im Abschnitt 5.2 ,2.Satz a)-f) gegeben (bis auf isolierte Pkte.).
2.: Differentiale in mehreren Unterräumen R1:
Bis jetzt hatten wir eine Koord. (Unterraum) herausgegriffen und dx,dy gebildet. Für alle Koord. ergeben sich aus der Stetigkeits-Def. im Normalfall m-verschiedene δ-Umgebungen:
ε1, . . , εm .Um für f(x1,x2,...) eine einheitliche Umgebung zu bekommen bilden wir gesamt-ε:
ε =sqrt(ε1²+...+εm²)
Die Projektionen einer Verbindungs-Linie (P1,P2) liegen dann ebenfalls in den enstrpr. Bild-Unterräumen.
Beispiel für i,j -Unterraum:
Bild , Anal2-geo7.jpg
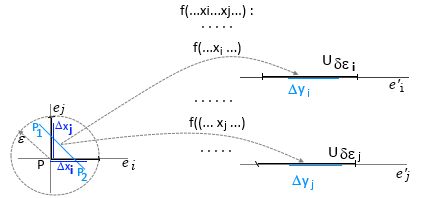
dfi,j = f(..dx(i)...dx(j)...) = f(..dx(i)..) +f(..dx(j)..)
3.: Relation zwischen Quell- und Bild-Diff. :
dx und df sind Richtungen deren Quotient beim Grenzübergang eine feste Zahl darstellt, (an dem Punkt, wo er gebildet wurde), und demzufolge wie beim Dreieck ein "Winkel-Maß" def.
Bild , Anal2-geo8.jpg
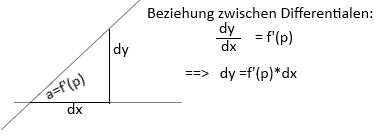
dfi,j(p) = df(i) +df(j)
= Dif(p)*dx(i) +Djf(p)*dx(j)
Es gibt auch eine gesamt-Darstellung der Diff. für alle Unterräume:
df= D1f()*dx(1) +D2f()*dx(2) + . . .
Diese Darstellung hat die Form einer Linear-Komb. und kann deshalb als lin.-Abb. weiter untersucht werden.
Δx=
Interpretation: Wir haben es hier mit einer Verbind.Linie zwischen 2 Punkten, hier im Intervall sind Pkte. Zahlen, zu tun. Grenwert bilden:
für t->0 ist Lim(Δx) eine Strecke der Ausdehnung Null im Punkt P1. Da P1 für jeden beliebigen Pkt. in Quelle steht, schreiben wir im Grenzfall: Δx -> δx
Im Bild-Raum ähnlich y=f(x):
Δy -> δy oder Δf() -> δf
Bis jetzt stehen die so gebildete Diff. allein für sich, d.h. unabhängig von eienander.
1.: Eigenschaften der spez. Diff. Δx / f(Δx):
Δx=
Δ'x=
Δ'x und Δx sind Intervalle rts. und lks vom Pkt.P1.
Durch die Stetigkeit von f() ist gewährleistet, daß f(Δx) ebenfalls ein enspr. Intervall im Bild ist. Man kann nun folg. Grenzübergänge (t->0) vornehmen:
lim( Δf(x)/Δx ) = relle Zahl a und:
lim( Δf(x)/Δ'x ) = relle Zahl á
Satz: Existieren beide Grenzwerte a,á und gilt a=á ,dann heißt der so gebildete Quotient: Differential-Quotient der Abb. f() im Pkt. P1 ,respektive Pkt.x (x=P1),
Symb.: dy/dx o. df(x)/dx
Bemerkung1:
Dxf oder f'=f'(x) ,f' ="Ableitung", wird hier als eigenständige Funktion von x aufgefaßt, wie f(x).
Dxf müßte dann noch gesondert auf Stetigkeit untersucht werden.
Bemerkung2:
Den vorgegebenen Funktionen f() sieht man i.a. natürlich nicht an, ob die Grenzwerte existieren. Es bedarf sorgfältiger Untersuchungen und einen ganzen Wissenschafts-Zweig, der sich nur mit Differentiations-Regeln und Bildung von Ableitungen (-Funktionen) beschäftigt.
Grundsätzlich kann man aber sagen, Ableitungen existieren nicht:
- In Unstetigkeits-Punkten
- In Spitzen, Ecken, Kanten, z.B. wenn diskrete Funkt. mit Geraden verbunden werden
- keine δ-Umgeb. rts. o.lks vom Bild.Pkt. vorhanden ist
Umgekehrt ist Differenzierbarkeit vorhanden, wenn der Funktions-Graph optisch glatt oder harmonisch geschwungen aussieht. Dies ist bei allen Funktionen im Abschnitt 5.2 ,2.Satz a)-f) gegeben (bis auf isolierte Pkte.).
2.: Differentiale in mehreren Unterräumen R1:
Bis jetzt hatten wir eine Koord. (Unterraum) herausgegriffen und dx,dy gebildet. Für alle Koord. ergeben sich aus der Stetigkeits-Def. im Normalfall m-verschiedene δ-Umgebungen:
ε1, . . , εm .Um für f(x1,x2,...) eine einheitliche Umgebung zu bekommen bilden wir gesamt-ε:
ε =sqrt(ε1²+...+εm²)
Die Projektionen einer Verbindungs-Linie (P1,P2) liegen dann ebenfalls in den enstrpr. Bild-Unterräumen.
Beispiel für i,j -Unterraum:

dfi,j = f(..dx(i)...dx(j)...) = f(..dx(i)..) +f(..dx(j)..)
3.: Relation zwischen Quell- und Bild-Diff. :
dx und df sind Richtungen deren Quotient beim Grenzübergang eine feste Zahl darstellt, (an dem Punkt, wo er gebildet wurde), und demzufolge wie beim Dreieck ein "Winkel-Maß" def.

= Dif(p)*dx(i) +Djf(p)*dx(j)
Es gibt auch eine gesamt-Darstellung der Diff. für alle Unterräume:
Diese Darstellung hat die Form einer Linear-Komb. und kann deshalb als lin.-Abb. weiter untersucht werden.
5.5 Die (nicht) lineare Abbildung im Rm
Das Wort "nicht" habe ich ausgeklammert, weil wir später erkennen
werden, daß nachfolg. Überlegungen auch für lineare Abbild. gelten.
{fi(x1,x2,...) =yi }, i=1...m , definiert.
Die Quell- und Bild-Variablen werden jetzt als Richtung/Vektor aufgefaßt:
(x1,x2,...)=X und (y1,y2,...)=Y
Gegenüber LGL-Systemen, die überall im Raum stetig sind, muß man hier, an beliebige Funktionen, Mindest-Anforderungen für die Bearbeitung stellen:
1. Quell-Menge M={ d(X-P)<ε , ε>0 }
2.
3.
Dann können wir die Differentiale in Quell und Bild bilden:
df(1): D1f1(X)*x1 +... +Dmf1(X)*x(m) =dy(1)
df(2): D1f2(X)*x1 +... +Dmf2(X)*x(m) =dy(2)
. . . . . . .
df(m): D1fm(X)*x1 +... +Dmfm(X)*x(m) =dy(m)
Wir haben also ein n,m Gleich.System, mit n=m, für die Beschreibung wie die m-Richtungen der Quelle: dX in die m-Bild-Richt: dY transformiert werden.
dX=(dx1,dx2,...) ,dY=(dy1,dy2,...) sind Vektoren wie X und Y.
Die Gleich. haben die Form wie Lin.Komb. bei Lin.Abbild., deshalb ziehen wir die Koeff. zu einer eigenen Matrix (F) heraus:
F:
( D1f1(X) . . . . Dmf1(X) )
( D1f2(X) . . . . Dmf2(X) )
. . . . . . . .
( D1fm(X) . . . . Dmfm(X) )
Symb: Djfi(X) =δfi(X)/δxj ,=part.Diff.Quotient
Unter diesen Voraussetzungen können wir jetzt def.:
Definition: Die allg. (nicht)-lineare Abbildung hat die Form einer linearen Abbildung zwischen ihren Diff: F*dX=dY
Bemerkung: Die Bild-Differentiale sind Richtungen im Bild-Raum wie die 'dx(j)' in M, beide der Ausdehnung Null. Der Unterschied ist nur, die dx(j) haben in M überall die gleichen Winkel zueinander, d.h. das Vol(dx1dx2***dxm) ist überall der gleiche m-dim 0-Würfel mit dem gleichen Volumen=const. Demgegenüber bilden die Richtungen dx(j) zumindest ein 0-Spat im Bild-Raum, aber jetzt ist die Geometrie des Spates und dessen Inhalt an jedem Punkt in Bild(M) verschieden.
Ähnlich wie bei den lin.Matrizen kann man das Volumen-Verhältnis zwischen Quell-Spat und Bild-Spat durch die Determinante der F-Matrix bestimmen:
Det(F) =Funktional-Determinante des Funkt.-System f=(f1,f2,..) an einem beliebigen Punkt P in M.
Symb: Det(F) =δ(f1...fm) /δ(x1...xm)
Beispiel:
Matrix M:
( 5 3 )
(-2 1 )
Daraus folgt:
f1: 5x1 +3x2
f2: -2x1 +1x2
Matrix F:
D1f1(x1,x2) =5 , D2f1(x1,x2) =3
D1f2(x1,x2) =-2 , D2f2(x1,x2) =1
Matrix F =Matrix M
d.h., bei lin.Abb. entartet die Funktional-Determinante zu einer reellen Konstante im gesamten Raum!
(Die dx1,dx2... respektive dy1,dy2,.. können hier durch x1,x2,.. und y1,y2,.. ersetzt werden, weil man sich die Diff.-Richtungen zu Koord.Achsen verlängert denken kann.)
Beispiel:
M={(x,y): G()=Ax²+By²+Cxy +Dx +Ey +F =0 }
Die Funktion G() bildet zunächst eine Pkt.-Menge{x,y} der Ebene in die reellen Zahlen{z} ab. In einem 3-dim Koord.System würde dann z ,als 3.Koord. über x,y-Ebene, eine Pkt.Menge in Form einer gekrümmten Fläche {x,y,G()} ergeben. Mittels G()=0 wird die gekrümmte Fläche paralell zu x,y-Ebene, geschnitten, hier in Höhe des Niveau z=0 (x,y-Ebene). Die Schnittmenge ist dann eine gekrümmte Linie in der Ebene.
z.B. x²+y² -r²=0 ergibt eine Kreis-Linie um Null mit Rad(r)
z.B. x²+y =0 ergibt eine Parabel.
z.B. xy -1=0 ergibt eine Hyperbel.
Die lineare Abb. zwischen den Diff. der quadr.Form entartet hier, wegen z=0, zu dz=0 :
dz: DxG*dx + DyG*dy =0 , => -DxG*dx =DyG*dy
Für den Kreis ergibt dieser Ausdruck:
Kreis: -2x*dx = 2y*dy , => y'= -x/y
5.6 Grenzwert-Berechnungen:
Um beim Bild-Differential Δy den Zusammenhang zum Quell-Differential Δx,
über die Funktion f(), zum Ausdruck zu bringen, schreibt man für Δy auch:
Δy = f(x+Δx) -f(x)
Jetzt können wir die Grenzübergänge, Δx ->0, für die verschiedenen Funktions-Typen f(), siehe Abschnitt 5.2 Satz a) - e), unterschuchen:
a) y=f(x)=const. ,hier gib es keine Veränderung im Bild, d.h. die f-Differenz ist an jedem Punkte-Paar p1,p2: f(p1)-f(p2) = const. -const. =0
Also ist dy/dx =d(f(x+Δx) -f(x)) /Δx =0/Δx = 0
b) y=f(x) =a*x , f(x+Δx) -f(x) =a(x+Δx) -a*x = a*Δx
=> a*Δx/Δx = a
c) Mittelbare Funktion: x->y->z ;z=g(y) und y=f(x)
=> dz/dy =g' ,dy/dx=f' (dy=f'*dx in dz/dy einsetzen):
=> dz/(f'*dx))= g' => dz/dx =g'*f'
d) Umkehr-Funktion: y=f(x) , x=g(y) , ist g Umkehrfunktion, dann gilt:
f(g(y)) = g(f(x)) =1 ,daraus folg nach c):
df/dy =dy/dy = f'**g' =1 oder dy/dy =dy/dx *dx/dy =1
=> dy/dx =1 / (dx/dy) = Relation für inverse Funktionen
e) y=f(x)=xn , n ganze Zahl
d(f(x+Δx) -f(x)) = (x+Δx)n -xn
Auflösung nach Binomischer Formel:
10*xn +n*xn-1Δx1 +A*xn-2Δx2 + . . . -xn
Der 1. und letzte Summand hebt sich auf, daraus folgt:
n*x(n-1)Δx1 +A*x(n-2)Δx2 +B*x(n-3)Δx3 . . .
Bei Division durch Δx bleibt im 1.Summand nur noch: n*xn-1 stehen. Alle weiteren Summanden beinhalten noch den Faktor Δx, so daß beim Grenzübergang Δx->0 diese Null werden, also gilt für den Diff.Quotienten:
d(xn)/dx = n*xn-1 Qed.
d) y=f(x)=xp/q , p,q ganze Zahl
Das Problem wird über die mittelbare Funktion gelöst:
Wir stzen z=x1/q => x=zq = dx/dz =q*zq-1
=> dy/dx =d( (x1/q)p ) = d(zp)/dx
=> dy/dz =p*zp-1 und dz/dx = 1/q *(x1/q)-(q-1)
=> dy/dx =dy/dz *dz/dx = p*zp-1 *1/q *x-(q-1)/q ,
für z: x 1/q einsetzen
=> dy/dx = p/q * (x1/q)p-1 *x-q/q-1/q)
=> = p/q * (x(p/q -1/q)) *x-1 +1/q)
=> = p/q * ((p/q -1/q -1 +1/q) )
=> d(xp/q)/dx = p/q *xp/q-1) Qed.
e) y=f(x)=exp(x) = 1 +1/1!x +1/2!x² +1/3!x³ +....
Summand-weise differenzieren:
=> dy/dx = 0 +x +1/2!x² +1/3!x³ +....
Die exp()-Funktion reproduziert sich, d.h. :
d(exp(x))/dx =exp(x) oder exp() genügt der
Diff.-Gleichung: Df=f
Aus Abschnitt 3.7 e), Modell der reellen Zahlen, wissen wir ,daß die Umkehr-Funktion
zur Potenz-Funktion exp(x) die Logarithmus-Funktion ln(x) ist.
Es gilt nach d) für y=exp(x): dy/dx =y
=> d(ln)/dy *dy/dx =1
=> d(ln)/dy =1/y oder auch d(ln)/dx =1/x
für die inverse Funktion g: g(exp(x))=x also, g(x)=ln(x)
f) (y-f(x))=0 oder allg. g(x,y)=0 , implizite Form
Das komplette Differential zu g lautet:
Dxg()*dx +Dyg()*dy =0 nbsp; , oder explizit:
Dx(y-f(x)))*dx +Dy(y-f(x))*dy =0
Dx(y-f(x)))*dx = 0-Dxf(x) und Dy(y-f(x)))*dy = 1-0
=> -Dxf(x)*dx + 1*dy =0 => f'*dx =dy
oder in de allg. Form [g(x,y)=0] :
=> Dxg*dx +Dyg*dy =0 => Dyg*dy = -Dxg*dx
=> dy/dx = -Dxg/Dyg
Interpretation:
Ist der Nenner (Dyg)≠0 ,hat man eine Gleichung (Differential-Gleichung) zur Bestimmung der hier abhängigen Variablen y() als Funktion der hier freien Variablen x.
kann auch umgekehrt vorgenemmen werden!
g) (u*v)' ,g=u*v, u=u(x),v=v(x)
Das komplette Differential zu u und v lautet:
dg =d(u*v) =Dug*du +Dvg*dv , Dvg=u ,Dug=v
=> g' =d(u*v)/dx =v*u' +u*v' , Produkt-Regel
f) Mittelwert-Satz:
Nach Voraussetzung ist f' ebnenfalls im kompakten Intervall (A,B) stetig. Daraus folgt:
1. f' ist beschränkt abs(f')≤k
2. Es gibt in (A,B) ein x°, so dass f'(x°) =(f(B)-f(A)/(B-A) umgekehrt gilt auch:
Zu 2 Punkten A',B' im Innern von (A,B) gibt es einen weiteren Pkt.x° ,A'≤x°≤B, so daß gilt:
f'(x°) =(f(B')-f(A')/(B'-A')
3. Ist f' überall Null, dann ist f=const.
Weitere Differentiationsregeln siehe: "Bronstein /Semendjajew ,7.Auflage, Seite 440"
Δy = f(x+Δx) -f(x)
Jetzt können wir die Grenzübergänge, Δx ->0, für die verschiedenen Funktions-Typen f(), siehe Abschnitt 5.2 Satz a) - e), unterschuchen:
a) y=f(x)=const. ,hier gib es keine Veränderung im Bild, d.h. die f-Differenz ist an jedem Punkte-Paar p1,p2: f(p1)-f(p2) = const. -const. =0
Also ist dy/dx =d(f(x+Δx) -f(x)) /Δx =0/Δx = 0
b) y=f(x) =a*x , f(x+Δx) -f(x) =a(x+Δx) -a*x = a*Δx
=> a*Δx/Δx = a
c) Mittelbare Funktion: x->y->z ;z=g(y) und y=f(x)
=> dz/dy =g' ,dy/dx=f' (dy=f'*dx in dz/dy einsetzen):
=> dz/(f'*dx))= g' => dz/dx =g'*f'
d) Umkehr-Funktion: y=f(x) , x=g(y) , ist g Umkehrfunktion, dann gilt:
f(g(y)) = g(f(x)) =1 ,daraus folg nach c):
df/dy =dy/dy = f'**g' =1 oder dy/dy =dy/dx *dx/dy =1
=> dy/dx =1 / (dx/dy)
e) y=f(x)=xn , n ganze Zahl
d(f(x+Δx) -f(x)) = (x+Δx)n -xn
Auflösung nach Binomischer Formel:
10*xn +n*xn-1Δx1 +A*xn-2Δx2 + . . . -xn
Der 1. und letzte Summand hebt sich auf, daraus folgt:
n*x(n-1)Δx1 +A*x(n-2)Δx2 +B*x(n-3)Δx3 . . .
Bei Division durch Δx bleibt im 1.Summand nur noch: n*xn-1 stehen. Alle weiteren Summanden beinhalten noch den Faktor Δx, so daß beim Grenzübergang Δx->0 diese Null werden, also gilt für den Diff.Quotienten:
d(xn)/dx = n*xn-1 Qed.
d) y=f(x)=xp/q , p,q ganze Zahl
Das Problem wird über die mittelbare Funktion gelöst:
Wir stzen z=x1/q => x=zq = dx/dz =q*zq-1
=> dy/dx =d( (x1/q)p ) = d(zp)/dx
=> dy/dz =p*zp-1 und dz/dx = 1/q *(x1/q)-(q-1)
=> dy/dx =dy/dz *dz/dx = p*zp-1 *1/q *x-(q-1)/q ,
=> dy/dx = p/q * (x1/q)p-1 *x-q/q-1/q)
=> = p/q * (x(p/q -1/q)) *x-1 +1/q)
=> = p/q * ((p/q -1/q -1 +1/q) )
=> d(xp/q)/dx = p/q *xp/q-1) Qed.
e) y=f(x)=exp(x) = 1 +1/1!x +1/2!x² +1/3!x³ +....
Summand-weise differenzieren:
=> dy/dx = 0 +x +1/2!x² +1/3!x³ +....
Die exp()-Funktion reproduziert sich, d.h. :
d(exp(x))/dx =exp(x) oder exp() genügt der
Diff.-Gleichung: Df=f
Aus Abschnitt 3.7 e), Modell der reellen Zahlen, wissen wir ,daß die Umkehr-Funktion
zur Potenz-Funktion exp(x) die Logarithmus-Funktion ln(x) ist.
Es gilt nach d) für y=exp(x): dy/dx =y
=> d(ln)/dy *dy/dx =1
=> d(ln)/dy =1/y oder auch d(ln)/dx =1/x
für die inverse Funktion g: g(exp(x))=x also, g(x)=ln(x)
Bemerkung:
Die exp()-Funktion ist die einzige Funktion, die abgeleitet sich selbst reproduziert!
Die exp()-Funktion ist die einzige Funktion, die abgeleitet sich selbst reproduziert!
f) (y-f(x))=0 oder allg. g(x,y)=0
Das komplette Differential zu g lautet:
Dxg()*dx +Dyg()*dy =0 nbsp; , oder explizit:
Dx(y-f(x)))*dx +Dy(y-f(x))*dy =0
=> -Dxf(x)*dx + 1*dy =0 => f'*dx =dy
oder in de allg. Form [g(x,y)=0] :
=> Dxg*dx +Dyg*dy =0 => Dyg*dy = -Dxg*dx
=> dy/dx = -Dxg/Dyg
Interpretation:
Ist der Nenner (Dyg)≠0 ,hat man eine Gleichung (Differential-Gleichung) zur Bestimmung der hier abhängigen Variablen y() als Funktion der hier freien Variablen x.
g) (u*v)' ,g=u*v, u=u(x),v=v(x)
Das komplette Differential zu u und v lautet:
dg =d(u*v) =Dug*du +Dvg*dv , Dvg=u ,Dug=v
=> g' =d(u*v)/dx =v*u' +u*v'
f) Mittelwert-Satz:
Nach Voraussetzung ist f' ebnenfalls im kompakten Intervall (A,B) stetig. Daraus folgt:
1. f' ist beschränkt abs(f')≤k
2. Es gibt in (A,B) ein x°, so dass f'(x°) =(f(B)-f(A)/(B-A) umgekehrt gilt auch:
Zu 2 Punkten A',B' im Innern von (A,B) gibt es einen weiteren Pkt.x° ,A'≤x°≤B, so daß gilt:
f'(x°) =(f(B')-f(A')/(B'-A')
3. Ist f' überall Null, dann ist f=const.
Weitere Differentiationsregeln siehe: "Bronstein /Semendjajew ,7.Auflage, Seite 440"
5.7 Beispiele:
Beispiel-1: f=(x-g(x))=0 , y=g(x)=x²
Dxf =1-0 , Dgf =0-1, Dxg =2x
=> Dxf*dx +Dgf *(Dxg *dx) =0 , Gleichung durch dy teilen:
=> 1*dx/dy -2x*dx/dy=0
=> 2x*dx/dy =1 => (2*x)dx =dy
Interpretation:
Dies ist eine gewöhnliche DGl. zur Bestimmung von y=g() als Funktion von x:
=> x² =y ,(Das war jetzt nur ein formales Beispiel, da die Funktion g() ja schon vorher bekannt war.)
Beispiel-2: f=(xy-1))=0 , y=g(x) gesucht:
Dxf =y , Dyf =x
=> y*dx +x*dy =0 => x*dy = -y*dx => dy/dx = -y/x
Variablen-Namen y durch die gesuchte Funktion g ersetzen:
=> g'=dg/dx =-g/x, =DGl. ,Lösung durch Trennung der Variablen:
=> 1/g *dg = -1/x *dx
=> ln(g) = -ln(x)
=> exp(ln(g)) = exp(-ln(x)) = [exp(ln(x))]-1
=> exp(ln(g)) = 1/x => g = 1/x
Probe: x*(1/x) -1 =0 Qed.
Dxf =1-0 , Dgf =0-1, Dxg =2x
=> Dxf*dx +Dgf *(Dxg *dx) =0
=> 1*dx/dy -2x*dx/dy=0
=> 2x*dx/dy =1 => (2*x)dx =dy
Interpretation:
Dies ist eine gewöhnliche DGl. zur Bestimmung von y=g() als Funktion von x:
=> x² =y ,(Das war jetzt nur ein formales Beispiel, da die Funktion g() ja schon vorher bekannt war.)
Beispiel-2: f=(xy-1))=0 , y=g(x) gesucht:
Dxf =y , Dyf =x
=> y*dx +x*dy =0 => x*dy = -y*dx => dy/dx = -y/x
Variablen-Namen y durch die gesuchte Funktion g ersetzen:
=> g'=dg/dx =-g/x
=> 1/g *dg = -1/x *dx
=> ln(g) = -ln(x)
=> exp(ln(g)) = exp(-ln(x)) = [exp(ln(x))]-1
=> exp(ln(g)) = 1/x => g = 1/x
Probe: x*(1/x) -1 =0 Qed.
5.8 Differential-Operator und Umkehrung:
Wir betrachten wieder allg. stetige Funktionen und differenzierbare Funktionen, siehe
Abschnitt 5.4 zuvor, im kompaktem Intervall M=(A,B).
Bei der Bildung des Differential-Quotienten an jedem Pkt. p in M wird als Grenzwert , soweit er existiert, eine reelle Zahl ermittelt.
Satz1:
Existiert der Differential-Quotient in einem Pkt.p, dann existiert er auch in einer ganzen δ-Umgebung von p.
Beweis: die Differentiale sind durch die sie verbindende Funktion f() , nach Def. und Voraussetzung, über das ε/δ(ε)-Kriterium, Abschnitt 5.4, verbunden:
d(Δxm- Δxn)<ε daraus folgt d(Δym- Δyn)<δ(ε) ,m>n
Gegeben sei eine Teil-Folge {m(i)}⊂{n}. Wir setzen Δym=B und Δyn=A . Wegen d(B-A))<δ(ε) gilt auch:
(Δym1-A) +(Δym2-Δym1)
+ ... +
+(Δym(k)-Δy(k-1)) +(B-Δyk)
=(B-A) <δ(ε) , die Δym(i) sind in
aufeinander-folgenden Summanden einmal "+" und einmal "-" ,
d.h., die Δym(k) bilden jeweils kleinere δ-Umgebungen im M und die Grenzwerte der Quell- und Bild-Differentiale existieren auch hier. Ende des Beweises
Folgerung1: Alle Quell-Differentiale werde in Bild-Differentiale abgebildet, so daß die Grenzwerte der Quotienten existieren und selbst eine reelle Variable bilden, nämlich y' =f'(x) die Ableitung von f() in M.
Folgerung2: Ist die Ableitung f' in einer ganzen δ-Umgebung const., speziell =0, dann ist sie auch im gesamten Def.Gebiet const.(=0).
Wichtiger ist der Umkehrschluß:
Satz2: Ist die Ableitungs-Funktion f' nicht const., dann nimmt f' einen bestimmten Wert, insbesondere Null, nur in einem isolierten Pkt. an, d.h. z.B., in die Differenz zur nächsten Nullstelle paßt eine ganze δ-Umgebung>0 hinein.
Folgerung3: Existiert die Ableitung f' zu einer Funktion f in M, dann kann der Differenzierungs-Prozeß als Abbildung von Funktionen zu Funktionen in M betrachtet werden, unter der Einschränkung, daß nicht alle stetigen Funktionen diff. in M sein müssen. (Beispiel: diskrete Funktion, die durch Verbinden zu stetiger Funktion gemacht wird)
Definition Operator(): Abbildungen in die Menge der reellen Zahlen heißen "Funktion()" , Abbildungen zu Funktionen heißen "Operator()" .
Der zuvor beschriebene Diff.-Prozeß ist demzufolge ein Operator, nämlich ein sogenannter "Differential-Operator()" . Symb.: Dx() oder f', wenn f() nur als Funktion einer einzigen Varaiablen betrachtet wird.
In diesem Fall werden andere Variable in f() als vorübergehend feste reelle-Zahlen (=Parameter) betrachtet. Ansonsten verwendet man symb. den "part.Diff-Operator" Dx(), um den Diff.-Prozeß in eine best. Richtung auszudrücken.
Definition Integral(): Wie bei allen Verknüpfungen zwischen Elementen im Euklid.Raum, ist auch hier, bei Abbildungen zwischen Funktionen, die Frage interessant:
Gibt es zum Diff.-Operator D() einen Umkehr-Operator, der die Funktion f'() wieder rückgängig macht, also die Ursprungs-Funktion f() vor Ableitung wiederherstellt?
1. Die Rückwärts-Richtung ist klar:
aus f'=D(f) folgt D-1(f')= D-1((D(f))=f
2. Def.: Die Umkehrung D-1() heißt:
Integral-Operator, symb.: I()
Die Existenz des I()-Operators für f'()-Funktionen ist gegeben, aber wie steht es mit Funktionen, die nicht aus einem Diff.-Prozeß entstanden sind?
Es muß also noch folgende Frage gelöst werden: Kann man zu einer gegebene Funktionen f() eine andere Funktion ermitteln, die wiederum abgeleitet, die geg. Funktion f() ergibt?
Da jede abgeleitete Funktion und auch jede sonst. Funktion auf M, (nach Voraussetzung), stetig ist, reduziert sich die Frage auf: Wie wird der Integrations-Prozeß I() für stet. Funktionen vorgenommen und wie kann man nachweisen, dass er duch einen Diff.-Prozeß wieder rückgängig gemacht werden kann?
Bei der Bildung des Differential-Quotienten an jedem Pkt. p in M wird als Grenzwert , soweit er existiert, eine reelle Zahl ermittelt.
Satz1:
Existiert der Differential-Quotient in einem Pkt.p, dann existiert er auch in einer ganzen δ-Umgebung von p.
Beweis: die Differentiale sind durch die sie verbindende Funktion f() , nach Def. und Voraussetzung, über das ε/δ(ε)-Kriterium, Abschnitt 5.4, verbunden:
d(Δxm- Δxn)<ε daraus folgt d(Δym- Δyn)<δ(ε) ,m>n
Gegeben sei eine Teil-Folge {m(i)}⊂{n}. Wir setzen Δym=B und Δyn=A . Wegen d(B-A))<δ(ε) gilt auch:
(Δym1-A) +(Δym2-Δym1)
+ ... +
+(Δym(k)-Δy(k-1)) +(B-Δyk)
=(B-A) <δ(ε)
d.h., die Δym(k) bilden jeweils kleinere δ-Umgebungen im M und die Grenzwerte der Quell- und Bild-Differentiale existieren auch hier.
Folgerung1: Alle Quell-Differentiale werde in Bild-Differentiale abgebildet, so daß die Grenzwerte der Quotienten existieren und selbst eine reelle Variable bilden, nämlich y' =f'(x) die Ableitung von f() in M.
Folgerung2: Ist die Ableitung f' in einer ganzen δ-Umgebung const., speziell =0, dann ist sie auch im gesamten Def.Gebiet const.(=0).
Wichtiger ist der Umkehrschluß:
Satz2: Ist die Ableitungs-Funktion f' nicht const., dann nimmt f' einen bestimmten Wert, insbesondere Null, nur in einem isolierten Pkt. an, d.h. z.B., in die Differenz zur nächsten Nullstelle paßt eine ganze δ-Umgebung>0 hinein.
Bemerkung:
Dieser Satz hat zentrale Bedeutung für die gesamte Analysis. Er ermöglicht es erst, Extremwert-Probleme oder auch Funktions-Gleichungen (Auflösungs-Theorie) zu lösen.
Dieser Satz hat zentrale Bedeutung für die gesamte Analysis. Er ermöglicht es erst, Extremwert-Probleme oder auch Funktions-Gleichungen (Auflösungs-Theorie) zu lösen.
Folgerung3: Existiert die Ableitung f' zu einer Funktion f in M, dann kann der Differenzierungs-Prozeß als Abbildung von Funktionen zu Funktionen in M betrachtet werden, unter der Einschränkung, daß nicht alle stetigen Funktionen diff. in M sein müssen. (Beispiel: diskrete Funktion, die durch Verbinden zu stetiger Funktion gemacht wird)
Definition Operator(): Abbildungen in die Menge der reellen Zahlen heißen "Funktion()" , Abbildungen zu Funktionen heißen "Operator()" .
Der zuvor beschriebene Diff.-Prozeß ist demzufolge ein Operator, nämlich ein sogenannter "Differential-Operator()" . Symb.: Dx() oder f', wenn f() nur als Funktion einer einzigen Varaiablen betrachtet wird.
In diesem Fall werden andere Variable in f() als vorübergehend feste reelle-Zahlen (=Parameter) betrachtet. Ansonsten verwendet man symb. den "part.Diff-Operator" Dx(), um den Diff.-Prozeß in eine best. Richtung auszudrücken.
Definition Integral(): Wie bei allen Verknüpfungen zwischen Elementen im Euklid.Raum, ist auch hier, bei Abbildungen zwischen Funktionen, die Frage interessant:
Gibt es zum Diff.-Operator D() einen Umkehr-Operator, der die Funktion f'() wieder rückgängig macht, also die Ursprungs-Funktion f() vor Ableitung wiederherstellt?
1. Die Rückwärts-Richtung ist klar:
2. Def.: Die Umkehrung D-1() heißt:
Integral-Operator, symb.: I()
Die Existenz des I()-Operators für f'()-Funktionen ist gegeben, aber wie steht es mit Funktionen, die nicht aus einem Diff.-Prozeß entstanden sind?
Es muß also noch folgende Frage gelöst werden: Kann man zu einer gegebene Funktionen f() eine andere Funktion ermitteln, die wiederum abgeleitet, die geg. Funktion f() ergibt?
Da jede abgeleitete Funktion und auch jede sonst. Funktion auf M, (nach Voraussetzung), stetig ist, reduziert sich die Frage auf: Wie wird der Integrations-Prozeß I() für stet. Funktionen vorgenommen und wie kann man nachweisen, dass er duch einen Diff.-Prozeß wieder rückgängig gemacht werden kann?
Bemerkung:
Diese Wechselwirkung zwischen Differential-Operator D() und Integral-Operator I() wird durch den sogenannten "Hauptsatz der Diff.- und Integral-Rechnung" zum Ausdruck gebracht.
Diese Wechselwirkung zwischen Differential-Operator D() und Integral-Operator I() wird durch den sogenannten "Hauptsatz der Diff.- und Integral-Rechnung" zum Ausdruck gebracht.
5.9 Integrations-Prozeß I():
Funktion f() ist vorgegeben, gesucht wird Funktion g() , so daß gilt: g'=f .
Beim Diff.-Operator handelt es sich um eine Quotienten-Bildung nach einer zuvor erfolgten Differenz-Bildung. Beides sind Verknüpfungen zwischen Elementen des Euklid.Raumes und werden durch die entspr. inversen Operationen Summen- bzw. Produkt-Bildung zurückgenommen, so daß man danach die Funktion g "freigelegt" hat.
1. Teilung einer Richtung zwischen 2 Punkten A,B:
Bild , Anal2-geo9.jpg
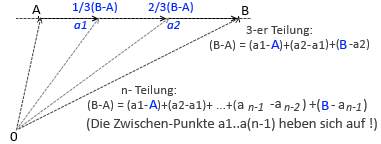
nach n-Halbierungen werden a(2n-1) Zwischen-Punkte gebildet mit den Differenzen benachbarter Punkte s(k)= a(k) -a(k-1):
s1: ( 1*2-n -A)
. . . . .
sk: ( k *2-n -(k-1)*2-n )
. . . . .
s(n-1): ( B -(n-1)*2-n)
Es gilt: s1 +s2 + . . .+s(j) =(B-A), für j -> ...2n
2. Setzt man a0=A und a(2n)=B , so existiert zu jedem a(i) , i=0...2n, der entspr. Funktionswert: g(a(i)) =g(i)
Jetzt können Quell- Differentiale Δx(i) und Bild- Differentiale g(i) gebildet werden:
Δx(i) =s(i) ,abs(s(i))= 1/2n
Δg(i) =g(i+1)-g(i) , i = 0...2n
3. Multipliziert man jedes g(i) mit dem entspr. s(i) und addiert alle Summanden auf, also: ..+g(i)*s(i)+... , so ergibt sich laut Konstruktion, (die Zwischen-Werte heben sich auf), als Ergebnis die Differenz g(B) -g(A)!
Da dies offensichtlich auch für beliebig große n gilt, kann man den Grenzübergang n->unendlich vornehmen:
Lim[n→∞](..+g(n)*s(n)+...) = g(B)-g(A)
4. Zur jeden Diff. Δg(i) =g(i+1)-g(i) gibt es laut Mittelwertsatz, siehe Abschnitt 5.6 Absatz f), einen Zwischenwert x° im zugehörigen Quell-Intervall s(i), so daß gilt:
Δg(i)/Δx(i) =g'(x°)
Satz:
2 benachbarte x° haben beim Grenzübergang n->∞ (= s(i)->0) einen beliebig kleinen Abstand.
Beweis: d(x°k - x°k-1) ≤ d(sk) +d(sk-1)
sk = k*2-n - (k-1)*2-n
sk-1 = (k-1)*2-n - (k-2)*2-n
d(sk) +d(sk-1) = k*2-n - (k-2)*2-n
= (k-k+2)*2-n =2*2-n
ε>0 vorgegeben, dann setzen wir n so groß, daß 2*2-n <ε ist.
=> d(x°k - x°k-1) ≤ d(sk) +d(sk-1) <ε
Ende des Beweises
Folgerung1:
Im >Lim[n→∞](..+g(n)*s(n)+...) kann man g(n) durch g(x°) und die s(n) durch Δx(n)->dx ersetzen, abs(dx)=Lim(1/2n).
Das Summ-Zeichen wird durch Integral-Zeichen "∫" mit Angabe der entsprechenden unteren und oberen Grenze A->B. Symb.: ∫[A,B](g(x°)*dx) , x°=reelle Variable zwischen A u.B
Def.: Diese Form wird bestimmtes Integral zu einer Funktion g() in den Grenzen von A->B genannt.
Folgerung2:
Da der Grenzwert, =reelle Zahl, der Ober-/Untersumme, (siehe folg. Beispiel 5.10), stetig von der oberen Grenze, also von der rechten Grenze im Quell-Intervall [x], abhängt, kann man die Flächen-Summe selbst als Funktion der variablen rechten Grenze [x] im Quell-Raum ansehen und somit als Bild-Funktion des Summen-(Integrations)-Prozesses betrachten. Diese (weitere) Bild-Funktion wird Stammfunktion F(x) zur sie erzeugenden Bild-Funktion f(x) genannt. (oder auch unbestimmtes Integral).
Wichtig: Der Integrations-Prozess (mit variabl.Obergrenze) ist gleichzusetzen mit dem Integral-Operator, weil er eine Abbildung einer Funktion in eine andere Funktion im gleichen Quell-Intervall darstellt. (Die Umkehrung wird dann durch den Differential-Operator bewerktstelligt)
Haupteigenschaft von F(x) ist: DF(x)=f(x). Durch diesen Zusammenhang gibt es umgekehrt zu jeder Funktion f unendl.viele Stammfunktionen, die sich nur in einer add.reellen Konstante unterscheiden. D(F(x)+c) =f(x).
Auf die Gleichheits-Beziehung zwischen zwei Funktionen F,f: D(F+c)=f kann also sofort der Integral-Operator ("∫") angewandt werden (df,dF Differentiale =Lim(Δ(F)),Lim(Δ(x) ) der Quell-,Bild-Menge):
∫(D(F(x)*dF)) =∫(f(x)*dx)
=> F(x)+c =∫(f(x)*dx)
Folgerung3:
Da die Differentiale dF und dx über: dF=f'dx im ganzen Intervall in Beziehung stehen, kann man auch die umgekehrte Frage stellen: Die Differentiale df,dx einer Bildfunktion f stehen immer in einer bestimmten Relation zueinander: df= c*dx, c=reelle Zahl. c kann im ganzen Intervall konstant sein, oder aber in jedem Pkt. verschieden, dann ist c eine reelle Funktion von [x], c=c(x). Nun könnte man folg. Frage stellen: Welche Funktion f paßt zu einer gegebenen Funktion c() in der Beziehung: df= c*dx. Die Lösung dieser Frage heißt:
Lösen einer DGL der Form: df= c()*dx
Folgerung4: (Aussagen zu stetigen Funktionen im kompakten Intervall):
Zu jeder stetigen Funktion gibt es eine Stammfunktion.
Jede Stammfunktion läßt sich differenzieren.
Umfangreiche Beziehungen zwischen F() und f() finden sich im: Bronstein/Semendjajew 7.Auflage 2008, 21.7 Tabellen, S.1074ff.
Beim Diff.-Operator handelt es sich um eine Quotienten-Bildung nach einer zuvor erfolgten Differenz-Bildung. Beides sind Verknüpfungen zwischen Elementen des Euklid.Raumes und werden durch die entspr. inversen Operationen Summen- bzw. Produkt-Bildung zurückgenommen, so daß man danach die Funktion g "freigelegt" hat.
1. Teilung einer Richtung zwischen 2 Punkten A,B:

nach n-Halbierungen werden a(2n-1) Zwischen-Punkte gebildet mit den Differenzen benachbarter Punkte s(k)= a(k) -a(k-1):
s1: ( 1*2-n -A)
. . . . .
sk: ( k *2-n -(k-1)*2-n )
. . . . .
s(n-1): ( B -(n-1)*2-n)
Es gilt: s1 +s2 + . . .+s(j) =(B-A)
2. Setzt man a0=A und a(2n)=B , so existiert zu jedem a(i) , i=0...2n, der entspr. Funktionswert: g(a(i)) =g(i)
Jetzt können Quell- Differentiale Δx(i) und Bild- Differentiale g(i) gebildet werden:
Δx(i) =s(i) ,abs(s(i))= 1/2n
Δg(i) =g(i+1)-g(i)
3. Multipliziert man jedes g(i) mit dem entspr. s(i) und addiert alle Summanden auf, also: ..+g(i)*s(i)+... , so ergibt sich laut Konstruktion, (die Zwischen-Werte heben sich auf), als Ergebnis die Differenz g(B) -g(A)!
Da dies offensichtlich auch für beliebig große n gilt, kann man den Grenzübergang n->unendlich vornehmen:
Lim[n→∞](..+g(n)*s(n)+...) = g(B)-g(A)
4. Zur jeden Diff. Δg(i) =g(i+1)-g(i) gibt es laut Mittelwertsatz, siehe Abschnitt 5.6 Absatz f), einen Zwischenwert x° im zugehörigen Quell-Intervall s(i), so daß gilt:
Satz:
2 benachbarte x° haben beim Grenzübergang n->∞ (= s(i)->0) einen beliebig kleinen Abstand.
Beweis: d(x°k - x°k-1) ≤ d(sk) +d(sk-1)
sk = k*2-n - (k-1)*2-n
sk-1 = (k-1)*2-n - (k-2)*2-n
d(sk) +d(sk-1) = k*2-n - (k-2)*2-n
= (k-k+2)*2-n =2*2-n
ε>0 vorgegeben, dann setzen wir n so groß, daß 2*2-n <ε ist.
=> d(x°k - x°k-1) ≤ d(sk) +d(sk-1) <ε
Folgerung1:
Im >Lim[n→∞](..+g(n)*s(n)+...) kann man g(n) durch g(x°) und die s(n) durch Δx(n)->dx ersetzen, abs(dx)=Lim(1/2n).
Das Summ-Zeichen wird durch Integral-Zeichen "∫" mit Angabe der entsprechenden unteren und oberen Grenze A->B. Symb.: ∫[A,B](g(x°)*dx) , x°=reelle Variable zwischen A u.B
Def.: Diese Form wird bestimmtes Integral zu einer Funktion g() in den Grenzen von A->B genannt.
Folgerung2:
Da der Grenzwert, =reelle Zahl, der Ober-/Untersumme, (siehe folg. Beispiel 5.10), stetig von der oberen Grenze, also von der rechten Grenze im Quell-Intervall [x], abhängt, kann man die Flächen-Summe selbst als Funktion der variablen rechten Grenze [x] im Quell-Raum ansehen und somit als Bild-Funktion des Summen-(Integrations)-Prozesses betrachten. Diese (weitere) Bild-Funktion wird Stammfunktion F(x) zur sie erzeugenden Bild-Funktion f(x) genannt. (oder auch unbestimmtes Integral).
Wichtig: Der Integrations-Prozess (mit variabl.Obergrenze) ist gleichzusetzen mit dem Integral-Operator, weil er eine Abbildung einer Funktion in eine andere Funktion im gleichen Quell-Intervall darstellt. (Die Umkehrung wird dann durch den Differential-Operator bewerktstelligt)
Haupteigenschaft von F(x) ist: DF(x)=f(x). Durch diesen Zusammenhang gibt es umgekehrt zu jeder Funktion f unendl.viele Stammfunktionen, die sich nur in einer add.reellen Konstante unterscheiden. D(F(x)+c) =f(x).
Auf die Gleichheits-Beziehung zwischen zwei Funktionen F,f: D(F+c)=f kann also sofort der Integral-Operator ("∫") angewandt werden (df,dF Differentiale =Lim(Δ(F)),Lim(Δ(x) ) der Quell-,Bild-Menge):
=> F(x)+c =∫(f(x)*dx)
Folgerung3:
Da die Differentiale dF und dx über: dF=f'dx im ganzen Intervall in Beziehung stehen, kann man auch die umgekehrte Frage stellen: Die Differentiale df,dx einer Bildfunktion f stehen immer in einer bestimmten Relation zueinander: df= c*dx, c=reelle Zahl. c kann im ganzen Intervall konstant sein, oder aber in jedem Pkt. verschieden, dann ist c eine reelle Funktion von [x], c=c(x). Nun könnte man folg. Frage stellen: Welche Funktion f paßt zu einer gegebenen Funktion c() in der Beziehung: df= c*dx. Die Lösung dieser Frage heißt:
Lösen einer DGL der Form: df= c()*dx
Folgerung4: (Aussagen zu stetigen Funktionen im kompakten Intervall):
Zu jeder stetigen Funktion gibt es eine Stammfunktion.
Jede Stammfunktion läßt sich differenzieren.
Umfangreiche Beziehungen zwischen F() und f() finden sich im: Bronstein/Semendjajew 7.Auflage 2008, 21.7 Tabellen, S.1074ff.
Beispiel zur Integral-Def. "Bestimmtes Integral 0->1":
5.10
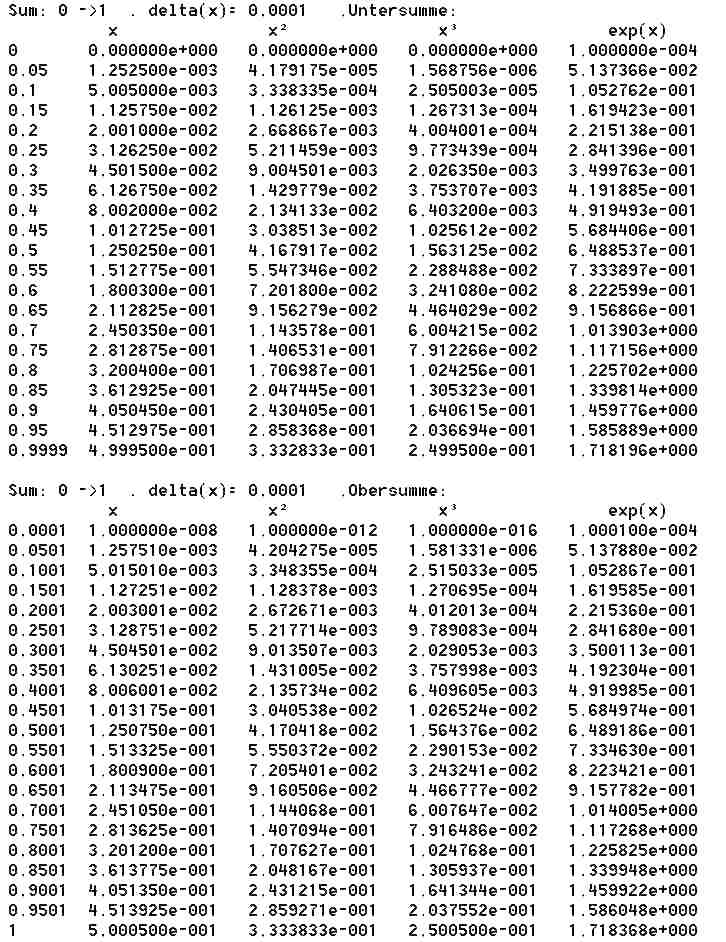
Bestimmtes Integral als Grenzwert von Summen von Rechteck-Flächen (Funktionswert*Delta(x)).
Nachfolgend ein Listing für Ober- und Untersummen-Berechnung zu Standard-Funktionen:
x, x², x³, exp(x):
Bild , Anal2-geo10.jpg
Algorithmus zu vorigem Listing:
Bild , Anal2-geo11.jpg


Algorithmus zu vorigem Listing:

5.11 Approximation von stetigen Funktionen:
M ist kompaktes Intervall und M°={f} Menge aller stetigen Funktionen in M
, also f∈M°.
1. Polynome:
[(x+(1-x)]n = ....+ (Bvn)*xv(1-x)n-v +... , 0≤v≤n , n=fest
Ist ein Polynom n-ten Grades, welches die Funktion f(x)=1 darstellt.
Wir betrachten f im Intervall 0-1 in (n+1)-Stützstellen {v/n}, v=0...n,
Dann ist das Polynom: P(f(v/n),n)= a0 +a1 +...a(n) ,
mit a(i)= f(i/n)*(Bin)*xi(1-x)n-i ,
eine differenzierbare Funktion zu f, die zu f einen Abstand hat von:
abs(f-P(f(v/n),n)) <ε =K/2*n*δ²
K ist abs(f)≤K (f ist beschränkt),
ε =Soll-Abstand in f,
δ =Abstand in 0-1, ≤abs(v/n -x)
Beispiel1: Wie hoch muß n gewählt werden, bei einem ε=0.2 und δ=0.1. Erg.: n >K/(0.2*0.1²) = K*500.
Beispiel2:Hat man ein abweichendes Intervall: x zwischen A,B , dann kann durch Variablen-Transformation x'= (x-A)/(B-A) das Standard-Intervall 0-1 wieder hergestellt werden.
Beispiel: Näherungs-Polynom 10-ten Grades:
Bild , Polynom1.jpg
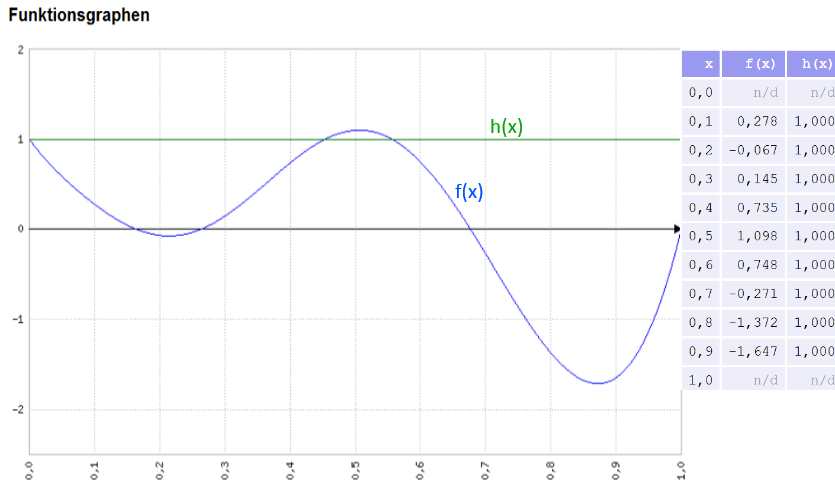
Polynom-Build zu f(x) Beispiel zuvor:
Bild , Polynom2.jpg

Nachfolgend ein Listing für die Berechnung von Binomial-Koeff. array={B(n)}:
Bild , Polynom3.jpg

Bild , Binom95_1.jpg

1. Polynome:
[(x+(1-x)]n = ....+ (Bvn)*xv(1-x)n-v +...
Ist ein Polynom n-ten Grades, welches die Funktion f(x)=1 darstellt.
Wir betrachten f im Intervall 0-1 in (n+1)-Stützstellen {v/n}, v=0...n,
Dann ist das Polynom: P(f(v/n),n)= a0 +a1 +...a(n) ,
mit a(i)= f(i/n)*(Bin)*xi(1-x)n-i ,
eine differenzierbare Funktion zu f, die zu f einen Abstand hat von:
abs(f-P(f(v/n),n)) <ε =K/2*n*δ²
K ist abs(f)≤K (f ist beschränkt),
ε =Soll-Abstand in f,
δ =Abstand in 0-1, ≤abs(v/n -x)
Beispiel1: Wie hoch muß n gewählt werden, bei einem ε=0.2 und δ=0.1. Erg.: n >K/(0.2*0.1²) = K*500.
Beispiel2:Hat man ein abweichendes Intervall: x zwischen A,B , dann kann durch Variablen-Transformation x'= (x-A)/(B-A) das Standard-Intervall 0-1 wieder hergestellt werden.
Bemerkung:
Man benötigt für hinrechende Genauigkeit enorme Potenzen für das Polynom P(). Zur Umwandlung von n-diskreten Punkten (Meßreihe) in stetige Funktion ist das praktisch, also rechentechnisch, nicht machbar. Der größte berechenbare Binomial-Koeff. ist (B4795) und ist eine 29-stellige Ganzzahl, was die Grenze der heutigen Computer darstellt.
Es ist zumindest eine theoretische Aussage, dass jede Funktion durch Polynome beliebig genau approx. werden kann. (Approximationssatz v. Weierstraß)
Man benötigt für hinrechende Genauigkeit enorme Potenzen für das Polynom P(). Zur Umwandlung von n-diskreten Punkten (Meßreihe) in stetige Funktion ist das praktisch, also rechentechnisch, nicht machbar. Der größte berechenbare Binomial-Koeff. ist (B4795) und ist eine 29-stellige Ganzzahl, was die Grenze der heutigen Computer darstellt.
Es ist zumindest eine theoretische Aussage, dass jede Funktion durch Polynome beliebig genau approx. werden kann. (Approximationssatz v. Weierstraß)

Polynom-Build zu f(x) Beispiel zuvor:

Nachfolgend ein Listing für die Berechnung von Binomial-Koeff. array={B(n)}:


Weitere Betrachtungen:
Euklidische Geometrie ,
Modell der reellen Zahlen ,
analytische Geometrie I ,
analytische Geometrie II ,
Euklidischer Raum ,
Analysis 1, Abbildungen ,
kleinere Beispiele der Himmelsmechanik im Newton-Modell ,
Bewegungen im Newton-Raum ,