| 3. Modell der rellen Zahlen zurück ->2.Euklid.Geometrie |
Ausgangspunkt
Entgegen den konstruktiv-anschaulichen Methoden der Eukl. Geometrie
basiert die Theorie der Reellen Zahlen (Eukl. Räume) auf einer abstrakten Herangehensweise.
Sie stützt sich dabei auf das Kalkül (Def. /Sätze /Folgerungen) aufbauend auf
3 Voraussetzungen:
a) Abzählbare Mengen
b) Algorithmen-Kalkül
c) Prinzip der vollständigen Induktion
Wenn man hierbei noch die Natur-Prinzipien Newton's hinzunimmt, so kann man das mechan. Weltmodell (Newton) hervorragend mit dem Eukl.Raum verbinden. In überschaubaren Umgebungen lassen sich dann die natürlichen Wechselwirkungen Gravitation, Elekrodynamik, Bewegungen usw. hinreichend genau mathematisch beschreiben.
Kernaussage der Prinzipien ist, daß es einem abstrakten Raum gibt (nicht zu verwechseln mit den hier behandelten math. abstrakten Räumen), der keine Dimension, Ausdehnung oder Masse hat, und in dem die Zeit gleichmäßig ruht o. fließt. Jeder phys.Raum, Körper, Masse ist vollständig in diesem abstr.Raum enthalten. Die phys. Elemente /Objekte können schrittweise ausgedehnt, vergrößert, zusammen- gefügt werden, aber nicht bis ins Unendliche o. nach Null, auch für Zeiten und Geschwindigkeit. Daraus kann man schon das Prinzip einer universellen max.Geschw. ableiten, später im relativ. Weltmodell von Einstein als Lichtgeschw. bezeichnet.
Zur Verdeutlichung logischer Sachverhalte im Kalkül werden wir durchaus auf graf. anschauliche Darstellungen zurückgreifen.
Der Ausgangspunkt sind die abzählbaren Mengen mit den Beziehungen zu natürl.Zahlen N=1,2,3,...
a) Abzählbare Mengen
b) Algorithmen-Kalkül
c) Prinzip der vollständigen Induktion
Wenn man hierbei noch die Natur-Prinzipien Newton's hinzunimmt, so kann man das mechan. Weltmodell (Newton) hervorragend mit dem Eukl.Raum verbinden. In überschaubaren Umgebungen lassen sich dann die natürlichen Wechselwirkungen Gravitation, Elekrodynamik, Bewegungen usw. hinreichend genau mathematisch beschreiben.
Kernaussage der Prinzipien ist, daß es einem abstrakten Raum gibt (nicht zu verwechseln mit den hier behandelten math. abstrakten Räumen), der keine Dimension, Ausdehnung oder Masse hat, und in dem die Zeit gleichmäßig ruht o. fließt. Jeder phys.Raum, Körper, Masse ist vollständig in diesem abstr.Raum enthalten. Die phys. Elemente /Objekte können schrittweise ausgedehnt, vergrößert, zusammen- gefügt werden, aber nicht bis ins Unendliche o. nach Null, auch für Zeiten und Geschwindigkeit. Daraus kann man schon das Prinzip einer universellen max.Geschw. ableiten, später im relativ. Weltmodell von Einstein als Lichtgeschw. bezeichnet.
Zur Verdeutlichung logischer Sachverhalte im Kalkül werden wir durchaus auf graf. anschauliche Darstellungen zurückgreifen.
Der Ausgangspunkt sind die abzählbaren Mengen mit den Beziehungen zu natürl.Zahlen
Diese Abhandlung besteht aus folgenden Abschnitten:
3.0
Abzählbare Mengen ( natürl.- ganze- rationale Zahlen )
->3.0
3.1.
Zusammenfassende Einleitung
->3.1
3.2.
Fundamentalfolgen ( Allg. Potenz-Reihe für rat.Zahl r )
->3.2
3.3.
Beispiele für konvergente Folgen
->3.3
3.4.
Sätze über konvergente Folgen
->3.4
3.5.
Rechnen mit reellen Zahlen
->3.5
3.6.
Eigenschaften der spez.Potenz-Reihe Pk(x) (Exponential-Funktion )
->3.6
3.7.
Mehrfach-Multiplikation von Zahlen (Potenz, -Umkehrfunktion )
->3.7
3.8.
Beispiel für Wachstums-Folge (all. Wachstumsprozeß Begriff )
->3.8
3.9.
n-dim abstrakter Eukl. Raum (Skapro, Abstands-Axiomatik u. Dreiecks-Ungleichung)
->3.9
3.10.
Fundamental-Folgen im Rm (δ-Umgebung, konvergente Folgen )
->3.10
3.11.
Punkt-Mengen im Rm (offene- /kompakte Umgebungen )
->3.11
3.12.
Zusammenfassung und Ausblick
->3.12
3.0 Abzählbare Mangen (G und R)
Abzählbare Mengen sind dadurch gekennzeichnet, dass man durch einen Auswahl-Algorithmus
die Elemente in eine Folge von indizierten Elementen überführen kann, so daß
bei einer Menge von n-Elementen folg. Folge ensteht: erstes Elem.,
zweites Elem., . . . , n-tes Elem.
Symb.: M = {E1, E2, ... ,En} oder, wenn die Element-Eigenschaft nicht mehr interessiert, sondern nur noch die Folge- Eigenschaft:
Symb.: M = {1, 2, ... ,n} Die "Folge" besitzt nur eine Eigenschaft, die Folge-Eigenschaft:
a) Es gibt nur ein erstes Element =1
b) Es gibt nur ein letztes Element =n
c) Alle übrigen Elemente k, 1 < k < n haben sowohl ein Vorgänger- als auch ein Nachfolge-Element.
Bemerkung: Eine Reihenfolge-Eigenschaft, also Relationen größer, kleiner, gleich kommt in M erst durch Hinzufügen einer Verknüpfung: Add/Sub zum Tragen.
Definition: Durch wiederholtes Anfügen eines weiteren Elementes o. Index, unter Anwend. des Prinzips der vollst.Induktion, erhält man eine unendliche o. abzählbar-unendliche Menge=Folge.
Symb.: M = {1, 2, ... ,n, ..} n=∞
Durch Hinzunahme eines entspr. neg. Index -k zu M und eines NULL-Elementes bekommt man bezügl. Add/Sub einen vollst. Raum.
Definition: G = {. . , -n, . . ,-1, 0, 1, . . ,n, . .} =Menge d. Ganzen Zahlen
1. sind a,b ∈G, dann ist c=a±b ebenfalls ∈G
2. sind a,b ∈G, dann ist die Gleichung a+x=b mit x ∈G immer lösbar:
x= 0, wenn a=b
x= b-a, a+b
3. a + b = b + a ,Kommutativ-Gesetz
4. a + b)+c = a +(b + c) ,Distributiv-Gesetz
Eine rationale Zahl r wird durch den Quotienten p/q , p,q∈G , definiert. Die Menge R ={p/q} , p,q ∈G , ist abzählbar, da man offensichtlich der Reihe nach auf jedes r ∈G zeigen kann.
In der Menge der rationalen Zahlen ist eine weitere Verknüpfung def., die Mult./Div.
Definition: R = {r1, r2, . . .} , ri=p/q , p,q ∈G , R=Menge rat.Zahlen:
1) Add/Sub wie bei G=ganze Zahlen
2) Die Mult./Div. zweier rat.Zahlen ist wieder rat.Zahl, wobei gilt:
a) r1 * r2 = r2 * r1
b) (r1*r2)* r3 = r1*(r2* r3)
c) r1 *1 = r1 , 1= neutrales Element
d) r1 *x = r2 , für r1 ≠0
x = r2 / r1 , für r1 ≠0
x = 1 , für r1=r2
e) (r1+ r2) *r3 = (r1*r3) + (r2*r3) , (Distributiv)
Durch die Verknüpfungen können in R Relationen definiert und Teilfolgen sortiert werden.
Definition von Relationen:
a) sign (Vorzeichen) einer rat.Zahl
sign(r) = {+1,r>0 , =0,r=0 , -1,r<0 }
b) abs(r) = r * sign(r) ,(Absolut-Betrag)
c) r1 - r2 >0 ==> r1 > r2
r1 - r2 =0 ==> r1 = r2
r1 - r2 r<0 ==> r1 r< r2
d) Folge F{r1, r2, . . ., rn }
Die größte der Zahlen in F heißt:
max(F), alternativ min(F)
e) Rechengesetze für Ungleichungen
r1<r2 und r2<r3 : r1<r3
r1<r2 : r1+r < r2+r
r1<r2 und r3<r4 : r1+r3 < r2+r4
r1<r2 und r>0 : r1*r < r2*r
0<r1<r2 , 0<r3<r4 : r1*r3 < r3*r4
0<r1<r2 : 1/r1 < 1/r2
Wichtiger Satz für Ungleichungen:
Satz1: (1+h)n ≥ 1+n*h , n∈N , h>-1
Beweis:
1. n=1: (1+h) ≥ 1+h , richtig
2. n: (1+h)n ≥ 1+n*h , sei richtig, dann soll auch
(1+h)n+1 ≥ 1+(n+1)*h , sein
(1+h)n*(1+h) ≥ (1+n*h)*(1+h) = 1 +nh +h +nh²
wegen nh²≥0 gilt: (1+h)n+1 ≥ 1+(n+1)*h
Qed
f) Rechengesetze für abs()
1. abs(r1 * r2) = abs(r1) * abs(r2)
Beweis durch Fallunterscheidung!
2. abs(r1 /r2) = abs(r1) / abs(r2) für r2≠0
3. abs(r1 +r2) ≤ abs(r1) +abs(r2) , Dreiecks-Ungl.
Beweis durch Fallunterscheidung!
3. abs(r1 +r2) ≤ abs(r1) +abs(r2) , Dreiecks-Ungl.
4. abs(r1 +r2) ≥ abs[ abs(r1) -abs(r2) ]
gegenteilige Dreiecks-Ungleichung
g) Abstands-Def. in R=rat.Zahlen
r1,r2∈R , dann wird der Ausdruck abs(r1-r2) als Abstand=d zwischen 2 Element-Zahlen von R bezueichnet.
Symb.: d(r1,r2) =d(r2,r1) = abs(r1,r2) =abs(r2,r1)
Eigenschaften:
1. Abstand d ist Zahl ≥0
2. Symmetrie , d(r1,r2) =d(r2,r1)
3. Gleichheit: d(r1,r2)=0 , ==> r1=r2
4. Dreiecks-Ungleichung: Der Umweg über weiteren Pkt. ist immer länger o. gleich dem direkten Weg.
Symb.: M = {E1, E2, ... ,En} oder, wenn die Element-Eigenschaft nicht mehr interessiert, sondern nur noch die Folge- Eigenschaft:
Symb.: M = {1, 2, ... ,n} Die "Folge" besitzt nur eine Eigenschaft, die Folge-Eigenschaft:
a) Es gibt nur ein erstes Element =1
b) Es gibt nur ein letztes Element =n
c) Alle übrigen Elemente k, 1 < k < n haben sowohl ein Vorgänger- als auch ein Nachfolge-Element.
Bemerkung: Eine Reihenfolge-Eigenschaft, also Relationen größer, kleiner, gleich kommt in M erst durch Hinzufügen einer Verknüpfung: Add/Sub zum Tragen.
Definition: Durch wiederholtes Anfügen eines weiteren Elementes o. Index, unter Anwend. des Prinzips der vollst.Induktion, erhält man eine unendliche o. abzählbar-unendliche Menge=Folge.
Symb.: M = {1, 2, ... ,n, ..} n=∞
Durch Hinzunahme eines entspr. neg. Index -k zu M und eines NULL-Elementes bekommt man bezügl. Add/Sub einen vollst. Raum.
Definition: G = {. . , -n, . . ,-1, 0, 1, . . ,n, . .} =Menge d. Ganzen Zahlen
1. sind a,b ∈G, dann ist c=a±b ebenfalls ∈G
2. sind a,b ∈G, dann ist die Gleichung a+x=b mit x ∈G immer lösbar:
x= 0, wenn a=b
x= b-a, a+b
3. a + b = b + a ,Kommutativ-Gesetz
4. a + b)+c = a +(b + c) ,Distributiv-Gesetz
Eine rationale Zahl r wird durch den Quotienten p/q , p,q∈G , definiert. Die Menge R ={p/q} , p,q ∈G , ist abzählbar, da man offensichtlich der Reihe nach auf jedes r ∈G zeigen kann.
In der Menge der rationalen Zahlen ist eine weitere Verknüpfung def., die Mult./Div.
Definition: R = {r1, r2, . . .} , ri=p/q , p,q ∈G , R=Menge rat.Zahlen:
1) Add/Sub wie bei G=ganze Zahlen
2) Die Mult./Div. zweier rat.Zahlen ist wieder rat.Zahl, wobei gilt:
a) r1 * r2 = r2 * r1
b) (r1*r2)* r3 = r1*(r2* r3)
c) r1 *1 = r1 , 1= neutrales Element
d) r1 *x = r2 , für r1 ≠0
x = r2 / r1 , für r1 ≠0
x = 1 , für r1=r2
e) (r1+ r2) *r3 = (r1*r3) + (r2*r3) , (Distributiv)
Durch die Verknüpfungen können in R Relationen definiert und Teilfolgen sortiert werden.
Definition von Relationen:
a) sign (Vorzeichen) einer rat.Zahl
sign(r) = {+1,r>0 , =0,r=0 , -1,r<0 }
b) abs(r) = r * sign(r) ,(Absolut-Betrag)
c) r1 - r2 >0 ==> r1 > r2
r1 - r2 =0 ==> r1 = r2
r1 - r2 r<0 ==> r1 r< r2
d) Folge F{r1, r2, . . ., rn }
Die größte der Zahlen in F heißt:
max(F), alternativ min(F)
e) Rechengesetze für Ungleichungen
r1<r2 und r2<r3 : r1<r3
r1<r2 : r1+r < r2+r
r1<r2 und r3<r4 : r1+r3 < r2+r4
r1<r2 und r>0 : r1*r < r2*r
0<r1<r2 , 0<r3<r4 : r1*r3 < r3*r4
0<r1<r2 : 1/r1 < 1/r2
Wichtiger Satz für Ungleichungen:
Satz1: (1+h)n ≥ 1+n*h , n∈N , h>-1
Beweis:
1. n=1: (1+h) ≥ 1+h , richtig
2. n: (1+h)n ≥ 1+n*h , sei richtig, dann soll auch
(1+h)n+1 ≥ 1+(n+1)*h , sein
(1+h)n*(1+h) ≥ (1+n*h)*(1+h) = 1 +nh +h +nh²
wegen nh²≥0 gilt: (1+h)n+1 ≥ 1+(n+1)*h
Qed
f) Rechengesetze für abs()
1. abs(r1 * r2) = abs(r1) * abs(r2)
Beweis durch Fallunterscheidung!
2. abs(r1 /r2) = abs(r1) / abs(r2) für r2≠0
3. abs(r1 +r2) ≤ abs(r1) +abs(r2) , Dreiecks-Ungl.
Beweis durch Fallunterscheidung!
3. abs(r1 +r2) ≤ abs(r1) +abs(r2) , Dreiecks-Ungl.
4. abs(r1 +r2) ≥ abs[ abs(r1) -abs(r2) ]
gegenteilige Dreiecks-Ungleichung
g) Abstands-Def. in R=rat.Zahlen
r1,r2∈R , dann wird der Ausdruck abs(r1-r2) als Abstand=d zwischen 2 Element-Zahlen von R bezueichnet.
Symb.: d(r1,r2) =d(r2,r1) = abs(r1,r2) =abs(r2,r1)
Eigenschaften:
1. Abstand d ist Zahl ≥0
2. Symmetrie , d(r1,r2) =d(r2,r1)
3. Gleichheit: d(r1,r2)=0 , ==> r1=r2
4. Dreiecks-Ungleichung: Der Umweg über weiteren Pkt. ist immer länger o. gleich dem direkten Weg.
3.1 Zusammenfassende Einleitung:
Wir haben bisher abzählbare Mengen zu Mengen von Inizes 1,...,n abstahiert
und die einfache Indexfolge in die Menge aller Index-Quotienten p/q , p,q∈N
umgeordnet. Dieser Menge habe wir die elementaren Rechen-Operationen Add/Mult.
zugefügt samt ihrer Umkehr-Operationen Sub/Div , so daß man beliebige Elemente
=Indizes mit diesen verknüpfen kann und das Ergebnis wiederum ∈R ist.
Dabei wurden Grenzübergänge n->∞ nur bezügl. Anz. der Elemente vorgenommen, nicht jedoch bezügl. Anz. nacheinander auszuführender Operationen.
In der folg. Entwicklung des Modells wird es darauf ankommen, abstakte Kalküls zu verwenden, also Grenzwerte-Bestimmung von Potenzreihen, wobei wir schon aus Abschnitt "1.13 Teilung der Eins-Strecke und Rationale Zahlen" wissen, dass die sogenannte Dez.Teilung: a= a1/10 +a2/10² +a2/10³ + . . . im Allgemeinen nicht zu einer rat.Zahl a=p/q führt.
Kernstück des Modells reell.Zahlen wird das Instrument der "Fundamental-Folge" sein, also Folgen von Elementen, die mittels des Abstands-Begriffes auf Konvergenz untersucht werden. Der Grenzwert ist dabei unabhängig von der konkreten Folge. Zum Beispiel hat F1={1/n} den gleichen Grenzwert=0, wie F2={1/n²}.
Die Grenwerte selbst sind dann Repräsentanten aller Fundamental-Folgen, die den gleichen Grenzwert haben. Da die Grenzwerte nicht nur rat.Zahlen sind, ist die Gesamtmenge aller Grenzwerte von Folgen mächtiger als die der abzähl. rat.Zahlen.
Diese neue, nicht mehr abzählbare, Menge nennt man die "Menge der Reellen Zahlen" , symb. R (rat.+ irrat. Zahlen).
Zum Schluß sei noch darauf hingewiesen, das jedes Element von R als Grenzwert von Fundamental-Folgen auch Häufungspunkt innerhalb R ist. Mit diesen Eigenschaften können dann auch die höheren Verknüpfungen Potenz und Umkehrung Wurzel/Log. beschrieben werden.
Dabei wurden Grenzübergänge n->∞ nur bezügl. Anz. der Elemente vorgenommen, nicht jedoch bezügl. Anz. nacheinander auszuführender Operationen.
In der folg. Entwicklung des Modells wird es darauf ankommen, abstakte Kalküls zu verwenden, also Grenzwerte-Bestimmung von Potenzreihen, wobei wir schon aus Abschnitt "1.13 Teilung der Eins-Strecke und Rationale Zahlen" wissen, dass die sogenannte Dez.Teilung: a= a1/10 +a2/10² +a2/10³ + . . . im Allgemeinen nicht zu einer rat.Zahl a=p/q führt.
Kernstück des Modells reell.Zahlen wird das Instrument der "Fundamental-Folge" sein, also Folgen von Elementen, die mittels des Abstands-Begriffes auf Konvergenz untersucht werden. Der Grenzwert ist dabei unabhängig von der konkreten Folge. Zum Beispiel hat F1={1/n} den gleichen Grenzwert=0, wie F2={1/n²}.
Die Grenwerte selbst sind dann Repräsentanten aller Fundamental-Folgen, die den gleichen Grenzwert haben. Da die Grenzwerte nicht nur rat.Zahlen sind, ist die Gesamtmenge aller Grenzwerte von Folgen mächtiger als die der abzähl. rat.Zahlen.
Diese neue, nicht mehr abzählbare, Menge nennt man die "Menge der Reellen Zahlen" , symb. R (rat.+ irrat. Zahlen).
Zum Schluß sei noch darauf hingewiesen, das jedes Element von R als Grenzwert von Fundamental-Folgen auch Häufungspunkt innerhalb R ist. Mit diesen Eigenschaften können dann auch die höheren Verknüpfungen Potenz und Umkehrung Wurzel/Log. beschrieben werden.
3.2 Fundamentalfolgen
Definition delta-Umgebung:
Die Menge aller r, die von r0 einen Abstand d(r0)<δ
haben, bilden die δ-Umgebung von r0.
Symb.: Uδ(r0)
Definition Folge: Ordnet man jeder natürlichen Zahl n eine rat.Zahl zu, entsteht eine unendl. abzählbare Folge:
r1 , r2 , . . . , rn , . . .
Symb.:F={rn} ,n=1,2,....
Definition Beschränkheit Folge: Eine Folge {rn} heißt beschränkt, wenn es zwei Zahlen a,b gibt, a<b, gibt, wobei für alle rn gilt: a ≤ rn ≤ b
Definition Konvergenz Folge: Eine Folge {rn} heißt konvergent, wenn es eine Zahl r gibt, mit der Eigenschaft, daß in jeder δ-Umgebung von r alle rn liegen, für hinreichend große n .
Anders formuliert: Es gibt einen Index n, so daß der Abstand zweier nachf. Elemente kleiner δ ist: d(rk,rm)<δ, k>n, m>n
Symb.: δ>0 ==> ∃Nδ: abs(rn -rm) <δ , ∀n,m>Nδ
Ist dieses δ-Konvergenz-Kriterium erfüllt, dann heißt r Limes, Grenzwert, Häufungspunkt der Folge {rn} , symb: rn->r oder lim(rn)=r
Null-Folge: Für {rn}->0 hat das δ-Konvergenz-Kriterium die spezielle Form:
δ>0 ==> ∃Nδ: abs(rn) <δ , ∀n≥Nδ
Beispiel für Folge:
Bewegung eines Masse-Punktes zwischen 2 Zeitpunkten t1 und t2.
Wir bilden A={rn} , rn =t2 -(t2 -t1)/n
1. r=t1 für n=1 (Anf.Zeitpunkt)
2. r=t2 für n=∞ (End.Zeitpkt.)
3. rn sind beschränkt: a=min(t1,t2) und b=max(t1,t2) ,Beweis:
1.Fall: a=t1 , b=t2 , (t2-t1)>0
=> t1 ≤ t2-(t2-t1)/n ≤ t2
=> t1-t1 ≤ (t2-t1)-(t2-t1)/n ≤ t2-t1
=> 0 ≤ 0 ≤ +(t2-t1)/n(wegen (t2-t1)>0)
=> n≤1 ,Qed. 1.Fall
2.Fall: a=t2 , b=t1 , (t1-t2)>0
=> t2 ≤ t2-(t2-t1)/n ≤ t1
=> t2-t2 ≤ 0 -(t2-t1)/n ≤ t1-t2
=> 0 ≤ +(t1-t2)/n ≤ t1-t2(wegen (t1-t2)>0)
=> n≤1 ,Qed. 2.Fall
4. δ-Konvergenz-Kriterium:
Ab welchem Index n und m>n ist die folg. Ungleichung richtig?
abs(rm-rn)<δ=p/q :
abs(t2 -(t2 -t1)/m -[t2 -(t2 -t1)/n]) <δ
=> abs(-(t2 -t1)/m +(t2 -t1)/n ) <p/q
=> abs(t2 -t1) * (1/n -1/m) <p/q
a=abs(t2 -t1) setzen :
=> (1/n -1/m) <p/(q*a) wegen m>n gilt:
=> (1/n -1/m) < 1/n <p/(q*a)
=> 1/n <p/(q*a) n=(q+1)*a setzen :
=> 1/[(q+1)*a] < p/(q*a) richtig für p≥1
Qed. δ-Konv.-Kriterium
5. Grenzwert: Mit dem δ-Konv.-Kriterium prüft man zunächst nur, ob Konvergenz vorliegt, den Grenzwert kann man damit nicht ermitteln. Eine Methode zur Grenzwert-Ermittlung wäre: Alle Element-Differenzen zum Vorgänger-Element aufadd. bis n=unendl. :
S(n)=... +(rn-rn-1) , n=1,2,...
==> S(n)= rn -r1
==> S(n)= (t2 -(t2 -t1)/n -(t2 -(t2 -t1)/1
==> S(∞)= t2 -0 -(t2 -(t2 -t1) = t2-t1
Da wir mit Zeitpkt.t1 begonn. hatten ist:
t1 +S(∞) =t1 +(t2-t1) =t2 =Lim(A)
Ende Beispiel für Folge
Symb.:
Definition Folge: Ordnet man jeder natürlichen Zahl n eine rat.Zahl zu, entsteht eine unendl. abzählbare Folge:
r1 , r2 , . . . , rn , . . .
Symb.:
Definition Beschränkheit Folge: Eine Folge {rn} heißt beschränkt, wenn es zwei Zahlen a,b gibt, a<b, gibt, wobei für alle rn gilt:
Definition Konvergenz Folge: Eine Folge {rn} heißt konvergent, wenn es eine Zahl r gibt, mit der Eigenschaft, daß in jeder δ-Umgebung von r alle rn liegen, für hinreichend große n .
Anders formuliert: Es gibt einen Index n, so daß der Abstand zweier nachf. Elemente kleiner δ ist: d(rk,rm)<δ, k>n, m>n
Symb.: δ>0 ==> ∃Nδ: abs(rn -rm) <δ , ∀n,m>Nδ
Ist dieses δ-Konvergenz-Kriterium erfüllt, dann heißt r Limes, Grenzwert, Häufungspunkt der Folge {rn} , symb: rn->r oder lim(rn)=r
Null-Folge: Für {rn}->0 hat das δ-Konvergenz-Kriterium die spezielle Form:
δ>0 ==> ∃Nδ: abs(rn) <δ , ∀n≥Nδ
Beispiel für Folge:
Bewegung eines Masse-Punktes zwischen 2 Zeitpunkten t1 und t2.
Wir bilden A={rn} , rn =t2 -(t2 -t1)/n
1. r=t1 für n=1 (Anf.Zeitpunkt)
2. r=t2 für n=∞ (End.Zeitpkt.)
3. rn sind beschränkt: a=min(t1,t2) und b=max(t1,t2) ,Beweis:
1.Fall: a=t1 , b=t2 , (t2-t1)>0
=> t1 ≤ t2-(t2-t1)/n ≤ t2
=> t1-t1 ≤ (t2-t1)-(t2-t1)/n ≤ t2-t1
=> 0 ≤ 0 ≤ +(t2-t1)/n
=> n≤1 ,Qed. 1.Fall
2.Fall: a=t2 , b=t1 , (t1-t2)>0
=> t2 ≤ t2-(t2-t1)/n ≤ t1
=> t2-t2 ≤ 0 -(t2-t1)/n ≤ t1-t2
=> 0 ≤ +(t1-t2)/n ≤ t1-t2
=> n≤1 ,Qed. 2.Fall
4. δ-Konvergenz-Kriterium:
Ab welchem Index n und m>n ist die folg. Ungleichung richtig?
abs(rm-rn)<δ=p/q :
abs(t2 -(t2 -t1)/m -[t2 -(t2 -t1)/n]) <δ
=> abs(-(t2 -t1)/m +(t2 -t1)/n ) <p/q
=> abs(t2 -t1) * (1/n -1/m) <p/q
a=abs(t2 -t1) setzen :
=> (1/n -1/m) <p/(q*a)
=> (1/n -1/m) < 1/n <p/(q*a)
=> 1/n <p/(q*a)
=> 1/[(q+1)*a] < p/(q*a)
Qed. δ-Konv.-Kriterium
5. Grenzwert: Mit dem δ-Konv.-Kriterium prüft man zunächst nur, ob Konvergenz vorliegt, den Grenzwert kann man damit nicht ermitteln. Eine Methode zur Grenzwert-Ermittlung wäre: Alle Element-Differenzen zum Vorgänger-Element aufadd. bis n=unendl. :
S(n)=... +(rn-rn-1) , n=1,2,...
==> S(n)= rn -r1
==> S(n)= (t2 -(t2 -t1)/n -(t2 -(t2 -t1)/1
==> S(∞)= t2 -0 -(t2 -(t2 -t1) = t2-t1
Da wir mit Zeitpkt.t1 begonn. hatten ist:
t1 +S(∞) =t1 +(t2-t1) =t2 =Lim(A)
3.3 Beispiele für konvergente Folgen:
a. konst.Folge Es seien alle rn=r, dann ist {rn}
konvergent mit: Lim(rn)=r
b. Null-Folge {1/rn} ist Null-Folge. Beweis:
abs(1/n -1/(n+m)) <δ =p/q ,
(1/n -1/(n+m)) = (n+m -n)/(n*(n+m))
==> m/(n*(n+m)) = 1/n * m/(n+m)
==> 1/n * m/(n+m) <1/n ,für n≥(q+1) gilt:
1/(q+1) < p/q =δ Qed. Null-Folge
c. Potenz-Folge {rn} ist Null-Folge für abs(r)<1 , Beweis:
1. Fall r=0, dann nach Beispiel a) Grenzwert=0
2. Fall 0<r<1 : setzen h=1/r -1 , d.h. h>0 und abs(r)=1/(1+h)
==> rn = 1/(1+h)n ≤ 1/(1+n*h) (wegen Ungleichung
Satz1 aus Abschnitt 3.0)
==> Bei δ=p/q wird n so gewählt, dass 1+n*h >q ist, dann gilt:
1/(1+n*h) < 1/q ≤ p/q , Qed 2.Fall
3. Fall -1<r<0 : setzen h=1/(-r) -1 , bei h>0 folgt: r= -1/(1+h), weil auch hier abs(r)=1/(1+h) ist, gilt das Gleiche wie unter 2.Fall. Qed 3.Fall
d. {rn} sei Folge mit:
r1=1 ,r2=1+r ,r3=1+r+r² ,...
rn=1+r+r²...+ rn-1
n-tes Glied abschätzen:
rn = 1 +r +r²...+rn-1
rn*r= r +r²...+rn-1 +rn
rn -rn*r = rn*(1-r) = 1+rn
=> rn= (1+rn)/(1-r)
Man sieht sofort, dass der Limes =1/(1-r) ist.
δ-Kriterium mit Limes abschätzen:
abs(rn - 1/(1-r) ) < p/q
abs((1+rn)/(1-r) - 1/(1-r) ) < p/q
Für abs(r) <1 gilt:
1/(1-r) *abs(rn) < p/q
Für abs(rn) hatten wir in c) Potenz-Folge ein δ
und Nδ gefunden. Wir bilden δ' =δ*(1-r) und
N'δ= Nδ*(1-r)
Mit δ' und N'δ ist die Konvergenz-Bedingung erfüllt.
Ende Beispiel d) Folge
e) Allg. Potenz-Reihe für rat.Zahl r
Wir bilden die Reihe rn aus d) neu:
Rn = r +r²... + rn
Rn*r= r²... + rn + rn+1
=> Rn -Rn*r = r + rn+1
=> Rn = (r + rn+1) /(1-r) r=1/b setzen :
=> Rn = (1 + 1/bn+1) / (b-1) Lim(rn)01/(b-1) :
=> R = a* [1/b +1/b² +1/b³ +...] =a/(b-1) ,a=1
Setzen wir a=p und b=q+1 so erhalten wir:
Satz1: über abzählbare Mengen
Alle rat. Zahlen p/q lassen sich als (unendl.) Potenzreihe der Form:
p/q =p* [1/(q+1) +1/(q+1)² +...] darstellen.
f) Dez.-Ziffern-Darstell. als Spez.Fall von rn
In rn = 1 +r +r²...+rn-1 r durch 1/p ersetzen:
rn = 1 +1/p +1/p²...+1/pn-1 Grenzwert nach d):
= p(1 +1/pn)/(p-1) Add -1 auf beiden Seiten:
rn = 1/p +1/p²...+1/pn-1 = (1 +1/pn)/(p-1)
Setzt man p=10, so bekommt man die bekannte Dez.Darstellung von rn= 1/9 auf n-1 Stellen nach Komma +(rat.)Restglied:
1/9 =1/10 +1/10²...+1/10n-1 +1/(9*10n)
bei n=∞: 1/9 =0,1111...1... (Zykl.)
Folgerung: Verallgemeinerung :
r =(p-1) *[1/p +1/p²...+1/p∞] =(p-1)/(p-1) =1
Wenn man q1,q2,q3..->∞ alle=1 setzt, folgt:
1 =(p-1) *[q1/p +q2/p²... ] ,für p>0
Sind nun alle Koeff. qn ,n=1,2,... verschieden (ohne Zyklus) ,so erhält man eine unendl. Potenz-Reihe aus rat. Elementen, wobei der Grenzwert keine rationale Zahl mehr ist!Sie dazu Abhandlung 1.13 und 1.14
Aussage 1:
Die Partialsummen der Reihen R in Satz 1 bilden eine konvergente Folge. Daraus kann man schlußfolgern: Alle rat. Zahlen sind Grenzwert und damit Häufungspunkt in der Menge M.
Aussage 2:
Die Grenzwerte von Potenzreihen mit rat. Elementen sind nur bei endl. vielen Gliedern (o. Zykl.) selbst wieder rat.Zahlen, ansonsten irrat. Zahlen.
Aussage 3:
Jede Dez.-Ziffern-Darstell. mit endlich vielen Stellen rechts vom Komma bezeichnet umkehrbar eindeutig eine rat.Zahl.
b. Null-Folge {1/rn} ist Null-Folge. Beweis:
abs(1/n -1/(n+m)) <δ =p/q ,
(1/n -1/(n+m)) = (n+m -n)/(n*(n+m))
==> m/(n*(n+m)) = 1/n * m/(n+m)
==> 1/n * m/(n+m) <1/n ,für n≥(q+1) gilt:
1/(q+1) < p/q =δ Qed. Null-Folge
c. Potenz-Folge {rn} ist Null-Folge für abs(r)<1 , Beweis:
1. Fall r=0, dann nach Beispiel a) Grenzwert=0
2. Fall 0<r<1 : setzen h=1/r -1 , d.h. h>0 und abs(r)=1/(1+h)
==> rn = 1/(1+h)n ≤ 1/(1+n*h)
==> Bei δ=p/q wird n so gewählt, dass 1+n*h >q ist, dann gilt:
1/(1+n*h) < 1/q ≤ p/q , Qed 2.Fall
3. Fall -1<r<0 : setzen h=1/(-r) -1 , bei h>0 folgt: r= -1/(1+h), weil auch hier abs(r)=1/(1+h) ist, gilt das Gleiche wie unter 2.Fall. Qed 3.Fall
d. {rn} sei Folge mit:
rn=1+r+r²...+ rn-1
n-tes Glied abschätzen:
rn = 1 +r +r²...+rn-1
rn*r= r +r²...+rn-1 +rn
rn -rn*r = rn*(1-r) = 1+rn
=> rn= (1+rn)/(1-r)
Man sieht sofort, dass der Limes =1/(1-r) ist.
δ-Kriterium mit Limes abschätzen:
abs(rn - 1/(1-r) ) < p/q
abs((1+rn)/(1-r) - 1/(1-r) ) < p/q
Für abs(r) <1 gilt:
1/(1-r) *abs(rn) < p/q
Mit δ' und N'δ ist die Konvergenz-Bedingung erfüllt.
e) Allg. Potenz-Reihe für rat.Zahl r
Wir bilden die Reihe rn aus d) neu:
Rn = r +r²... + rn
Rn*r= r²... + rn + rn+1
=> Rn -Rn*r = r + rn+1
=> Rn = (r + rn+1) /(1-r)
=> Rn = (1 + 1/bn+1) / (b-1)
=> R = a* [1/b +1/b² +1/b³ +...] =a/(b-1) ,a=1
Setzen wir a=p und b=q+1 so erhalten wir:
Satz1: über abzählbare Mengen
Alle rat. Zahlen p/q lassen sich als (unendl.) Potenzreihe der Form:
p/q =p* [1/(q+1) +1/(q+1)² +...] darstellen.
f) Dez.-Ziffern-Darstell. als Spez.Fall von rn
In rn = 1 +r +r²...+rn-1 r durch 1/p ersetzen:
rn = 1 +1/p +1/p²...+1/pn-1
= p(1 +1/pn)/(p-1)
rn = 1/p +1/p²...+1/pn-1 = (1 +1/pn)/(p-1)
Setzt man p=10, so bekommt man die bekannte Dez.Darstellung von rn= 1/9 auf n-1 Stellen nach Komma +(rat.)Restglied:
1/9 =1/10 +1/10²...+1/10n-1 +1/(9*10n)
bei n=∞: 1/9 =0,1111...1... (Zykl.)
Folgerung:
r =(p-1) *[1/p +1/p²...+1/p∞] =(p-1)/(p-1) =1
Wenn man q1,q2,q3..->∞ alle=1 setzt, folgt:
1 =(p-1) *[q1/p +q2/p²... ] ,für p>0
Sind nun alle Koeff. qn ,n=1,2,... verschieden (ohne Zyklus) ,so erhält man eine unendl. Potenz-Reihe aus rat. Elementen, wobei der Grenzwert keine rationale Zahl mehr ist!
Aussage 1:
Die Partialsummen der Reihen R in Satz 1 bilden eine konvergente Folge. Daraus kann man schlußfolgern: Alle rat. Zahlen sind Grenzwert und damit Häufungspunkt in der Menge M.
Aussage 2:
Die Grenzwerte von Potenzreihen mit rat. Elementen sind nur bei endl. vielen Gliedern (o. Zykl.) selbst wieder rat.Zahlen, ansonsten irrat. Zahlen.
Aussage 3:
Jede Dez.-Ziffern-Darstell. mit endlich vielen Stellen rechts vom Komma bezeichnet umkehrbar eindeutig eine rat.Zahl.
3.4 Sätze über konvergente Folgen:
Satz 1: Der Limes einer konvergenten Folge ist eindeutig.
D.h. das delta-, n-delta-Kriterium kann kann mit einer Zahl r erfüllt werden.
Beweis indirekt:
Seien a,b und b>a 2 Grenzwerte einer konvergenten Folge {rn} , dann kann man die delta-Umgebungen von a und b so klein wählen, daß sie Punkt-fremd sind. So würde der Abstand aller Punkte zum Grenzwert nicht Null werden, was im Widerspruch zur Konvergenz aller Pkte zu einem Grenzwert steht.
Satz 2: Gegeben seien 2 Zahlen r,r' und die zugehörigen Folgen {rn} , {r'n}. Dann ist die Folge {rn -r'n } genau dann eine Null-Folge, wenn r=r' ist, also r=r' <=> Limes{rn -r'n} =0
Satz 3: Jede rat. Zahl ist Grenzwert einer Folge, also Häufungspunkt in R.
Beweis konstruktiv:
Es sei r=p/q ,p,q∈G, q≠0 , dann ist rn=(p-1/n)/q und {rn}, n->unendl. eine konvergente Folge, deren Grenzwert p/q ist (entspr. Abschnitt 3.3 zuvor).
Qed.
Definition von Fundamental-Folgen: Eine Folge von rat. Zahl , später als "Elemente mit Abstand" bezeichnet, heißt Fundamentalfolge , wenn 2 Indizes n,m zu einem vorgegeb. delta>0, (später allg. Element "norm(delta)"), existieren, so daß gilt:
δ>0 vorgeb. =>∃N: abs(rn - rm)<δ ∀n,m≥N
(Sprachlich: Der Abstand zwischen 2 beliebigen Elementen kann beliebig klein gemacht werden.)
Folgerung1: Jede rat. Zahl r ist Grenzwert einer Fundam.Folge, also Repräsentant aller Folgen, die r als Grenzwert haben. Man sagt auch: Die Menge R ist vollständig, jedes Element kann über Fundamental-Folgen erreicht werden.
Diese Aussage ist enorm wichtig, weil später in den Modellen von Abbild. zwischen abstrakten Mengen die Begriffe Stetigkeit, Differenzierbarkeit, usw. über Fundam.Folgen def. werden.
Folgerung2: Nicht jede Fundamental-Folge hat als Grenzwert eine rat.Zahl oder ist eine rat.Zahl.
Beweis indirekt:
In Abschnitt 1.13 hatten wir im Ausdruck dn=2 festgestellt,dass d keine rat.Zahl ist. Wir fragen also umgekehrt: "Existiert eine rat.Zahl, die mit sich selbst mult. 2 ergibt?"
Es müßte also gelten: p/q *p/q =2 =>(p/q)=2*p/q , was im Widerspruch zur Teilerfremdheit von p zu q steht!
Satz4: Jede irrat.Zahl ist auch Grenzwert einer Fundamental-Folge von rat.Zahlen
Beweis konstruktiv:
r sei beliebige Zahl (auch irrat.), dann bilden wir 2 Folgen {a(n)} und {a'(n)}, von denen alle Elemente einmal unterhalb r liegen ,a(n), und bei a'(n) alle Elemente oberhalb von r liegen. Ist die Diff.-Folge {a(n)-a'(n)} eine Null-Folge, so sind nach Satz2 zuvor beide Grenzwerte gleich und r liegt dazwischen, also auch gleich!
1.Folge a(n):
1. Schritt: a1= a +b1/101 in allen Schritten bi so groß wählen,
daß ai<r bleibt
. . .
n. Schritt: a(n)= a(n-1) +b(n)/10n
Für beliebiges m>n setzen wir c=max(a(n-1), b(n), -a(m-1), -b(m)) und bilden:
abs(a(n)-a(m)) =c*(1+1/10n -1 -1/10m)
wegen m>n ist m=n+k, k ganz, k>0 :
=> abs(a(n)-a(m)) =c*(1+1/10n -1 -1/10n+k)
=> abs(a(n)-a(m)) =c*( (1/10n) *(1 -1/10k))
für belieb.k>0, also k→∞ :
=> abs(a(n)-a(m)) =c*( (1/10n) *(1 -0)
=> { abs(a(n)-a(m)) } ist Null-Folge, also {a(n)} konv.
2.Folge a'(n):
a'(n) bilden, wie a(n) zuvor, nur in allen Schritten b(i) so wählen, daß a'(i)>r bleibt.
a'(n) ist jetzt eine Folge, bei der alle Elemente oberhalb von r liegen.
abs(a(n)-a'(m)) wird wie zuvor gebildet m>n:
=> abs(a(n)-a'(m)) =c'*(1+1/10n -1 -1/10n+k)
=> abs(a(n)-a'(m)) =c*( (1/10n) *(1 -0)
=> { abs(a(n)-a'(m)) } ist Null-Folge, also {a(n)-a'(n)} konv.
Ergebnis: gleiche Grenzwerte, wie oben behauptet.
Ende Beweis Satz4
Definition reelle Zahlen: Die Menge aller Äquivalenzklassen, also Folgen gleicher Grenzwerte, von rat. Fundamental-Folgen bilden eine neue Menge R, genannt reelle Zahlen, die voll die Menge der rat. Zahlen umfaßt und aus allen rat.- und irrat.-Zahlen besteht.
Folgerung: Da die rat.Elemente einer Fundamental-Folge durch elementare Rechen-Operationen (Add/Sub/Mult/Div) hin und her geschoben werden können, wird auch der Grenzwert mit bewegt, so dass Add/Sub/Mult/Div auch für die Grenzwerte gilt.
Beweis indirekt:
Seien a,b und b>a 2 Grenzwerte einer konvergenten Folge {rn} , dann kann man die delta-Umgebungen von a und b so klein wählen, daß sie Punkt-fremd sind. So würde der Abstand aller Punkte zum Grenzwert nicht Null werden, was im Widerspruch zur Konvergenz aller Pkte zu einem Grenzwert steht.
Satz 2: Gegeben seien 2 Zahlen r,r' und die zugehörigen Folgen {rn} , {r'n}. Dann ist die Folge {rn -r'n } genau dann eine Null-Folge, wenn r=r' ist, also r=r' <=> Limes{rn -r'n} =0
Satz 3: Jede rat. Zahl ist Grenzwert einer Folge, also Häufungspunkt in R.
Beweis konstruktiv:
Es sei r=p/q ,p,q∈G, q≠0 , dann ist rn=(p-1/n)/q und {rn}, n->unendl. eine konvergente Folge, deren Grenzwert p/q ist (entspr. Abschnitt 3.3 zuvor).
Qed.
Definition von Fundamental-Folgen: Eine Folge von rat. Zahl , später als "Elemente mit Abstand" bezeichnet, heißt Fundamentalfolge , wenn 2 Indizes n,m zu einem vorgegeb. delta>0, (später allg. Element "norm(delta)"), existieren, so daß gilt:
δ>0 vorgeb. =>∃N: abs(rn - rm)<δ ∀n,m≥N
(Sprachlich: Der Abstand zwischen 2 beliebigen Elementen kann beliebig klein gemacht werden.)
Folgerung1: Jede rat. Zahl r ist Grenzwert einer Fundam.Folge, also Repräsentant aller Folgen, die r als Grenzwert haben. Man sagt auch: Die Menge R ist vollständig, jedes Element kann über Fundamental-Folgen erreicht werden.
Diese Aussage ist enorm wichtig, weil später in den Modellen von Abbild. zwischen abstrakten Mengen die Begriffe Stetigkeit, Differenzierbarkeit, usw. über Fundam.Folgen def. werden.
Folgerung2: Nicht jede Fundamental-Folge hat als Grenzwert eine rat.Zahl oder ist eine rat.Zahl.
Beweis indirekt:
In Abschnitt 1.13 hatten wir im Ausdruck dn=2 festgestellt,dass d keine rat.Zahl ist. Wir fragen also umgekehrt: "Existiert eine rat.Zahl, die mit sich selbst mult. 2 ergibt?"
Es müßte also gelten: p/q *p/q =2 =>(p/q)=2*p/q , was im Widerspruch zur Teilerfremdheit von p zu q steht!
Satz4: Jede irrat.Zahl ist auch Grenzwert einer Fundamental-Folge von rat.Zahlen
Beweis konstruktiv:
r sei beliebige Zahl (auch irrat.), dann bilden wir 2 Folgen {a(n)} und {a'(n)}, von denen alle Elemente einmal unterhalb r liegen ,a(n), und bei a'(n) alle Elemente oberhalb von r liegen. Ist die Diff.-Folge {a(n)-a'(n)} eine Null-Folge, so sind nach Satz2 zuvor beide Grenzwerte gleich und r liegt dazwischen, also auch gleich!
1.Folge a(n):
1. Schritt: a1= a +b1/101
. . .
n. Schritt: a(n)= a(n-1) +b(n)/10n
Für beliebiges m>n setzen wir c=max(a(n-1), b(n), -a(m-1), -b(m)) und bilden:
abs(a(n)-a(m)) =c*(1+1/10n -1 -1/10m)
=> abs(a(n)-a(m)) =c*(1+1/10n -1 -1/10n+k)
=> abs(a(n)-a(m)) =c*( (1/10n) *(1 -1/10k))
=> abs(a(n)-a(m)) =c*( (1/10n) *(1 -0)
=> { abs(a(n)-a(m)) } ist Null-Folge, also {a(n)} konv.
2.Folge a'(n):
a'(n) bilden, wie a(n) zuvor, nur in allen Schritten b(i) so wählen, daß a'(i)>r bleibt.
a'(n) ist jetzt eine Folge, bei der alle Elemente oberhalb von r liegen.
abs(a(n)-a'(m)) wird wie zuvor gebildet m>n:
=> abs(a(n)-a'(m)) =c'*(1+1/10n -1 -1/10n+k)
=> abs(a(n)-a'(m)) =c*( (1/10n) *(1 -0)
=> { abs(a(n)-a'(m)) } ist Null-Folge, also {a(n)-a'(n)} konv.
Ergebnis: gleiche Grenzwerte, wie oben behauptet.
Definition reelle Zahlen: Die Menge aller Äquivalenzklassen, also Folgen gleicher Grenzwerte, von rat. Fundamental-Folgen bilden eine neue Menge R, genannt reelle Zahlen, die voll die Menge der rat. Zahlen umfaßt und aus allen rat.- und irrat.-Zahlen besteht.
Folgerung: Da die rat.Elemente einer Fundamental-Folge durch elementare Rechen-Operationen (Add/Sub/Mult/Div) hin und her geschoben werden können, wird auch der Grenzwert mit bewegt, so dass Add/Sub/Mult/Div auch für die Grenzwerte gilt.
3.5 Rechnen mit reellen Zahlen:
Gegeben seien 2 reelle Zahlen a,b und zug. Fundamental-Folgen {r(n)} und {r'(n)}
Definition: Unter a+b , a*b versteht man diejenige reelle Zahl, die
durch {r(n)+r'(n)} bzw. {r(n)*r'(n)} , n=1,2,... dargestellt wird.
Damit die Definition sinnvoll ist, muß man nachweisen, daß
a) {r(n)+r'(n)} bzw. {r(n)*r'(n)} Fundamental-Folgen sind.
b) Die Definition von der spez. Wahl der Folge unabhängig. ist und
c) man mit Fundamental-Folgen genauso wie mit rat. Grenzwerten rechnen kann und dies zum gleichen Ergebnis führt.
Daß die 3 Ford. erfüllt sind soll exemplarisch an der Multiplikation gezeigt werden:
zu c) {r(n)}->r und {r'(n)}->r' rational => {r(n)*r'(n)} = {r*r'(n)} = r*r' Die Logik ist für rat. Zahlen trivial, abd nicht für irrat. Zahlen.
zu a)
rnr'n - rmr'm = rn(r'n - r'm) +r'm(rn - rm)
abs(rnr'n -rmr'm) = abs(rn)abs(r'n -r'm) +abs(r'm)abs(rn -rm)
Alle Elem. sind beschränkt abs(rn)≤k , abs(r'n)≤k'
Sei δ>0 vorgegeben,dann ∃N1,N2 so, daß gilt:
∀n,m≥N1: abs(rn -rm) <δ/(2k')
∀n,m≥N2: abs(r'n -r'm) <δ/(2k)
=> für N3=max(N1,N2):
abs(rnr'n -rmr'm)< k*δ/(2k) +k'*δ/(2k') =δ , ∀n,m≥N3
Das zeigt: {r(n)*r'(n)} ist Fundamental-Folge.
zu b) {r°(n)} und {r°'(n)} seien 2 andere Folgen aus den jeweiligen Äquivalenzklassen v. Folgen, die für die reellen Zahlen r und r' stehen. dann bilden die Folgen-Elemente (r(n)-r°(n)) und (r'(n)-r°'(n)) eine Null-Folge nach Satz2 Abschnitt 3.4 und die Grenzwerte sind gleich, d.h., man kann den Beweis zu a) auch mit diesen Folgen vornehmen.
Folgerung1: Gegeben seien 2 Folgen {r(n)}->r ,{r'(n)}->r' und die Diff.-Folge {r(n)-r'(n)} ist keine Null-Folge, also r≠r', dann kann die Relation r>r' oder r'>r abgeleitet werden.
Beweis: Ab einen hinreichend großen Index n sind in den jeweiligen δ-Umgeb. von r und r' keine Punkte der anderen Umgeb. mehr enthalten, so daß man aus den zugelassenen Relationen (größer,kleiner) der Elemente auch auf die entspr. Relationen der Grenzwerte schließen kann.
Folgen von reellen Zahlen:
Satz1: Zu Fundamental-Folgen
Gegeben sei eine Fundamental-Folge {r(n)} und eine δ-Umgeb. zu jedem Index &delta(n). Wenn die Folge {&delta(n)} selbst eine Null-Folge bildet, z.B. durch &delta(n)=1/n , dann ist jede weitere Folge {r'(n)} auch konvergent, wenn
r'm ∈ Uδ(n)(rn) m =hinreichend groß
ist.
Beweis: Durch die vorigen Aussagen +Folgerungen über Konvergenz-Verhalten von Folgen, ist dieser Satz hinreichend plausibel.
Wir haben den Satz1 vorangestellt, weil man sich die Elem. r(n) in den Folgen durch Fundamental-Folgen in den δ-Umgebungen zu r(n) ersetzt denken kann und die nachfolgenden Definitionen dadurch folgerichtiger erscheinen.
Definition von Folgen reeller Zahlen:
{r(n)} sei Folge beliebiger reeller Zahlen, dann gelten folg. Aussagen:
a) Die Folge heißt beschränkt, wenn gilt:
∃k>0: abs(r(n))≤k ,∀n
b) Die Folge heißt konverg., wenn es ein r gibt mit:
δ>0 =>∃N: abs(r(n)-r)<δ ,∀n≥N
c) Die Folge heißt Fundamental-Folge., wenn gilt:
δ>0 =>∃N: abs(rn-rm)<δ ,∀n,m≥N
Wie für rat.Zahlen gelten folg. Aussagen:
Satz2: Der Limes einer konv. Folge ist eindeutig.
Satz3: Ist {rn} konvergent, dann ist {rn} Fundamental-Folge.
Beweis: Es gilt z.B. abs( r(n) -r) <δ/2
=> rn-rm = (rn-r) +(r-rm) , ist m>n dann
=> abs(rn-rm) ≤absrn-r) +abs(r-rm) <δ/2 +δ/2 =δ
Satz4: Eine Fundamental-Folge ist auch beschränkt.
Satz5: {r(n)} ,{r'(n) konverg., dann sind auch:
a) { r(n) + r'(n) } konverg.-> r+r'
b) { r(n) *r'(n) } konverg.-> r*r'
b) { r(n)/r'(n) } konverg.-> r/r'für r'(n) ≠ 0
Beisp.:lim[(1-n+2n²)/(2+3n²)] =2/3
= (1/n²-1/n+2)/(2/n²+3)]
= (→0 -0 +2)/(→0 +3) =2/3
Satz6: r(n) ≤ r'(n) ,∀n≥N => r≤r'
Insbesondere gilt: r(n) ≤k => r ≤k
Satz7: In Verbindung mit Folgerung2 aus 3.4 gilt: Eine reelle Zahl kann durch Folgen rat. Zahlen beliebig angenähert =approximiert werden.
Damit die Definition sinnvoll ist, muß man nachweisen, daß
a) {r(n)+r'(n)} bzw. {r(n)*r'(n)} Fundamental-Folgen sind.
b) Die Definition von der spez. Wahl der Folge unabhängig. ist und
c) man mit Fundamental-Folgen genauso wie mit rat. Grenzwerten rechnen kann und dies zum gleichen Ergebnis führt.
Daß die 3 Ford. erfüllt sind soll exemplarisch an der Multiplikation gezeigt werden:
zu c) {r(n)}->r und {r'(n)}->r' rational => {r(n)*r'(n)} = {r*r'(n)} = r*r' Die Logik ist für rat. Zahlen trivial, abd nicht für irrat. Zahlen.
zu a)
rnr'n - rmr'm = rn(r'n - r'm) +r'm(rn - rm)
abs(rnr'n -rmr'm) = abs(rn)abs(r'n -r'm) +abs(r'm)abs(rn -rm)
Alle Elem. sind beschränkt abs(rn)≤k , abs(r'n)≤k'
Sei δ>0 vorgegeben,dann ∃N1,N2 so, daß gilt:
∀n,m≥N1: abs(rn -rm) <δ/(2k')
∀n,m≥N2: abs(r'n -r'm) <δ/(2k)
=> für N3=max(N1,N2):
abs(rnr'n -rmr'm)< k*δ/(2k) +k'*δ/(2k') =δ , ∀n,m≥N3
Das zeigt: {r(n)*r'(n)} ist Fundamental-Folge.
zu b) {r°(n)} und {r°'(n)} seien 2 andere Folgen aus den jeweiligen Äquivalenzklassen v. Folgen, die für die reellen Zahlen r und r' stehen. dann bilden die Folgen-Elemente (r(n)-r°(n)) und (r'(n)-r°'(n)) eine Null-Folge nach Satz2 Abschnitt 3.4 und die Grenzwerte sind gleich, d.h., man kann den Beweis zu a) auch mit diesen Folgen vornehmen.
Folgerung1: Gegeben seien 2 Folgen {r(n)}->r ,{r'(n)}->r' und die Diff.-Folge {r(n)-r'(n)} ist keine Null-Folge, also r≠r', dann kann die Relation r>r' oder r'>r abgeleitet werden.
Beweis: Ab einen hinreichend großen Index n sind in den jeweiligen δ-Umgeb. von r und r' keine Punkte der anderen Umgeb. mehr enthalten, so daß man aus den zugelassenen Relationen (größer,kleiner) der Elemente auch auf die entspr. Relationen der Grenzwerte schließen kann.
Folgen von reellen Zahlen:
Satz1: Zu Fundamental-Folgen
Gegeben sei eine Fundamental-Folge {r(n)} und eine δ-Umgeb. zu jedem Index &delta(n). Wenn die Folge {&delta(n)} selbst eine Null-Folge bildet, z.B. durch &delta(n)=1/n , dann ist jede weitere Folge {r'(n)} auch konvergent, wenn
ist.
Beweis: Durch die vorigen Aussagen +Folgerungen über Konvergenz-Verhalten von Folgen, ist dieser Satz hinreichend plausibel.
Wir haben den Satz1 vorangestellt, weil man sich die Elem. r(n) in den Folgen durch Fundamental-Folgen in den δ-Umgebungen zu r(n) ersetzt denken kann und die nachfolgenden Definitionen dadurch folgerichtiger erscheinen.
Definition von Folgen reeller Zahlen:
{r(n)} sei Folge beliebiger reeller Zahlen, dann gelten folg. Aussagen:
a) Die Folge heißt beschränkt, wenn gilt:
b) Die Folge heißt konverg., wenn es ein r gibt mit:
c) Die Folge heißt Fundamental-Folge., wenn gilt:
Wie für rat.Zahlen gelten folg. Aussagen:
Satz2: Der Limes einer konv. Folge ist eindeutig.
Satz3: Ist {rn} konvergent, dann ist {rn} Fundamental-Folge.
Beweis: Es gilt z.B. abs( r(n) -r) <δ/2
=> rn-rm = (rn-r) +(r-rm) , ist m>n dann
=> abs(rn-rm) ≤absrn-r) +abs(r-rm) <δ/2 +δ/2 =δ
Satz4: Eine Fundamental-Folge ist auch beschränkt.
Satz5: {r(n)} ,{r'(n) konverg., dann sind auch:
a) { r(n) + r'(n) } konverg.-> r+r'
b) { r(n) *r'(n) } konverg.-> r*r'
b) { r(n)/r'(n) } konverg.-> r/r'
Beisp.:
= (1/n²-1/n+2)/(2/n²+3)]
= (→0 -0 +2)/(→0 +3) =2/3
Satz6: r(n) ≤ r'(n) ,∀n≥N => r≤r'
Insbesondere gilt: r(n) ≤k => r ≤k
Satz7: In Verbindung mit Folgerung2 aus 3.4 gilt: Eine reelle Zahl kann durch Folgen rat. Zahlen beliebig angenähert =approximiert werden.
3.6 Eigenschaften der spez.Potenz-Reihe Pk(x)
a) Pk(x)= x/k +x/k² +...+x/kn+.. , wegen des Konverg.-Kriteriums
abs(x)<k , wird k auch als Konvergenz-Radius der Potenz-Reihe
Pk bezeichnet. Alle Potenz-Reihen dieser Form besitzen einen Konvergenz-Radius
, d.h., für alle Elemente innerhalb k ist Pk existent und definiert, sonst
nicht.
Definition (geometrische Folge/Reihe): Wir setzen a(n)=(x/k)n , dann ist das Verhältnis oder Quotient benachbarter Elemente der Folge {a(n)} konstant, nämlich x/k. Folge {a(n)} heißt deshalb "geometrische Folge"
Die zugehörige Potenz-Reihe P= a1 +a2 +.. +a(n) heißt dann "geometrische Reihe".
b) Die der Potenz-Reihe Pk zugrunde liegende geometrische Folge {a(n)} hat die Eigenschaft:
a(n) =a(n-1)*x/k ,∀n>1
=> a(n+1)/a(n) = a(n)/a(n-1)
=> a(n+1)*a(n-1) = a(n)² oder:
sqrt(a(n+1)*a(n-1)) = a(n)
Diese Eigenschaft wird geoetr. Mittel genannt im Gegensatz zum arithmet. Mittel:
1/2 *[(a(n+1) -a(n-1) ] =a(n)
c) Beispiel:
Bild , Reell-1.jpg
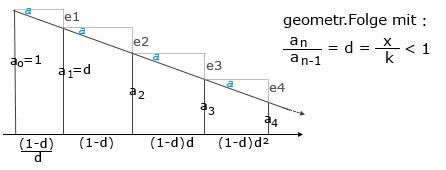
(a(2)-a(3))/(1-d)d = (a(2)-a(2)d)/(1-d)d
= (a(1)d -a(1)d²)/(1-d)d =a(1)
Gesamtsumme:
e1+...e(n) =a0-a1 +(a1-a2)+..+(a(n-1)-a(n)) = a0-a(n)
Wenn d=(k-1)/k ist, dann ist Limes(a0 -d∞) = a0 -0 =1 , also die klassische Teilung des Eins-Elementes bezüglich Teiler k.
d) Verallg. der Eins-Element-Teilung:
Eins =(k-1)/k +(k-1)/k² +...+(k-1)/kn+.. ist spez. Fall einer allg. Form: P(r) = 1+r +r² +... +rn +... ,1>abs(r)
Diese Potenz-Reihen basieren auf Folgen der Form: a0=1, a1=r, a2=a1*r, a(n)=a(n-1)*r. abs(r)<1 steht hier für den sog. Konvergenz-Radius, so daß P(r) auch in der Form P(x/k) konvergiert, wenn x=reell u. abs(r)<k ist.
Entspr. "Abschnitt 3.3 f)" ist der Grenzwert:
P(x/k)= (1 +(x/k)n)/(1-x/k)
Beispiel: P(1/2) =(1-0) / (1-1/2) = 2
Folgerung: Mit P(x/k) ,abs(r)<k, x=reell, k=ganz. hat man eine greifbare Darstellung für alle reelle Zahlen innerhalb einer Umgebung um Null mit Radius k, dabei gilt:
Für rat.Zahlen= exakte Darstell. gleichberechtigt neben p/q
Für irrrat.Zahlen= eine Darstell. mit belieb. Genauigkeit n→∞.
Problem: Will ich für ein allg. x=reell. eine konvergente Reihe konstruieren, so müßte das k immer angepaßt werden, also variabel sein. Die Lösung liegt im Ansatz: statt a(n)=a(n-1)*x/k wird a(n)=a(n-1)+x/n gesetzt!
n=1: a(1) = a0 *x1/1a0 = x0 =1
n=2: a(2) = a0 *x²/(1*2)
n=3: a(3) = a0 *x³/(1*2*3)
. . . .
n=n: a(n) = a0 *xn/(1*2*3)
n=n+1: a(n+1) = a0 *x(n+1)/(n+1)!
=> P(x)= a0 +a1 +a2 +... +a(n)
=> P(x)= 1 +x +x²/2! +x³/3! ... +x(n+1)/(n+1)!
P(x) konvergiert für alle x=reell.
Beweis:
1. Die a(n) sind monoton steigend:
a(n+1)/(n+1)! =(a(n)/n!) *n/(n+1) >a(n)/n!
2. Abschätzen für x=1:
P(1)= 1 +1 +1²/2! +1³/3! ... +1(n)/n! +..
P(1)< 1 +1 +1²/2² +1³/3³ ... +1/2(n) +..
Ab Index n=2 sind die Elemente 1/2(n) größer, so daß ab der 2-ten 1 gilt: P(1)<2 und mit Erster 1 zusammen P(1)<3, mindestens aber: 1 +1 +1/2 =2.5 , d.h.,wir haben für P(1) folg.Abschätzung:
2.5 <P(1) <3
Diese spez. irrat.Zahl ~ 2,71828... wird Eulersche Zahl genannt, sysmb: e
3. Abschätzen für x=0:
P(x=0)= 1 +x +x²/2! +x³/3! +... ==> P0)=1
4. Abschätzen für 1>x>-1:
Da die a(n) monoton wachsend sind, liegen die Zahlen zwischen P)0) und P(1) , also zwischen 1 und e.
5. Abschätzen für abs(x)>1:
Für den Beweis von x>1 muß nachgewiesen werden, daß ab hinreichend großem n(x) gilt: xn <n! , ∀x≥n(x).
a) für 2n/n!: 2n/n! <1/2n ,ab n≥9 (Ausprobieren)
b) für an/n!: 2k*n/n! <1/2n , ∀n≥k*9 , x≤a≤2k
6. Abschätzen für x->unendl.:
Ausklammern x aus P(x): 1 +x* (x/2! +x²/3! +...
Hier sieht man sofort, P(x)→+∞ für x→+∞
Für x gegen minus-unendl. kann an dieser Stelle noch keine Aussage gemacht werden.
Ende des Beweises
Definition (geometrische Folge/Reihe): Wir setzen a(n)=(x/k)n , dann ist das Verhältnis oder Quotient benachbarter Elemente der Folge {a(n)} konstant, nämlich x/k. Folge {a(n)} heißt deshalb "geometrische Folge"
Die zugehörige Potenz-Reihe P= a1 +a2 +.. +a(n) heißt dann "geometrische Reihe".
b) Die der Potenz-Reihe Pk zugrunde liegende geometrische Folge {a(n)} hat die Eigenschaft:
=> a(n+1)/a(n) = a(n)/a(n-1)
=> a(n+1)*a(n-1) = a(n)² oder:
sqrt(a(n+1)*a(n-1)) = a(n)
Diese Eigenschaft wird geoetr. Mittel genannt im Gegensatz zum arithmet. Mittel:
1/2 *[(a(n+1) -a(n-1) ] =a(n)
c) Beispiel:

= (a(1)d -a(1)d²)/(1-d)d =a(1)
Gesamtsumme:
e1+...e(n) =a0-a1 +(a1-a2)+..+(a(n-1)-a(n)) = a0-a(n)
Wenn d=(k-1)/k ist, dann ist Limes(a0 -d∞) = a0 -0 =1 , also die klassische Teilung des Eins-Elementes bezüglich Teiler k.
d) Verallg. der Eins-Element-Teilung:
Eins =(k-1)/k +(k-1)/k² +...+(k-1)/kn+.. ist spez. Fall einer allg. Form: P(r) = 1+r +r² +... +rn +... ,1>abs(r)
Diese Potenz-Reihen basieren auf Folgen der Form: a0=1, a1=r, a2=a1*r, a(n)=a(n-1)*r. abs(r)<1 steht hier für den sog. Konvergenz-Radius, so daß P(r) auch in der Form P(x/k) konvergiert, wenn x=reell u. abs(r)<k ist.
Entspr. "Abschnitt 3.3 f)" ist der Grenzwert:
Folgerung: Mit P(x/k) ,abs(r)<k, x=reell, k=ganz. hat man eine greifbare Darstellung für alle reelle Zahlen innerhalb einer Umgebung um Null mit Radius k, dabei gilt:
Für rat.Zahlen= exakte Darstell. gleichberechtigt neben p/q
Für irrrat.Zahlen= eine Darstell. mit belieb. Genauigkeit n→∞.
Problem: Will ich für ein allg. x=reell. eine konvergente Reihe konstruieren, so müßte das k immer angepaßt werden, also variabel sein. Die Lösung liegt im Ansatz: statt a(n)=a(n-1)*x/k wird a(n)=a(n-1)+x/n gesetzt!
n=1: a(1) = a0 *x1/1
n=2: a(2) = a0 *x²/(1*2)
n=3: a(3) = a0 *x³/(1*2*3)
. . . .
n=n: a(n) = a0 *xn/(1*2*3)
n=n+1: a(n+1) = a0 *x(n+1)/(n+1)!
=> P(x)= a0 +a1 +a2 +... +a(n)
=> P(x)= 1 +x +x²/2! +x³/3! ... +x(n+1)/(n+1)!
P(x) konvergiert für alle x=reell.
Beweis:
1. Die a(n) sind monoton steigend:
a(n+1)/(n+1)! =(a(n)/n!) *n/(n+1) >a(n)/n!
2. Abschätzen für x=1:
P(1)= 1 +1 +1²/2! +1³/3! ... +1(n)/n! +..
P(1)< 1 +1 +1²/2² +1³/3³ ... +1/2(n) +..
Ab Index n=2 sind die Elemente 1/2(n) größer, so daß ab der 2-ten 1 gilt: P(1)<2 und mit Erster 1 zusammen P(1)<3, mindestens aber: 1 +1 +1/2 =2.5 , d.h.,wir haben für P(1) folg.Abschätzung:
Diese spez. irrat.Zahl ~ 2,71828... wird Eulersche Zahl genannt, sysmb: e
3. Abschätzen für x=0:
P(x=0)= 1 +x +x²/2! +x³/3! +... ==> P0)=1
4. Abschätzen für 1>x>-1:
Da die a(n) monoton wachsend sind, liegen die Zahlen zwischen P)0) und P(1) , also zwischen 1 und e.
5. Abschätzen für abs(x)>1:
Für den Beweis von x>1 muß nachgewiesen werden, daß ab hinreichend großem n(x) gilt: xn <n! , ∀x≥n(x).
a) für 2n/n!: 2n/n! <1/2n ,ab n≥9 (Ausprobieren)
b) für an/n!: 2k*n/n! <1/2n , ∀n≥k*9 , x≤a≤2k
6. Abschätzen für x->unendl.:
Ausklammern x aus P(x): 1 +x* (x/2! +x²/3! +...
Hier sieht man sofort, P(x)→+∞ für x→+∞
Für x gegen minus-unendl. kann an dieser Stelle noch keine Aussage gemacht werden.
Folgerung:
Dies ist die wichtigste Aussage zu Zahlen im Modell der reellen Zahlen!
Mit P(x)= 1 +x +x²/2! +x³/3! +... haben wir eine Potenz-Reihen-Darstellung füralle Zahlen x=reell.(rat. +irrat.), wobei für rat.Zahlen auch der
Quotient p/q steht.
Die Näherung für irrat. Zahlen (n<∞) ist eine endl. Potenzreihe und kann nach Algorithmus im "Abschnitt 1.14 Eukl.Geometrie" problemlos in p/q umgewandelt werden und ist somit rational.
Dies ist die wichtigste Aussage zu Zahlen im Modell der reellen Zahlen!
Mit P(x)= 1 +x +x²/2! +x³/3! +... haben wir eine Potenz-Reihen-Darstellung für
Die Näherung für irrat. Zahlen (n<∞) ist eine endl. Potenzreihe und kann nach Algorithmus im "Abschnitt 1.14 Eukl.Geometrie" problemlos in p/q umgewandelt werden und ist somit rational.
3.7 Mehrfach-Multiplikation von Zahlen
a) (n+m)-Multiplikation einer Zahl:
r1 ***** rn+m = rn+m = rn*rm
rn/rm = rn-m Durch Kürzen bleiben (n-m) Stell.übrig
Ist n=0, folgt: 1/rm = r-m
Ist n=m, folgt: r0 =1
b) (n*m)-Multiplikation einer Zahl:
r1 ***** rn*m = rn**m** rn
= (rn)m = (rm)n = rn*m
rp * 1/rq = rp*1/q = rp/qp/q =ration. Exponent
c) Umkehr-Operation:
Ist n=m, folgt: rn*(1/rm) = rn/m =r1
↑n und ↑1/n sind also gegenseitige Umkehr-Operationen.
d) Schreibweise-Symbolik:
r1 **** rn = Potenz(r,n) =rn
1/(r1***rm) =Wurzel(m,r) =r-m
Bisher wurden Potenzen mit rat.Exponenten definiert. Um Potenzen für alle reellen Zahlen zu def., müssen wir irrat.Exponenten untersuchen.
Satz1:
Die Grenzwerte folg. 2 Ausdrücke sind gleich:
(1+1/n)n =1 +1 +1²/2! +1³/3! +... ,n→∞
Beweis:
Bild , Reell-2a.jpg

Bild , Reell-2b.jpg
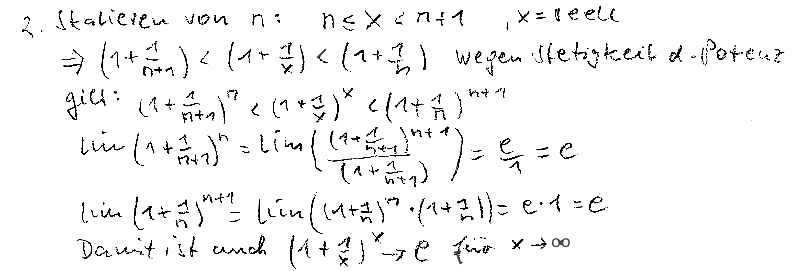
(1 +x/r)r =1 +x +x²/2! +x³/3! +... ,r→∞
Die Bedeutung diese Beziehung läßt sich jetzt leicht ermitteln:
Wir setzen y=r/x
=> (1 +1/y)y*x = [1 +1/y)y]x = ex, y→∞
Ende des Beweises
Beispiel:
(1+1/10000)10000 = 2,718 145927..
(1 +1/1Mio)1Mio = 2,71828 0469..
e= 2,71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 …
(1+2/10000)10000 = e2 =7,3875..
tatsächlich: e2 =7,38905..
e) Umkehr-Operation zu ex =exp(x):
Wegen Limes(1/±n)=0 ist auch der Ausdruck (1+±x/n)n>0 ,für n→∞ .Das bedeutet:
exp(x) ist für alle x def., -∞<x<+∞
und für exp(x) selbst: 0<exp(x)<+∞
Im Ausdruck: y=exp(x) ,x,y reell, gibt es also auch für x eine Potenz- Reihen-Darstellung, z.B. x=exp(y'). Diese heißt symb.: ln(), weil man mit x=ln(y) den Exponenten aus der Potenz exp(x) wiederherstellen kann. Damit das für alle y (=exp(x), x=reell) funktioniert, muß man nachweisen, daß alle Fundamental-Folgen in x auch in Fundamental-Folgen nach y abgebildet werden.
Satz1: x(i)=1/2i(a-x) ,i=1,2.. ,a=reell sei Fundamental-Folge in x, dann ist auch:
[1+(x-x(i)/n]n Fundamental-Folge:
[1+(x-x(i)/n]n= e(x-(a-x)/2i)
=ex , (n→∞)
d.h., exp{x(i)} ->exp(x) , i→∞
Damit gilt auch: ln{y(i)} ->ln(y), y(i)>0
Zusammenstellung:
Bild , Reell-3.jpg
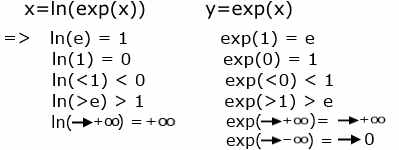
ax=eln(a)*x , a>0
r1 ***** rn+m = rn+m = rn*rm
rn/rm = rn-m
Ist n=0, folgt: 1/rm = r-m
Ist n=m, folgt: r0 =1
b) (n*m)-Multiplikation einer Zahl:
r1 ***** rn*m = rn
rp * 1/rq = rp*1/q = rp/q
c) Umkehr-Operation:
Ist n=m, folgt: rn*(1/rm) = rn/m =r1
d) Schreibweise-Symbolik:
r1 **** rn = Potenz(r,n) =rn
1/(r1***rm) =Wurzel(m,r) =r-m
Bisher wurden Potenzen mit rat.Exponenten definiert. Um Potenzen für alle reellen Zahlen zu def., müssen wir irrat.Exponenten untersuchen.
Satz1:
Die Grenzwerte folg. 2 Ausdrücke sind gleich:
Beweis:

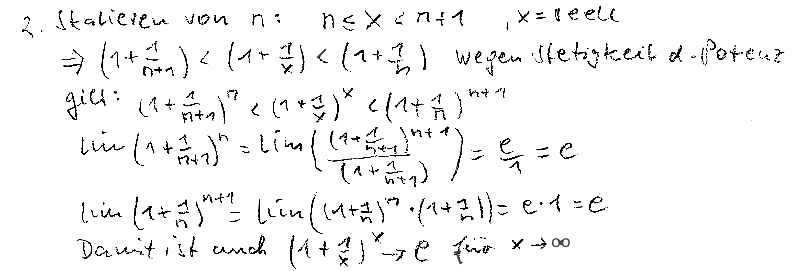
(1 +x/r)r =1 +x +x²/2! +x³/3! +... ,r→∞
Die Bedeutung diese Beziehung läßt sich jetzt leicht ermitteln:
Wir setzen y=r/x
=> (1 +1/y)y*x = [1 +1/y)y]x = ex
Beispiel:
e) Umkehr-Operation zu ex =exp(x):
Wegen Limes(1/±n)=0 ist auch der Ausdruck (1+±x/n)n>0 ,für n→∞ .Das bedeutet:
exp(x) ist für alle x def., -∞<x<+∞
und für exp(x) selbst: 0<exp(x)<+∞
Im Ausdruck: y=exp(x) ,x,y reell, gibt es also auch für x eine Potenz- Reihen-Darstellung, z.B. x=exp(y'). Diese heißt symb.: ln(), weil man mit x=ln(y) den Exponenten aus der Potenz exp(x) wiederherstellen kann. Damit das für alle y (=exp(x), x=reell) funktioniert, muß man nachweisen, daß alle Fundamental-Folgen in x auch in Fundamental-Folgen nach y abgebildet werden.
Satz1: x(i)=1/2i(a-x) ,i=1,2.. ,a=reell sei Fundamental-Folge in x, dann ist auch:
d.h., exp{x(i)} ->exp(x) , i→∞
Damit gilt auch: ln{y(i)} ->ln(y), y(i)>0
Zusammenstellung:
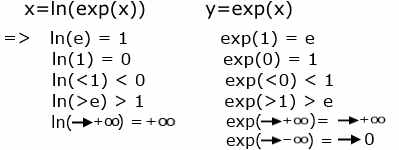
Zusammenfassung:
Zu allen reellen Zahlen sind die Verknüpfungen: Add/Sub Mult/Div und Potenz(), sowie die Umkehr-Funktionen: Wurzel() und ln(x>0) def.
Die reellen Zahlen bilden damit einen vollständigen Raum und sind somit Grundlage der n-dim Eukl. Zahlen-Räume.
Zu allen reellen Zahlen sind die Verknüpfungen: Add/Sub Mult/Div und Potenz(), sowie die Umkehr-Funktionen: Wurzel() und ln(x>0) def.
Die reellen Zahlen bilden damit einen vollständigen Raum und sind somit Grundlage der n-dim Eukl. Zahlen-Räume.
3.8 Beispiel für Wachstums-Folge
a) Ruckweises Wachstum:
Ausgangspunkt ist a0. Im nächsten Schritt wird a0 um einen prozentualen Anteil von a0 erhöht usw.
a0
a1 = a0(1 +x/k)
. . . .
a(n) = a(n-1)(1 +x/k) , (geometr. Folge d=(1+x/k) )
=> an/a(n-1) * a2/a1 *a1/a0 = (1 +x/k)n
=> a0*Limes{a(i)} =unendl. ,1=1,2,....
Beispiel: Ein Kapital a0 wird mit 5%/Jahr verzinst. nach n=3 Jahren hat man:
a0 *(1.05)³ Endkapital. Nach 5 Monaten hat man:
a0 *(1.05)5 *1/12 =a0 *1.0205... Endkapital.
b) Kontinuierliches Wachstum:
Im zeitl. Ablauf der Natur treten häufig kontinuierliche, stetige oder mehr oder weniger gleichmäßig wachsende (o. fallende) Prozesse auf. Deshalb spricht man auch vom "natürlichen Wachstum" , z.B wächst ein Baum ununterbrochen.
Kennzeichnend für stetiges Wachstum ist, daß z.B. die Ausgangs-Menge ständig um einen bestimmten Faktor wächst oder schrumpft. Dieser Faktor kann zu jeder Zeit anders sein oder gleich, dann spricht man von einen gleichmäßigem Wachstum.
Faktor f=const.,dann ist Menge im Verhältnis von Schritt n zu n+1 um f=reell. gewachsen, bei 0>f geschrumpft. Die (gemetr.) Folge lautet:
{ a0(1+f/n)n } , n=1,2,... oder auch n=reell.,da auch extrem kleine Schritte (z.B. Zeit-Abschnitte->0) betrachtet werden können.
Die Folge ist uns bekannt als: (1+f/n)n =ef
Beispiel:
Das Kapital zuvor wurde nach 1Jahr mit 5% verzinst.
Jahres-%: a0*(1 +0.05/1 )1 = a0*1.05 (nach 1Jahr)
Monats-%: a0*(1 +0.05/12 )1*12=a0*1.05116..
Tages-%: a0*(1 +0.05/365 )1*365=a0*1.05126..
n→∞-%: a0*(1 +0.05/n )1*n=a0*e0.05=1.05127..
Ergebnis:
Das höchste Kapital erhalte ich bei kontinuierl., stetiger Verzinsung. Besonders macht sich das bei längerer Laufzeit bemerkbar:
30Jahre á5% = a0*(1 +0.05/1 )1*10 =a0*4.321 94..
30Jahre 5%stetig = a0*(e0.05)30 =a0*4.481 68..
Das sind 3.6% mehr.
c) Mehrere Kugeln in Tüte:
Bild , Reell-4.jpg
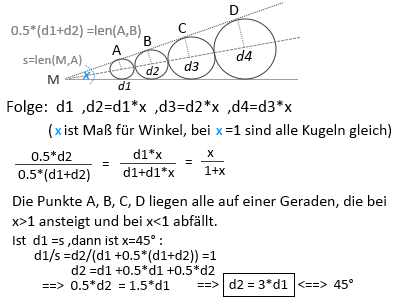
d) Abstufungs-Folge:
2 Rohre mit 20mm und 200mm Durchmesser. Gesucht wird Abstufung mit 4 weiteren dazwischen-liegenden Rohren, so daß sie in eine Tüte passen:
Bild , Reell-5.jpg
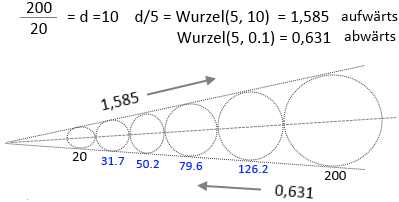
Die Abstufung ist Wurzel(5,10)= 1.585
d1 = 20
d2= 20 *1.585 = 31.7
d3= 31.7 *1.585 = 50.2
d4= 50.2 *1.585 = 79.6
d5= 79.6 *1.585 = 126.2
d6 = 200 = 126.2 *1.585
Ausgangspunkt ist a0. Im nächsten Schritt wird a0 um einen prozentualen Anteil von a0 erhöht usw.
a0
a1 = a0(1 +x/k)
. . . .
a(n) = a(n-1)(1 +x/k) , (geometr. Folge d=(1+x/k) )
=> an/a(n-1) * a2/a1 *a1/a0 = (1 +x/k)n
=> a0*Limes{a(i)} =unendl. ,1=1,2,....
Beispiel: Ein Kapital a0 wird mit 5%/Jahr verzinst. nach n=3 Jahren hat man:
a0 *(1.05)³ Endkapital. Nach 5 Monaten hat man:
a0 *(1.05)5 *1/12 =a0 *1.0205... Endkapital.
b) Kontinuierliches Wachstum:
Im zeitl. Ablauf der Natur treten häufig kontinuierliche, stetige oder mehr oder weniger gleichmäßig wachsende (o. fallende) Prozesse auf. Deshalb spricht man auch vom "natürlichen Wachstum" , z.B wächst ein Baum ununterbrochen.
Kennzeichnend für stetiges Wachstum ist, daß z.B. die Ausgangs-Menge ständig um einen bestimmten Faktor wächst oder schrumpft. Dieser Faktor kann zu jeder Zeit anders sein oder gleich, dann spricht man von einen gleichmäßigem Wachstum.
Faktor f=const.,dann ist Menge im Verhältnis von Schritt n zu n+1 um f=reell. gewachsen, bei 0>f geschrumpft. Die (gemetr.) Folge lautet:
{ a0(1+f/n)n } , n=1,2,... oder auch n=reell.,da auch extrem kleine Schritte (z.B. Zeit-Abschnitte->0) betrachtet werden können.
Die Folge ist uns bekannt als: (1+f/n)n =ef
Beispiel:
Das Kapital zuvor wurde nach 1Jahr mit 5% verzinst.
Jahres-%: a0*(1 +0.05/1 )1 = a0*1.05 (nach 1Jahr)
Monats-%: a0*(1 +0.05/12 )1*12=a0*1.05116..
Tages-%: a0*(1 +0.05/365 )1*365=a0*1.05126..
n→∞-%: a0*(1 +0.05/n )1*n=a0*e0.05=1.05127..
Ergebnis:
Das höchste Kapital erhalte ich bei kontinuierl., stetiger Verzinsung. Besonders macht sich das bei längerer Laufzeit bemerkbar:
30Jahre á5% = a0*(1 +0.05/1 )1*10 =a0*4.321 94..
30Jahre 5%stetig = a0*(e0.05)30 =a0*4.481 68..
Das sind 3.6% mehr.
c) Mehrere Kugeln in Tüte:

d) Abstufungs-Folge:
2 Rohre mit 20mm und 200mm Durchmesser. Gesucht wird Abstufung mit 4 weiteren dazwischen-liegenden Rohren, so daß sie in eine Tüte passen:

Die Abstufung ist Wurzel(5,10)= 1.585
d1 = 20
d2= 20 *1.585 = 31.7
d3= 31.7 *1.585 = 50.2
d4= 50.2 *1.585 = 79.6
d5= 79.6 *1.585 = 126.2
d6 = 200 = 126.2 *1.585
3.9 n-dim abstrakter Eukl. Raum
Definition1: Die Menge M aller n-Tupel reeller Zahlen heißt
abstrakter n-dim Eukl. Raum:
M ={(r1,...rn)} ,ri=reell
,symb: Rn
Definition2: Jede 1-dim Projektion des Rn1 ={(0,...ri...0)} , 1≤i≤n ist äquivalent zur Menge der reellen Zahlen R. Symb.: R1.
Axiomatik für Elemente des Rn:
Axiom1: Linearität von M, d.h., jede Linearkombination L() von Elementen ist wiederum Element von M (Rn):
L(p1,...,pm) =r1*p1+...+r(m)*p(m), rj=reell ,pj∈Rn
, 1≤j≤m
Für Verknüpfung L() gelten die Eigenschaften: kommutativ, assoziativ, distributiv, vollständig.
Die Vollständigkeit bedeutet: Zu jedem Element p kann ich irgendeine L()
angeben, so daß gilt: p=L() ,z.B. L(p1,p2)= r1*p1 + r2*p2 , r1,r2 geeignet gewählt.
Axiom2: Skalarprodukt:
Zwischen 2, nicht notwendig verschiedenen, Elementen p1,p2 wird ein Skalarprodukt, Symb: Skapro(p1,p2) oder <p1,p2> ,wie folgt definiert:
<p1,p2>= (x1*y1)+...+[x(n)*y(n)] p1=(x1,...,x(n) ) ,p2=(y1,...,y(n) )
Das Skapro() ist eine reelle Zahl und wird nur Null, wenn p1=Null oder p2=Null sind , (oder bei Rechtwinkl.).
Axiom3: Jedem Element a kann eine Norm() =reelle Zahl zugeordnet werden, indem man:
Norm(a)= abs(sqrt(<a,a>)) setzt.
Diese spez. Norm im Rn wird auch Euklidische Norm genannt.
Folgerung:
Interpretiert man ein Element, z.B. a, als Richtung von Null->Pkt.a , so erscheint Norm(a) wie als Maß für den Abstand von Null->a oder a->Null.
Es sei a,b∈Rn , c=reell , dann hat dieser Abstands-Begriff folg. Eigenschaften:
- Norm(a)≥0 ,=0 wenn a=Null
- Norm(c*a)=c*Norm(a)
- Norm(a±b)= Norm(b±a) ,=0 wenn a=b
- Norm(a+b)≤ Norm(a) +Norm(b)
Die letzte Eigenschaft (Dreiecks-Ungleichung) ist nicht so einfach einzusehen und macht, wenn sie stimmt, den Rn zu einem metrischen Raum.
Beweis für Gültigkeit d. Dreiecks-Ungleich.:
In der Folge wird der Abstand 2-er Elemente a,b mit d(a,b) bezeichnet. Sei a,b,c Elemente, dann soll gelten:
d(a,b)≤ d(a,c) +d(c,a)
Zuerst benötigen wir ein paar Hilfssätze:
Bild , Hilfsatz1.jpg
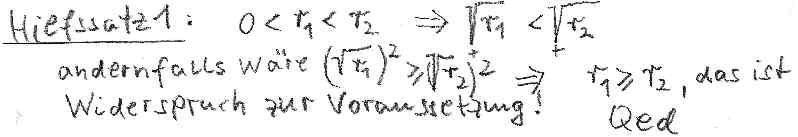
Bild , Hilfsatz2.jpg

Bild , Hilfsatz3.jpg

Fortführung des Beweises:
gegeben: 3 Elemente x1, x2, x3 dann seien:
a(i) = x3(i) -x1(i) ,
b(i) = x2(i) -x3(i) ,
a(i) +b(i) = x2(i) -x1(i) , nach Hilfssatz3 gilt:
d(x1,x2) =sqrt[Sum(a(i)+b(i))²]
≤ sqrt[Sum(a(i))²] +sqrt[Sum(b(i))²]
= d(x1,x3) +d(x3,x2)
Ende des Beweises (Dreiecks-Ungleichung)
Definition2: Jede 1-dim Projektion des Rn1 ={(0,...ri...0)} , 1≤i≤n ist äquivalent zur Menge der reellen Zahlen R. Symb.: R1.
Axiomatik für Elemente des Rn:
Axiom1: Linearität von M, d.h., jede Linearkombination L() von Elementen ist wiederum Element von M (Rn):
L(p1,...,pm) =r1*p1+...+r(m)*p(m)
, 1≤j≤m
Für Verknüpfung L() gelten die Eigenschaften: kommutativ, assoziativ, distributiv, vollständig.
Axiom2: Skalarprodukt:
Zwischen 2, nicht notwendig verschiedenen, Elementen p1,p2 wird ein Skalarprodukt, Symb: Skapro(p1,p2) oder <p1,p2> ,wie folgt definiert:
Das Skapro() ist eine reelle Zahl und wird nur Null, wenn p1=Null oder p2=Null sind , (oder bei Rechtwinkl.).
Axiom3: Jedem Element a kann eine Norm() =reelle Zahl zugeordnet werden, indem man:
Norm(a)= abs(sqrt(<a,a>)) setzt.
Diese spez. Norm im Rn wird auch Euklidische Norm genannt.
Folgerung:
Interpretiert man ein Element, z.B. a, als Richtung von Null->Pkt.a , so erscheint Norm(a) wie als Maß für den Abstand von Null->a oder a->Null.
Es sei a,b∈Rn , c=reell , dann hat dieser Abstands-Begriff folg. Eigenschaften:
- Norm(c*a)=c*Norm(a)
- Norm(a±b)= Norm(b±a) ,=0 wenn a=b
- Norm(a+b)≤ Norm(a) +Norm(b)
Die letzte Eigenschaft (Dreiecks-Ungleichung) ist nicht so einfach einzusehen und macht, wenn sie stimmt, den Rn zu einem metrischen Raum.
Beweis für Gültigkeit d. Dreiecks-Ungleich.:
In der Folge wird der Abstand 2-er Elemente a,b mit d(a,b) bezeichnet. Sei a,b,c Elemente, dann soll gelten:
d(a,b)≤ d(a,c) +d(c,a)
Zuerst benötigen wir ein paar Hilfssätze:
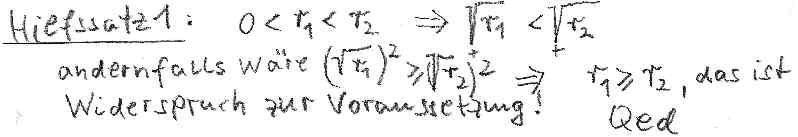


Fortführung des Beweises:
gegeben: 3 Elemente x1, x2, x3 dann seien:
a(i) = x3(i) -x1(i) ,
b(i) = x2(i) -x3(i) ,
a(i) +b(i) = x2(i) -x1(i) , nach Hilfssatz3 gilt:
d(x1,x2) =sqrt[Sum(a(i)+b(i))²]
≤ sqrt[Sum(a(i))²] +sqrt[Sum(b(i))²]
= d(x1,x3) +d(x3,x2)
3.10 Fundamental-Folgen im Rm
Definition δ-Umgebung:
x0∈Rm, dann heißt die Menge allr x, die von x0
einen Abstand d(x,x0)<δ haben, die "δ-Umgebung" von x0 , Symb.: Uδ(x0).
Bemerkung: Im R1 ist delta-Umgebung ein Intervall mit x0-δ <x< x0+δ.
Satz1: Mit jedem Pkt.x' der delta-Umg(x0) ist auch eine ganze delta-Umg(x') vollständig in delta(x0) enthalten, wenn δ' =δ -d(x',x0) ist.
Bild , Reell-6.jpg
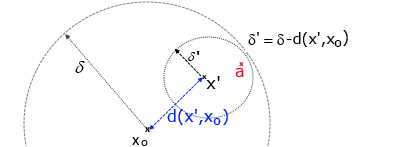
Beweis: a sei beliebiger Pkt. in delta'(x'), dann ist d(a,x')<δ'
=> d(a,x0) ≤ d(x',x0) +d(a,x') <d(x',x0)+δ'
=> d(x',x0)+δ' = d(x',x0) +(δ-d(x',x0)) =δ
Ende des Beweises
Definition Folgen im Rm:
Konvergenz:
{x(n)} sei Folge von Punkten x(n):
x(n) =( x(n)1, x(n)2,...x(n)m ) , dann heißt Folge {x(n)} konvergent, wenn es ein x*=(x(*)1, . . . , x(*)m ) mit einer beliebigen delta(x*)-Umg. gibt, so daß alle x(n) ab einem best.Index N>n innerhalb der delta(x*) liegen. (δ -Nδ' -Kriterium )
also: ∀n≥Nδ: d(x*,x(n) )<δDie Abstände bilden 0-Folge
Beschränktheit:
Eine Folge {x(n)} heißt beschränkt, wenn es ein k>0 gibt, so daß der Abstand zum Null-Pkt. ≤k ist, d(x((n),Null)≤k,∀n.
Fundamental-Folge:
Eine Folge {x(n)} heißt Fundamental-Folge, wenn gilt:
geg.δ>0 => ∃Nδ: d(x(n),x(k)) <δ , ∀n,k≥Nδ
Bemerkung: Wenn man den Grenzwert einer Folge nicht kennt, hilft
das δ-Nδ-Kriterium für beliebige Abstände innerhalb einer
Folge weiter!
Satz2: Ist {x(n)}->x* konvergent, dann gilt auch umgekehrt: {x(n)i}->x*i ,i=1,2,...,m
(m= Dimension des Rm)
Wenn Folge konvergent, dann auch die Folgen der einzelnen Koordinaten und umgekehrt.
Zuerst ein paar Hilfssätze:
Bild , Reell-7.jpg

Nach Hilfsaussage2 gilt dann: d(x(n),x*)=Sum[j](d(x(n)j,x(*)j)) <c*sqrt(m) , bei c=δ/sqrt(m) ist d(x(n),x*) <δ ∀n≥max(N1,...,N(m)).
Also gilt auch: x(n)->x*.
Ende des Beweises
Folgerung1: Der Limes einer konvergenten Folge im Rm ist eindeutig bestimmt, weil die Limes aus den j-ten Komponenten {x(n)j}->x(*)j eindeutig bestimmt sind.
Folgerung2: Eine konvergente Folge ist beschränkt, denn die d(x(n)j)≤k(j) sind beschränkt. Ist k=max(k(1),...,k(m)), so gilt auch:
d(x(n)j,Null) ≤k(j)) ≤k . Nach Hilfsaus.2 ist:
d(x(n)j,Null) ≤k*sqrt(m).
Folgerung3: Ist {x(n)} Fundamental-Folge, so ist {x(n)} ->konvergent.
x0∈Rm, dann heißt die Menge allr x, die von x0
einen Abstand d(x,x0)<δ haben, die "δ-Umgebung" von x0 , Symb.: Uδ(x0).
Bemerkung: Im R1 ist delta-Umgebung ein Intervall mit x0-δ <x< x0+δ.
Satz1: Mit jedem Pkt.x' der delta-Umg(x0) ist auch eine ganze delta-Umg(x') vollständig in delta(x0) enthalten, wenn δ' =δ -d(x',x0) ist.

Beweis: a sei beliebiger Pkt. in delta'(x'), dann ist d(a,x')<δ'
=> d(a,x0) ≤ d(x',x0) +d(a,x') <d(x',x0)+δ'
=> d(x',x0)+δ' = d(x',x0) +(δ-d(x',x0)) =δ
Definition Folgen im Rm:
Konvergenz:
{x(n)} sei Folge von Punkten x(n):
x(n) =( x(n)1, x(n)2,...x(n)m ) , dann heißt Folge {x(n)} konvergent, wenn es ein x*=(x(*)1, . . . , x(*)m ) mit einer beliebigen delta(x*)-Umg. gibt, so daß alle x(n) ab einem best.Index N>n innerhalb der delta(x*) liegen. (δ -Nδ' -Kriterium )
also: ∀n≥Nδ: d(x*,x(n) )<δ
Beschränktheit:
Eine Folge {x(n)} heißt beschränkt, wenn es ein k>0 gibt, so daß der Abstand zum Null-Pkt. ≤k ist, d(x((n),Null)≤k,∀n.
Fundamental-Folge:
Eine Folge {x(n)} heißt Fundamental-Folge, wenn gilt:
geg.δ>0 => ∃Nδ: d(x(n),x(k)) <δ , ∀n,k≥Nδ
Satz2: Ist {x(n)}->x* konvergent, dann gilt auch umgekehrt: {x(n)i}->x*i ,i=1,2,...,m
Wenn Folge konvergent, dann auch die Folgen der einzelnen Koordinaten und umgekehrt.
Zuerst ein paar Hilfssätze:

Nach Hilfsaussage2 gilt dann: d(x(n),x*)=Sum[j](d(x(n)j,x(*)j)) <c*sqrt(m) , bei c=δ/sqrt(m) ist d(x(n),x*) <δ ∀n≥max(N1,...,N(m)).
Also gilt auch: x(n)->x*.
Folgerung1: Der Limes einer konvergenten Folge im Rm ist eindeutig bestimmt, weil die Limes aus den j-ten Komponenten {x(n)j}->x(*)j eindeutig bestimmt sind.
Folgerung2: Eine konvergente Folge ist beschränkt, denn die d(x(n)j)≤k(j) sind beschränkt. Ist k=max(k(1),...,k(m)), so gilt auch:
d(x(n)j,Null) ≤k(j)) ≤k . Nach Hilfsaus.2 ist:
d(x(n)j,Null) ≤k*sqrt(m).
Folgerung3: Ist {x(n)} Fundamental-Folge, so ist {x(n)} ->konvergent.
3.11 Punkt-Mengen im Rm
Definition1 offene Mengen:
Eine Menge M heißt offen, wenn mit jedem Pkt. von M auch eine ganze delta-Umgebung zu M gehört.
Beispiele offener Mengen:
a) Jede delta-Umgebung ist nach Def. selbst offene Menge.
b) M= {x: a<x<b } ist Inter4vall im R1 und mit:
δ =1/2 *(b-a) , x0 =a+δ =>M={x}: d(x,x0)<delta; offene Menge.
c) M= {x=(x1,...,x(m)): a(i)<x(i)<b(i) ,i=1,...,m }
ist m-dim offenes Intervall. Für jede Projektion findet man ein δ(i) entspr. b), so daß gilt:
δ(i) =1/2 *(b(i)-a(i)) , x0 =a(i)+δ(i)
=> M={x(i): x0(i)-δ(i) <x(i)< x0(i)+δ(i) }
ist delta-Umgebung in der i-ten Koord.. Der Punkt x0=(x(0)1,...,x(0)m ) ist dann mit δ=min(δ(1),...,δ(m) ) Kern der Uδ(x0) -Umgebung, in der alle Punkte des m-dim offenes Intervall enthalten sind.
Definition2 Häufungspunkte:
Ein Pkt. x* heißt Häufungspunkt in der Menge M, wenn in jeder delta-Umg. von x* wenigstens ein weiterer Pkt. von M liegt.
Bemerkung: Nach dieser Def. braucht der Häufungspunkt x* nicht zur Menge M zu gehören: M:{x: a<x<b } => b ist Häufungspunkt von M. Anderseits gilt: Ist M offene Menge, so ist jeder Pkt. in M Häufungspunkt von M.
Satz1: Ist x* Häufungspunkt von M, dann gibt es eine Folge {x(n)} in M mit folg. Eigenschaften:
a) x(n)∈M b) x(n)≠x* c) {x(n)}->x*
Beweis: Wegen Häufungspunkt x* gilt für delta-Umg(x*) und δ=1/n , z.B. d(x(n),x*) <δ =1/n für n→∞ ist d(x(n),x*) <1/n , also Limes{d(x(n),x*)}=0
Satz2: x* Häufungspunkt in M, so gibt es in jeder delta-Umg(x*) unendl. viele weitere Punkte von M.
Beweis: Angenommen, es gibt nur endl. viele Punkte x1,...,x(k) , dann bilden wir:
δ(0) = min[d(x1,x*),...,d(x(k),x*) ] , dann liegt in der δ(0)-Umg(x*) kein weiterer Pkt. von M mehr. Dies ist aber Widerspruch zum Häufungspunkt x*.
Ende des Beweises
Folgerung: Gib es eine delta-Umgeb. zu einem Pkt.x aus M, in der kein weiterer Pkt. von M liegt, so heißt dieser Pkt.x isolierter Punkt in M.
Definition3 abgeschlossene Mengen:
Eine Menge M heißt abgeschlossen, wenn jeder Häufungspunkt von M zu M gehört.
Folgerung: M' sei Menge alle Häufungspunkte von M, dann ist die Vereinigungs-Menge mi M , M∪M' , abgeschlossen und heißt abgeschlossenen Hülle von M.
Definition4 Die Menge aller nicht zu M gehöriger Punkte heißt komplementär-Menge, Symb.: ⊂M
Beispiel:
M={x: d(x,x*)<1 }, dann ist:
⊂M ={x: d(x,x*)≥1 } (Komplementär(M))
Satz3:
M =offen, dann ⊂M abgeschlossen,
M =abgeschlossen, dann ⊂M offen.
Definition4 Kompakte Menge:
Eine Menge heißt beschränkt, wenn es ein k gibt, so daß d(x,Null)≤k ist, für alle x aus M.
Eine Menge heißt kompakt, wenn sie abgeschlossen und beschränkt ist.
Definition5 offene Überdeckung:
Ein Mengen-System Δ={M1,M2...} heißt offene Überdeckung von M, wenn gilt:
a) die Mengen M(j) ∈ Δ und offen
b) jeder Pkt. von M ist in wenigstens 1 Menge von Δ enthalten.
Satz4: zu offener Überdeck. v.kompakten Mengen (Satz von Heine-Borel)
M =kompakt, Δ =off.Überdeckung von M, dann genügen zur Überdeckung bereits endlich viele M(j) von Δ
(diese müssen sich nicht überlappen, tuen es aber, wenn die Elemente
dicht liegen)
Wenn man die delta-Umgeb. der Punkte in M nimmt, sind dies unendl. viele. Der Satz sagt nun aus, daß unendl. viele Punkte (nach δ-Kriterium) in einer Umgeb. liegen, mit einem endl.Abstand δ>0, so daß letzendlich endlich viele Umgebungen zur Überdeckung einer kompakten =beschränkten Punktmenge genügen.
Beweis: d(x,Null)≤k , ∀x∈M. Für die kompakte Menge M wird eine Normal-Unterteilung, durch Halbierung, vorgenommen. I0 sei M,
I1 =1-te Teilung =2m Teile, . . . ,
In =n-te Teilung =2n*m Teile , mit Kantenlängen k/2n*m Die n-Unterteilung wird solange fortgesetzt, bis alle In unter einer offenen Menge liegen. Sollten über einem der In-Teile immer noch unendl. viele offene Mengen liegen, so wird weiter geteilt. Dieser Prozeß ist aber endl. , da alle delta-Umgebungen ein δ >0 besitzen.
δ=min(M1δ,...,Mjδ,... ), n wird so groß gewählt, daß k/2n*m <δ ist. Damit habe ich eine endl.Auswahl aus Δ(M1,..) ausgewählt.
Ende des Beweises
Satz5:(Satz von Bolzano-Weierstraß )
Eine beschränkte Menge, die unendl. viele Punkte enthält, besitzt wenigstens einen Häufungspunkt.
Beweis indirekt: M besitze keinen Häufungspunkt, dann wäre M abgeschlossen und wegen Beschränktheit auch kompakt - und alle Punkte wären isoliert. Dann bilde ich zu allen Punkten, die u.U. auch isoliert sind, kleine δ-Umgeb., die keinen weiteren Punkt mehr enthalten.
Ergebnis: Man erhält eine off.Überdeckung von M mit unendl. vielen off. Mengen. Nach Satz4 (Heine-Borel) zuvor, genügen aber bereits endl. viele off. Mengen, damit jeder Pkt. in einer dieser {Mj} enthalten ist.
Das ist aber Widerspruch zur Voraussetzung =unendl. viele Elemente in M.
Ende des Beweises
Eine Menge M heißt offen, wenn mit jedem Pkt. von M auch eine ganze delta-Umgebung zu M gehört.
Beispiele offener Mengen:
a) Jede delta-Umgebung ist nach Def. selbst offene Menge.
b) M= {x: a<x<b } ist Inter4vall im R1 und mit:
δ =1/2 *(b-a) , x0 =a+δ =>M={x}: d(x,x0)<delta; offene Menge.
c) M= {x=(x1,...,x(m)): a(i)<x(i)<b(i) ,
ist m-dim offenes Intervall. Für jede Projektion findet man ein δ(i) entspr. b), so daß gilt:
δ(i) =1/2 *(b(i)-a(i)) , x0 =a(i)+δ(i)
=> M={x(i): x0(i)-δ(i) <x(i)< x0(i)+δ(i) }
ist delta-Umgebung in der i-ten Koord.. Der Punkt x0=(x(0)1,...,x(0)m ) ist dann mit δ=min(δ(1),...,δ(m) ) Kern der Uδ(x0) -Umgebung, in der alle Punkte des m-dim offenes Intervall enthalten sind.
Definition2 Häufungspunkte:
Ein Pkt. x* heißt Häufungspunkt in der Menge M, wenn in jeder delta-Umg. von x* wenigstens ein weiterer Pkt. von M liegt.
Bemerkung: Nach dieser Def. braucht der Häufungspunkt x* nicht zur Menge M zu gehören: M:{x: a<x<b } => b ist Häufungspunkt von M. Anderseits gilt: Ist M offene Menge, so ist jeder Pkt. in M Häufungspunkt von M.
Satz1: Ist x* Häufungspunkt von M, dann gibt es eine Folge {x(n)} in M mit folg. Eigenschaften:
a) x(n)∈M b) x(n)≠x* c) {x(n)}->x*
Beweis: Wegen Häufungspunkt x* gilt für delta-Umg(x*) und δ=1/n , z.B. d(x(n),x*) <δ =1/n für n→∞ ist d(x(n),x*) <1/n , also Limes{d(x(n),x*)}=0
Satz2: x* Häufungspunkt in M, so gibt es in jeder delta-Umg(x*) unendl. viele weitere Punkte von M.
Beweis: Angenommen, es gibt nur endl. viele Punkte x1,...,x(k) , dann bilden wir:
δ(0) = min[d(x1,x*),...,d(x(k),x*) ] , dann liegt in der δ(0)-Umg(x*) kein weiterer Pkt. von M mehr. Dies ist aber Widerspruch zum Häufungspunkt x*.
Folgerung: Gib es eine delta-Umgeb. zu einem Pkt.x aus M, in der kein weiterer Pkt. von M liegt, so heißt dieser Pkt.x isolierter Punkt in M.
Definition3 abgeschlossene Mengen:
Eine Menge M heißt abgeschlossen, wenn jeder Häufungspunkt von M zu M gehört.
Folgerung: M' sei Menge alle Häufungspunkte von M, dann ist die Vereinigungs-Menge mi M , M∪M' , abgeschlossen und heißt abgeschlossenen Hülle von M.
Definition4 Die Menge aller nicht zu M gehöriger Punkte heißt komplementär-Menge, Symb.: ⊂M
Beispiel:
M={x: d(x,x*)<1 }, dann ist:
⊂M ={x: d(x,x*)≥1 } (Komplementär(M))
Satz3:
M =offen, dann ⊂M abgeschlossen,
M =abgeschlossen, dann ⊂M offen.
Definition4 Kompakte Menge:
Eine Menge heißt beschränkt, wenn es ein k gibt, so daß d(x,Null)≤k ist, für alle x aus M.
Eine Menge heißt kompakt, wenn sie abgeschlossen und beschränkt ist.
Definition5 offene Überdeckung:
Ein Mengen-System Δ={M1,M2...} heißt offene Überdeckung von M, wenn gilt:
a) die Mengen M(j) ∈ Δ und offen
b) jeder Pkt. von M ist in wenigstens 1 Menge von Δ enthalten.
Satz4:
M =kompakt, Δ =off.Überdeckung von M, dann genügen zur Überdeckung bereits endlich viele M(j) von Δ
Wenn man die delta-Umgeb. der Punkte in M nimmt, sind dies unendl. viele. Der Satz sagt nun aus, daß unendl. viele Punkte (nach δ-Kriterium) in einer Umgeb. liegen, mit einem endl.Abstand δ>0, so daß letzendlich endlich viele Umgebungen zur Überdeckung einer kompakten =beschränkten Punktmenge genügen.
Beweis: d(x,Null)≤k , ∀x∈M. Für die kompakte Menge M wird eine Normal-Unterteilung, durch Halbierung, vorgenommen. I0 sei M,
I1 =1-te Teilung =2m Teile, . . . ,
In =n-te Teilung =2n*m Teile , mit Kantenlängen k/2n*m Die n-Unterteilung wird solange fortgesetzt, bis alle In unter einer offenen Menge liegen. Sollten über einem der In-Teile immer noch unendl. viele offene Mengen liegen, so wird weiter geteilt. Dieser Prozeß ist aber endl. , da alle delta-Umgebungen ein δ >0 besitzen.
δ=min(M1δ,...,Mjδ,... ), n wird so groß gewählt, daß k/2n*m <δ ist. Damit habe ich eine endl.Auswahl aus Δ(M1,..) ausgewählt.
Satz5:
Eine beschränkte Menge, die unendl. viele Punkte enthält, besitzt wenigstens einen Häufungspunkt.
Beweis indirekt: M besitze keinen Häufungspunkt, dann wäre M abgeschlossen und wegen Beschränktheit auch kompakt - und alle Punkte wären isoliert. Dann bilde ich zu allen Punkten, die u.U. auch isoliert sind, kleine δ-Umgeb., die keinen weiteren Punkt mehr enthalten.
Ergebnis: Man erhält eine off.Überdeckung von M mit unendl. vielen off. Mengen. Nach Satz4 (Heine-Borel) zuvor, genügen aber bereits endl. viele off. Mengen, damit jeder Pkt. in einer dieser {Mj} enthalten ist.
Das ist aber Widerspruch zur Voraussetzung =unendl. viele Elemente in M.
3.12 Zusammenfassung und Ausblick:
Mit den Reellen Zahlen hat man einen vollständigen Raum, in dem alle
elementaren Verknüpfungen Add./Mult./Potenz zugelassen sind, samt Umkehroperationen.
Für die Erweiterung zum Rm , m>1 haben wir bis jetzt nur 3 Verküpf. def.:
- Linearkombinationen L()
- Skalarprodukt(x,y)
- Norm(x) ,Abstand x zu Null
Damit hat der m-dim Eukl. Raum die Eigenschaften eines linearen- ,normierten-, metrischen Raumes mit Skalarprodukt.
Zusätzlich kann man durch die Abstands-Norm die Verb.Linie (Null->x) als gerichtete Line von Null nach x interpretieren, welche dann die Länge =Norm(x) hat.
Dadurch wird die Punkt-Menge {x: (x1,...,x(m) } zu einem Zentral-Richtungs-Feld mit Zentrum Null äquivalent. In Verbindung mit L() erhält man dann eine spez. Richtung-Verknüpfungs-Axiomatik:
Bild , Reell-8.jpg
In der Folge wird eine zusätzlich multiplikative- Verknüpfung zum Skalarprodukt definiert, nämlich das sogenannte "Volumen-Produkt" von mehreren Punkten (Richtungen): V(p1,...,P(m)) =(p1*p2*..*p(m)) , dessen Betrag optisch mit dem, von den p1,p2,..,p((m) -Richtungen aufgespannten Volumen übereinstimmt, hier, im Bild, mit der Fläche des Parallelogramms.
Entsprechend der Methode: Triangulation /Rasterung der Ebene, wie in der Abhandlung "1. Euklid.-Geometrie" Abschnitt 1.6 beschrieben, kann eine Menge von mind. m Richtungen {p1,...,p(m)} zur Rasterung des Rm herangezogen werden. Über L(p1,...,p(m)) werden Pfade von Element zu Element im Rm konstruiert. Damit ist es möglich, geometr. Objekte und sonst. Punktmengen im Rm zu positionieren und mit zulässigen Operationen (Verknüpfungen) im Raum zu transformieren.
Diese logisch nächsten Schritte sind Basis der Untersuchungen in der Analytische Geometrie I und den darauf aufbauenden Zweigen der Mathematik: Analysis, Infinitesimal- Rechnung, etc.
->Anfang
Für die Erweiterung zum Rm , m>1 haben wir bis jetzt nur 3 Verküpf. def.:
- Linearkombinationen L()
- Skalarprodukt(x,y)
- Norm(x) ,Abstand x zu Null
Damit hat der m-dim Eukl. Raum die Eigenschaften eines linearen- ,normierten-, metrischen Raumes mit Skalarprodukt.
Zusätzlich kann man durch die Abstands-Norm die Verb.Linie (Null->x) als gerichtete Line von Null nach x interpretieren, welche dann die Länge =Norm(x) hat.
Dadurch wird die Punkt-Menge {x: (x1,...,x(m) } zu einem Zentral-Richtungs-Feld mit Zentrum Null äquivalent. In Verbindung mit L() erhält man dann eine spez. Richtung-Verknüpfungs-Axiomatik:

In der Folge wird eine zusätzlich multiplikative- Verknüpfung zum Skalarprodukt definiert, nämlich das sogenannte "Volumen-Produkt" von mehreren Punkten (Richtungen): V(p1,...,P(m)) =(p1*p2*..*p(m)) , dessen Betrag optisch mit dem, von den p1,p2,..,p((m) -Richtungen aufgespannten Volumen übereinstimmt, hier, im Bild, mit der Fläche des Parallelogramms.
Entsprechend der Methode: Triangulation /Rasterung der Ebene, wie in der Abhandlung "1. Euklid.-Geometrie" Abschnitt 1.6 beschrieben, kann eine Menge von mind. m Richtungen {p1,...,p(m)} zur Rasterung des Rm herangezogen werden. Über L(p1,...,p(m)) werden Pfade von Element zu Element im Rm konstruiert. Damit ist es möglich, geometr. Objekte und sonst. Punktmengen im Rm zu positionieren und mit zulässigen Operationen (Verknüpfungen) im Raum zu transformieren.
Diese logisch nächsten Schritte sind Basis der Untersuchungen in der Analytische Geometrie I und den darauf aufbauenden Zweigen der Mathematik: Analysis, Infinitesimal- Rechnung, etc.
Weitere Betrachtungen:
Euklidische Geometrie ,
Modell der reellen Zahlen ,
analytische Geometrie I ,
analytische Geometrie II ,
Euklidischer Raum ,
Analysis 1, Abbildungen ,
kleinere Beispiele der Himmelsmechanik im Newton-Modell ,
Bewegungen im Newton-Raum ,