| 0. Einflußfaktoren auf das Temperatur-Niveau |
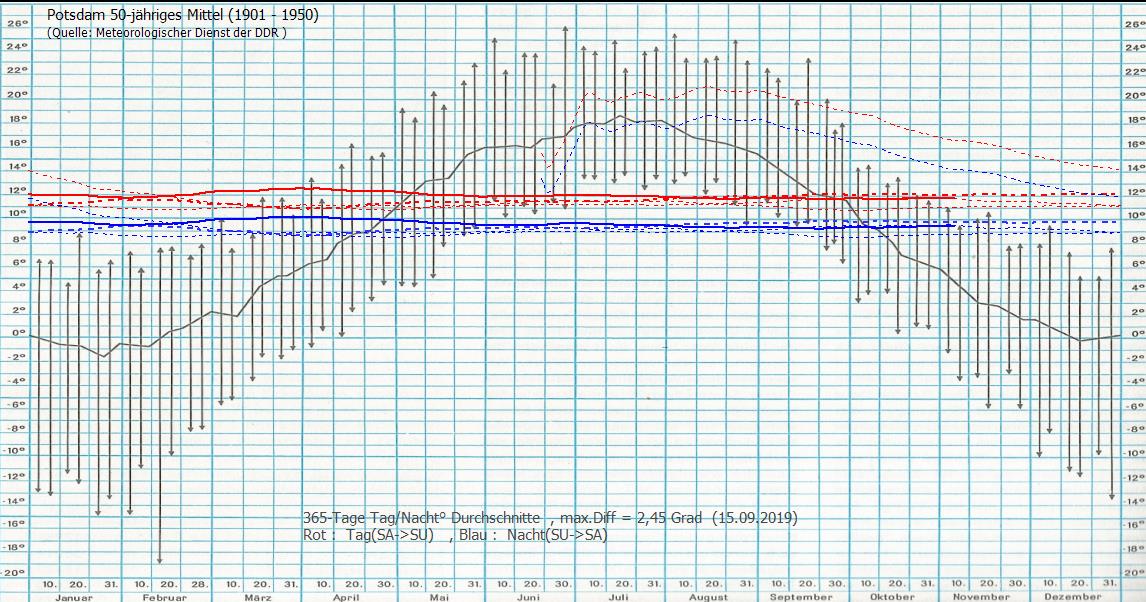
Temp.Messungen rueckwaerts fuer die Durchschnitts-Bildung herangezogen! (48 Messungen / Tag)
Der Jahresdurchschnitt zwischen Tag-/Nacht-Temperaturen bildet das Temp_Niveau ,hier 10°, für die beobachtete Umgebung, Behringen (Thür.Becken). Er gleicht alle Jahres -zeitlichen Schwankungen aus und ist nur noch abhängig von der Wechselwirkung Erde<->Sonne und Erde<->Mond.
Die rot/blaue-Temperatur-Linie verlaeuft waagerecht , steigend oder fallend :
waagerecht: Klima_stabil!
steigend: Klima_Erwaermung!
fallend: Klima_Erkaeltung!
Siehe auch: Vergleich mit der anderen lokalen Umgebung:
Math.Grundlagen
zurück
0.1 Wechselwirkung Erde mit Mond und Sonne
Unter Wechselwirkungen im physikalischen Sinn (Newton-Raum) kommen in der
Hauptsache die Gravitation-(Sonne/Mond), die Strahlungs-Emission-Sonne sowie im
geringen Maße die Eigenwärme der Erde in Frage.
Gravitation, das sind die Gezeitenkräfte, die auf die Erdoberfläche wirken, und zu Reibungswärme führen.
Eigenwärme, sie kommt aus dem Erdinneren (Vulkane, Erdbeben, etc.) und ist ebenfalls Teil des aktuellen Temperatur-Niveaus.
Sonnenenergie, sie besteht aus Elektromagnetischer Strahlung (Null-Masse mit c=Lichtgeschwindigkeit) und Strahlung geladener Teilchen (kleiner c, je mehr Masse, desto langsamer). Das Besondere hierbei ist, dass sie nur in der halben Zeit wirkt, also tagsüber, und in der Nacht vorbei strahlt. So entsteht der relativ stabile Unterschied zwischen Tag- und Nacht-Temperaturen, in der Grafik hier ca. 2,5°, über ein ganzes Jahr verteilt. Umgangs-sprachlich sagt man: "Nachts kühlt es aus, Tagsüber erwärmt es sich wieder". Betrachtet man es aber im Newton-Raum, so wird am Tage Energie zugeführt und in der Nacht nicht. Dies dürfte nach Energie-Erhaltungs-Satz nicht zum Sinken der Nacht-Temperaturen führen, es sei denn, es gibt eine ständige Energie-Abstrahlung von der Erde, sowohl nachts, als auch am Tage!
Die Energie-Abstrahlung ist es also, die für die Tag- Nacht- Temperatur Unterschiede verantwortlich ist. Die °Diff. hier 2,5°, kann man somit als Maß für die Abstrahlung sehen:
Temp-Diff: Maß für die Abstrahlung.
Temp-Niveau: Maß für Das Gleichgewicht zwischen Energiezufuhr und -Abstrahlung.
Beispielsweise haben die Sonnen-fernen Planeten ein wesentlich geringeres Temp-Niveau an der Oberfläche bei gleicher Abstrahlung, aber deutlich geringerer Energie-Zufuhr von Sonne.
Klima-Erwärmung: Bei gleichbleibender Sonnen-Energie-Emmission bleibt für eine Erhöhung des Temp-Niveaus (Klima-Erwärmung) als Ursache nur eine Verringerung des Maßes für die Abstrahlung übrig, evtl. durch Bremswirkung der Lufthülle.
Im beobachtbaren Raum, Newton-Raum, wird für die Grav.- und Stahlungs-Wirkung ein kugelförmiges Zentralfeld, mit Punkt-Quelle (z.B. Sonnen-Schwerpkt.), angenommen, dessen Wirkung mit dem Quadrat des Abstandes von der Quelle abnimmt. Bei den folg. Betrachtungen gehen wir immer von homogenen Feldern aus, die es aber in Wirklichkeit nicht gibt!
Gravitation, das sind die Gezeitenkräfte, die auf die Erdoberfläche wirken, und zu Reibungswärme führen.
Eigenwärme, sie kommt aus dem Erdinneren (Vulkane, Erdbeben, etc.) und ist ebenfalls Teil des aktuellen Temperatur-Niveaus.
Sonnenenergie, sie besteht aus Elektromagnetischer Strahlung (Null-Masse mit c=Lichtgeschwindigkeit) und Strahlung geladener Teilchen (kleiner c, je mehr Masse, desto langsamer). Das Besondere hierbei ist, dass sie nur in der halben Zeit wirkt, also tagsüber, und in der Nacht vorbei strahlt. So entsteht der relativ stabile Unterschied zwischen Tag- und Nacht-Temperaturen, in der Grafik hier ca. 2,5°, über ein ganzes Jahr verteilt. Umgangs-sprachlich sagt man: "Nachts kühlt es aus, Tagsüber erwärmt es sich wieder". Betrachtet man es aber im Newton-Raum, so wird am Tage Energie zugeführt und in der Nacht nicht. Dies dürfte nach Energie-Erhaltungs-Satz nicht zum Sinken der Nacht-Temperaturen führen, es sei denn, es gibt eine ständige Energie-Abstrahlung von der Erde, sowohl nachts, als auch am Tage!
Die Energie-Abstrahlung ist es also, die für die Tag- Nacht- Temperatur Unterschiede verantwortlich ist. Die °Diff. hier 2,5°, kann man somit als Maß für die Abstrahlung sehen:
Temp-Diff: Maß für die Abstrahlung.
Temp-Niveau: Maß für Das Gleichgewicht zwischen Energiezufuhr und -Abstrahlung.
Beispielsweise haben die Sonnen-fernen Planeten ein wesentlich geringeres Temp-Niveau an der Oberfläche bei gleicher Abstrahlung, aber deutlich geringerer Energie-Zufuhr von Sonne.
Klima-Erwärmung: Bei gleichbleibender Sonnen-Energie-Emmission bleibt für eine Erhöhung des Temp-Niveaus (Klima-Erwärmung) als Ursache nur eine Verringerung des Maßes für die Abstrahlung übrig, evtl. durch Bremswirkung der Lufthülle.
Im beobachtbaren Raum, Newton-Raum, wird für die Grav.- und Stahlungs-Wirkung ein kugelförmiges Zentralfeld, mit Punkt-Quelle (z.B. Sonnen-Schwerpkt.), angenommen, dessen Wirkung mit dem Quadrat des Abstandes von der Quelle abnimmt. Bei den folg. Betrachtungen gehen wir immer von homogenen Feldern aus, die es aber in Wirklichkeit nicht gibt!

Ein Teil der Strahlung E2 wird reflektiert, der Rest beeinflußt das Temp-Niveau auf der Erdoberfläche.
0.2 Zentralfeld Sonne
Die am Himmel zu beobachtenden Phänomenen wurden ab Mittelalter zunehmend wissenschaftlich
untersucht, Tycho Brahe /Kopernicus etc., und in Verbindung mit Entwicklung der Mathematik
, über die Stationen:
Eukl.Geometrie ,
analytische Gemetrie und
Eukl.Raum
(Menge aller m-Tupel reeller Zahlen), durch Isaac Newton zu einem Modell des
lokalen Raumes (Newton-Raum) entwickelt, in welchen alle Beobachtungen
mit wenigen Axiomen beschrieben und berechnet werden konnten/ können.
Kernstück des Modells ist die Grav.Theorie und die Theorie der Relativ-Bewegungen von Körpern (gleichförmig o. Kräfte-beeinflusst). Dabei steht das Prinzip, die Wechselwirkungen zwischen Körpern durch Wechselwirkungen ihrer Schwerpunkte zu ersetzen (Punktmasse), den Beobachtungen nicht im Weg.
Die Verbindung des Newton-Raum mit dem 3-dim.Eukl.Raum als Prinzip ermöglichte es, den Körpern Koord. zu geben in Bezug auf einen (relativen) Null-Punkt, z.B. Beobachtungs - Zentrum.
Dieses Prinzip hat aber seine Grenzen im Unendlichen und Null. Z.B. wäre es im Newton-Raum unmöglich, sich einer Pkt-Masse bis zum Abstand Null zu nähern, im Eukl.Raum aber möglich, weil dann die Grav.Kräfte ->unendlich wachsen würden. Ausserdem haben in der Realität Körper(=Masse) endl. Ausdehnung und endliches Grav.Feld.
Auf das Universum bezogen müssten alle Masse-Punkte isoliert liegen, endl.Abstand voneinander haben und keine Häufungs-Punkte (im math. Sinn) bilden, um keine unendlich große lokale Ansammlungen darzustellen.
Seit Einstein wissen wir, dass das beobachtbare Universum von der (endl.) Lichtgeschwindigkeit bestimmt wird und somit tatsächlich endlich ist, einschließlich der Wechselwirkungen: Gravitation und Stahlung.
Eine weitere Einschränkung des Newton-Modells gibt es bei den zu beobachtenden Dreh -bewegungen von Galaxien
Neuerdings haben die Fragen nach der Gültigkeit der klass. Physik in Grenzbereichen an Bedeutung gewonnen, wie z.B.: "Wie weit kann man sich einer Pkt.Masse nähern, damit es zu keinen Unendlich -keiten kommt, Masse, Kräfte, Geschwind.?"
Interessant sind diese Fragestellungen auch im Zusammenhang mit der Untersuchung der Existenz von schwarzen Löchern.
Kernstück des Modells ist die Grav.Theorie und die Theorie der Relativ-Bewegungen von Körpern (gleichförmig o. Kräfte-beeinflusst). Dabei steht das Prinzip, die Wechselwirkungen zwischen Körpern durch Wechselwirkungen ihrer Schwerpunkte zu ersetzen (Punktmasse), den Beobachtungen nicht im Weg.
Die Verbindung des Newton-Raum mit dem 3-dim.Eukl.Raum als Prinzip ermöglichte es, den Körpern Koord. zu geben in Bezug auf einen (relativen) Null-Punkt, z.B. Beobachtungs - Zentrum.
Dieses Prinzip hat aber seine Grenzen im Unendlichen und Null. Z.B. wäre es im Newton-Raum unmöglich, sich einer Pkt-Masse bis zum Abstand Null zu nähern, im Eukl.Raum aber möglich, weil dann die Grav.Kräfte ->unendlich wachsen würden. Ausserdem haben in der Realität Körper(=Masse) endl. Ausdehnung und endliches Grav.Feld.
Auf das Universum bezogen müssten alle Masse-Punkte isoliert liegen, endl.Abstand voneinander haben und keine Häufungs-Punkte (im math. Sinn) bilden, um keine unendlich große lokale Ansammlungen darzustellen.
Seit Einstein wissen wir, dass das beobachtbare Universum von der (endl.) Lichtgeschwindigkeit bestimmt wird und somit tatsächlich endlich ist, einschließlich der Wechselwirkungen: Gravitation und Stahlung.
Eine weitere Einschränkung des Newton-Modells gibt es bei den zu beobachtenden Dreh -bewegungen von Galaxien
Neuerdings haben die Fragen nach der Gültigkeit der klass. Physik in Grenzbereichen an Bedeutung gewonnen, wie z.B.: "Wie weit kann man sich einer Pkt.Masse nähern, damit es zu keinen Unendlich -keiten kommt, Masse, Kräfte, Geschwind.?"
Interessant sind diese Fragestellungen auch im Zusammenhang mit der Untersuchung der Existenz von schwarzen Löchern.
0.3 Beobachtungs-Raum im Universum:
Bild 3 , Univers1.jpg
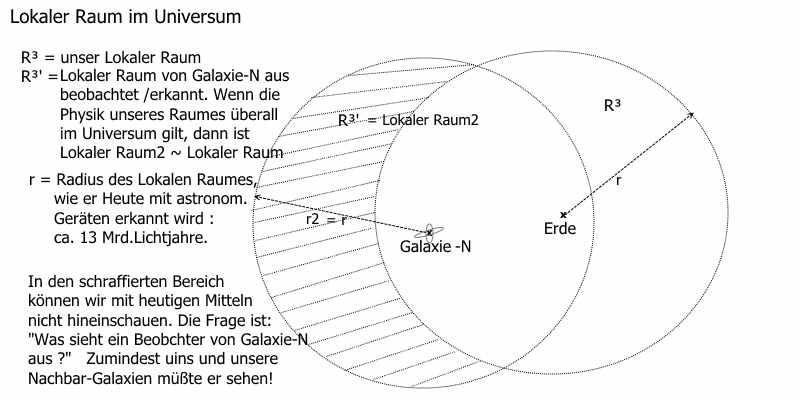
Bild 3 , Univers1.jpg

R³ und R³' sind, wie zuvor ausgeführt, Newton-Raum und zugleich Einstein-Raum. Für Umgebungen U kleiner Galaxien-Grösse (z.B. Sonnen -System) kann man bei Beobachtungen sicher die Newtonsche-Axiomatik anwenden. Für Übergänge von einer Umgebung zu einer Anderen muß man aber die Einstein- Transformationen berücksichtigen.
1.0 Durchschnitts-Berechnungen im Newton-/Euklid.-Raum:
Ausgangspunkt:
Elemente im Newton-Raum (Objekte, Ereignisse, Wirkungen etc.), denen eine Ort-Eigenschaft zugeordnet werden kann, stehen ueber dem Abstands-Begriff in einer Wechselwirkung zueinander.
Durch die Aequivalenz des Newton-Raumes zum Eukl.Raum (Ort= (x,y,z)),werden den Elementen im phys. Raum -> Punkte oder Punkt-Mengen des Eukl.Raumes zugewiesen.
Hinweis: Zu Beachten ist, dass es im phys.Raum keine Ausdehnung "Null" oder "unendlich" gibt. D.h. z.B., eine Masse hat im Newton-Raum also immer eine Ausdehnung >0 (=Volumen), waehrend im Eukl.Raum dem Massen-Mittelpkt. ein Ort = Punkt zugewiesen wird, so dass mit einer gewichteten Punkt-Masse gerechnet werden kann, wie folgt: m*p1 (m= Masse , p1= Ort).
Durch dieses Prinzip der Ersetzung der Ort-Eigenschaft eines Elementes durch seinen Mittelpunkt, kann man folg. Aussagen treffen:
1. Haben 2 Mittelpunkte einen Abstand>0, so sind z.B. auch die zugehörigen Massen verschieden.
2. Zwischen 2 verschiedenen Punkten (Abstand>0) passt immer auch eine ganze δ-Umgebung zu den Punkten dazwischen. Diese Tatsache garantiert, das die zu den Mittelpunkten gehörigen phys.Elementen (Objekte, Massen, Ereignisse ...) eine Ausdehnung>0 haben.
3. Mehrere Elemente koennen wegen der Abstaende>0 vermittelt oder ausgeglichen werden.
(p1-p2) und (p1+p2) sind 2 Richtungen im Eukl.Raumes, die sich jeweils in der Mitte in einem Pkt. x schneiden. Beide Richtungen legen in ihren Endpunkten ein Parallelogramm PG fest:
PG =(0, p1, p1+p2, p2). Der Punkt x teilt also die Richtungen (p1-p2) u. (p1+p2) genau in der Mitte, so dass gilt:
Bild , Temp-niv0.jpg
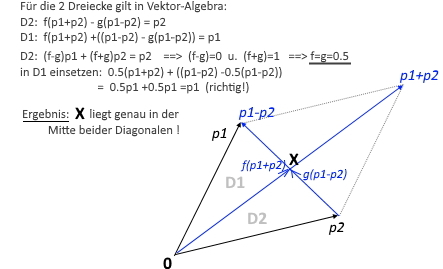
(p1-x) = (x-p2), = allg. Gleichgewichts-Prinzip
Jetzt kann man diesen Sachverhalt verschieden interpretieren:
- x ist Mittel- o.Schwerpunkt der Strecke (p1p2)
- x ist Mittel- o.Schwerpunkt des PG=(0,p1,p1+p2,p2)
In der Umformung: 1*(p1-x) + 1*(p2-x) = Null drueckt das Gleichgewichts-Prinzip die Beziehung zweier statischer Momente, die in einem Punkt angreifen, wie folgt aus:
Ergibt die Summe der Momente 1*(p1-x) und 1*(p2-x) den Null-Vektor/Richtung, dann stehen sie im Gleichgewicht zueinander.
Vorbemerkungen:(über Elemente im abstrakten Raum R)
Der abstrakte Raum ist zunächst "leer", "neutral", "eigenschaftslos", also, man weiß anfangs nichts über ihn.
Spricht man von einem Element E in R, symb.: E∈R, so erhält man "Erkenntnis-theoretisch" einen Unterschied oder Differenz im Raum, nämlich das Element im Unterschied zum Rest des Raumes. Man kann also beide voneinander unterscheiden (Erkennen). Ob es sich bei einem Element um einen Körper, Materie, Emission, Ereignis, Wechselwirkung etc. handelt, spielt nach Erkenntnis-Theorie im abstrakten Raum zunächst einmal keine Rolle. Erst im fortgeschrittenen wissenschaftl. Erkenntnis-Prozess werden die Elemente mit entspr. Ereignissen u. Eigenschaften, wie Temp., Masse, Orte, Gravitation, Geschwindigkeiten, Kräfte etc., assoziiert.
Relationen und Gleichgewicht: Der abstrakte Raum ist ohne erkennbare Unterschiede, Differenzen, Elemente neutral oder in sich betrachtet "im Gleichgewicht", also in einem nicht unterscheidbarem, gleichmäßigem (gleichgewichtetem) Zustand, nämlich "Null". Der Zustand Null ist eine Kategorie in der Erkenntnis-Theorie, die nicht Eigenschaften der Elemente beschreibt, sondern den Gleichgewichts-Zustand des abstrakten Raumes bezeichnet.
Durch die Diff.-Bildung eines Elementes mit sich selbst wird der Gleichgewichts-Zustand von R wiederhergestellt oder zum Ausdruck gebracht. Symb.: E-E=0 .Ein einzelnes Element drückt dagegen ein Ungleichgewicht in R aus: E≠0
Element-Folgen und Null-Summen-Differenzen: Zwischen eine Element-Diff. E-E=0 können weitere Element-Diff. eingefügt werden wie folgt: E-E1 +E1-E2 +E2- .... -E =0
Allg.: Sum(Ej-Ej-1) -(En-E0) =0 ,j=1...,n
z.B. n=3: (E1 -E0) +(E2 -E1) +(E3 -E2)
-(E3 -E0) =0
Da jedes Element Lin.Komb() anderer Elemente in R ist kann ein beliebiges Element auch in der allg.Form: a*E, f=reell/kompl. Multiplikator dargestellt werden.
Allgemein erhält man für mehrere Elemente eine sogenannte "gewichtete Element-Folge": {aj*Ej} mit zugehöriger Null-Summen-Differenz:
(1) Sum(aj*Ej -aj-1*Ej-1) -(an*En -a0*E0) =0
Gleichung (1) ensteht dadurch, daß zwei gleiche Element-Folgen, als Lin.Komb() betrachtet, paarweise voneinander abgezogen werden mit um "1" verschobenem Index:
(1a) {aj*Ej} ,j=0,1...,n
(1b) {aj*Ej} ,j=0,1...,n
=> Sum(aj*Ej) -Sum(aj*Ej) =0
Wenn man in Folge (1b) die Elemente Ej als "gleich" betrachtet und Ej=X setzt, formt sich die Null-Summen-Differenz wie folgt um :
(1) Sum(aj*Ej -ajX) =0 ,j=1...,n ; nach X auflösen:
=> Sum(aj*Ej) = Sum(aj) *X
=> Sum(aj*Ej) /Sum(aj) = X ,j=1...,n
Das Problem von Durchschnitts-Berechnungen wird, wegen des Bezuges auf vorliegende Wetter-App: "wetter-reimann.de", an Hand vom Temperatur-Messungen untersucht, welche dazu mit einer Folge von Elementen des Eukl.Raumes assoziiert werden. Beliebige physikalische Messreihen können so abstrakt mit math.Methoden (z.B. statistisch) bewertet werden.
Elemente im Newton-Raum (Objekte, Ereignisse, Wirkungen etc.), denen eine Ort-Eigenschaft zugeordnet werden kann, stehen ueber dem Abstands-Begriff in einer Wechselwirkung zueinander.
Durch die Aequivalenz des Newton-Raumes zum Eukl.Raum (Ort= (x,y,z)),werden den Elementen im phys. Raum -> Punkte oder Punkt-Mengen des Eukl.Raumes zugewiesen.
Hinweis: Zu Beachten ist, dass es im phys.Raum keine Ausdehnung "Null" oder "unendlich" gibt. D.h. z.B., eine Masse hat im Newton-Raum also immer eine Ausdehnung >0 (=Volumen), waehrend im Eukl.Raum dem Massen-Mittelpkt. ein Ort = Punkt zugewiesen wird, so dass mit einer gewichteten Punkt-Masse gerechnet werden kann, wie folgt: m*p1 (m= Masse , p1= Ort).
Durch dieses Prinzip der Ersetzung der Ort-Eigenschaft eines Elementes durch seinen Mittelpunkt, kann man folg. Aussagen treffen:
1. Haben 2 Mittelpunkte einen Abstand>0, so sind z.B. auch die zugehörigen Massen verschieden.
2. Zwischen 2 verschiedenen Punkten (Abstand>0) passt immer auch eine ganze δ-Umgebung zu den Punkten dazwischen. Diese Tatsache garantiert, das die zu den Mittelpunkten gehörigen phys.Elementen (Objekte, Massen, Ereignisse ...) eine Ausdehnung>0 haben.
3. Mehrere Elemente koennen wegen der Abstaende>0 vermittelt oder ausgeglichen werden.
(p1-p2) und (p1+p2) sind 2 Richtungen im Eukl.Raumes, die sich jeweils in der Mitte in einem Pkt. x schneiden. Beide Richtungen legen in ihren Endpunkten ein Parallelogramm PG fest:
PG =(0, p1, p1+p2, p2). Der Punkt x teilt also die Richtungen (p1-p2) u. (p1+p2) genau in der Mitte, so dass gilt:

(p1-x) = (x-p2)
Jetzt kann man diesen Sachverhalt verschieden interpretieren:
- x ist Mittel- o.Schwerpunkt der Strecke (p1p2)
- x ist Mittel- o.Schwerpunkt des PG=(0,p1,p1+p2,p2)
In der Umformung: 1*(p1-x) + 1*(p2-x) = Null drueckt das Gleichgewichts-Prinzip die Beziehung zweier statischer Momente, die in einem Punkt angreifen, wie folgt aus:
Ergibt die Summe der Momente 1*(p1-x) und 1*(p2-x) den Null-Vektor/Richtung, dann stehen sie im Gleichgewicht zueinander.
Vorbemerkungen:
Der abstrakte Raum ist zunächst "leer", "neutral", "eigenschaftslos", also, man weiß anfangs nichts über ihn.
Spricht man von einem Element E in R, symb.: E∈R, so erhält man "Erkenntnis-theoretisch" einen Unterschied oder Differenz im Raum, nämlich das Element im Unterschied zum Rest des Raumes. Man kann also beide voneinander unterscheiden (Erkennen). Ob es sich bei einem Element um einen Körper, Materie, Emission, Ereignis, Wechselwirkung etc. handelt, spielt nach Erkenntnis-Theorie im abstrakten Raum zunächst einmal keine Rolle. Erst im fortgeschrittenen wissenschaftl. Erkenntnis-Prozess werden die Elemente mit entspr. Ereignissen u. Eigenschaften, wie Temp., Masse, Orte, Gravitation, Geschwindigkeiten, Kräfte etc., assoziiert.
Relationen und Gleichgewicht: Der abstrakte Raum ist ohne erkennbare Unterschiede, Differenzen, Elemente neutral oder in sich betrachtet "im Gleichgewicht", also in einem nicht unterscheidbarem, gleichmäßigem (gleichgewichtetem) Zustand, nämlich "Null". Der Zustand Null ist eine Kategorie in der Erkenntnis-Theorie, die nicht Eigenschaften der Elemente beschreibt, sondern den Gleichgewichts-Zustand des abstrakten Raumes bezeichnet.
Durch die Diff.-Bildung eines Elementes mit sich selbst wird der Gleichgewichts-Zustand von R wiederhergestellt oder zum Ausdruck gebracht. Symb.: E-E=0 .Ein einzelnes Element drückt dagegen ein Ungleichgewicht in R aus: E≠0
Element-Folgen und Null-Summen-Differenzen: Zwischen eine Element-Diff. E-E=0 können weitere Element-Diff. eingefügt werden wie folgt: E-E1 +E1-E2 +E2- .... -E =0
Allg.: Sum(Ej-Ej-1) -(En-E0) =0 ,
Da jedes Element Lin.Komb() anderer Elemente in R ist kann ein beliebiges Element auch in der allg.Form: a*E, f=reell/kompl. Multiplikator dargestellt werden.
Allgemein erhält man für mehrere Elemente eine sogenannte "gewichtete Element-Folge": {aj*Ej} mit zugehöriger Null-Summen-Differenz:
(1) Sum(aj*Ej -aj-1*Ej-1) -(an*En -a0*E0) =0
Gleichung (1) ensteht dadurch, daß zwei gleiche Element-Folgen, als Lin.Komb() betrachtet, paarweise voneinander abgezogen werden mit um "1" verschobenem Index:
(1a) {aj*Ej} ,
(1b) {aj*Ej} ,
=> Sum(aj*Ej) -Sum(aj*Ej) =0
Wenn man in Folge (1b) die Elemente Ej als "gleich" betrachtet und Ej=X setzt, formt sich die Null-Summen-Differenz wie folgt um :
(1) Sum(aj*Ej -ajX) =0 ,
=> Sum(aj*Ej) = Sum(aj) *X
=> Sum(aj*Ej) /Sum(aj) = X ,
Das Problem von Durchschnitts-Berechnungen wird, wegen des Bezuges auf vorliegende Wetter-App: "wetter-reimann.de", an Hand vom Temperatur-Messungen untersucht, welche dazu mit einer Folge von Elementen des Eukl.Raumes assoziiert werden. Beliebige physikalische Messreihen können so abstrakt mit math.Methoden (z.B. statistisch) bewertet werden.
1.1 Mittelpunkts-, Schwerpunkts-, Gleichgewichts- Berechnungen:
Assoziierung von Objekt-Eigenschaften:
Bei der Assoziierung von Objekt-Eigenschaften geht es darum, gleiche Eigenschaften, die in Messreihen vorliegen (bei uns Temp.-Messungen), in spez. Element-Folgen des Eukl.Raumes zu ueberfuehren.
M={fi*pi)} sei eine solche spezielle Elementfolge. Diese Form ist keine Einschränkung der Allgemeinheit, da jede Folge {pi)} auch gleichzeitig spez.Folge: {1*pi)} ist.(fi =reelle Zahlen, pi =Pkte. des Rm )
Begriffsbildung und Sachverhalt:
Bei den Begriffen: Mittel-, Gleichgewichts-, Schwer-punkt etc. handelt es sich im Allgemeinen immer um den gleichen Sachverhalt, nämlich:
Berechnung des gewichteten Mittels einer Folge M={fi*pi} .
Dieses gew.Mittel wird dann im gegebenen Quell-Kontext unterschiedlich gewertet, als zB.:
- Mittelpunkt oder Schwerpunkt
- arithmetisches Mittel (nur bei Folgen im R1)
- Gleichgewicht bei stat.Momenten
- Geschlossene Richtungs-Polygon-Züge ( Sum(di)=0 )
Dieser Sachverhalt wird folgend am Beispiel 2-er Elemente beschrieben.
Mittelpunkt zweier Elemente p1,p2:
Sind nur die Ort-Koord. zu vermitteln, dann wird ein Punkt x auf der Geraden duch (p1,p2) gesucht, so dass die jeweiligen Abstände (Richtungs-Diff.) der Punkte zu x gleich sind.
Sind p1 und p2 zusätzlich noch mit einem Faktor gewichtet, so werden 2 Rechteck-Flaechen gesucht, f(*p1-x) und g*(p2-x), die von der Fläche her gleich sind,, also: f(p1-x)+g(p2-x)=0.
==> Gl.1.1: f*p1 +g*p2 -(f+g)*x=0
Bemerkung: Da es sich bei Punkt-Differenzen, z.B. (p1-x), um Richtungen handelt, werden Produkte von reellen Zahlen * Richtung auch als "stat.Moment" bezeichnet, welches betragsmäßig einer Rechteck-Fläche entspricht. Sind p1,p2 reelle Zahlen, z.B. Koord. der Punkte, so vereinfacht sich Gl.1.1 zu dem bekannten arithmetischen Mittel:
x =(f*p1 +g*p1/(f+g) , f,g,p1,p2 reell
Sind die Punkte gleich-gewichtet : f=g oder neutral-gewichtet: f=g=1, dann gilt: x=(p1+p2)/2
Gewichtetes Mittel p1,p2:
Bild , Temp-niv1.jpg
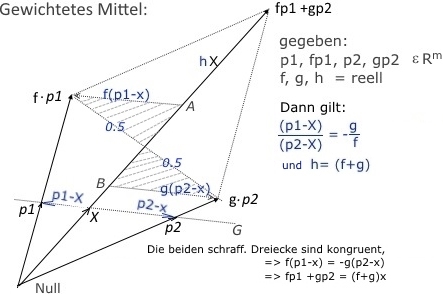
Alle Punkte p1,p2,fp1,gp2,Null liegen in einer Ebene.
Die 4 Dreiecke: D1=(0,x,p1) ,D1a=(0,A,fp1)
und D2=(0,x,p1) ,D2a=(0,B,gp2) sind paarweise aehnlich:
D1a =f*D1 und D2a =g*D2
Auch fuer die zu (p1-x) parallele Richtung (fp1-A) gilt dann (fp1-A) =f(p1-x).
Die Diagonalen des Parallelogramms schneiden sich in der Mitte. Dadurch sind die schraff.Dreiecke kongruent(1 Seite gleich und alle Winkel). Dadurch sind auch die beiden Richtungen f(p1-x) und g(p2-x) gleich (bis auf Vz.).
Also gilt: f(p1-x) +g(p2-x) =Null
x liegt allg. nicht in der Mitte von (p1-p2)
(p1-x)= [(f+g)*p1 -(f*p1+g*p2)]/(f+g)
= g*(p1-p2) /(f+g)
(p2-x)= [(f+g)*p2 -(f*p1+g*p2)]/(f+g)
= f*(p2-p1) /(f+g)
Aus (p1-x)/(x-p2) = g/f folgt:
Gl.1.2: f*(p1-x) = g*(x-p2) Der Mittelpunkt(Schwerpunkt) verschiebt sich in Richtung groesseres Gewicht, (hier f)!
Wichtig: Neben den Gewichten f,g der Punkte p1,p2 hat natürlich auch der Pkt. x ein neues Gewicht, nämlich h=(f+g). (f+g)*x ist dann als neuer, gewichteter Punkt zu verwenden, in Ersetzung des Punkte-Systems {f*p1, g*p2}.
Bemerkung: Gl.1.2 drueckt eine Form der Hebel-Gesetze aus: "Last*Lastarm = Kraft*Kraftarm"
Mittelpunkt mehrerer Elemente p1,p2,...:
Die Elemente mit den Orten {p1,p2,...} haben die Gewichte {f1,f2,...}
p' sei dann der Ort des gew.Mittel (Schwerpunkt) von f1*p1,f2*p2. p' hat dann das Gesamtgewicht der Pkte. p1,p2 als Gewichtung fuer weitere Berechnungen p'=(f1+f2)*p'.
Iterativ: Wird ein weiterer Pkt. z.B. f3*p3, mit (f1+f2)*p' gemittelt, so ergibgt sich als neuer gew.Mittelpunkt:
p''=((f1+f2)*p' +f3*p3) /(f1+f2+f3)p' durch (f1*p1 + f2*p2) / (f1+f2) ersetzen
p''= (f1*p1 +f2*p2 +f3*p3*) /(f1+f2+f3)
Weitere Mittlungen mit p'' vornehmen usw.
Allg. fuer n-Elemente: m= Sum(fi*pi)/Sum(fi)
Allg. Berechnung mehrerer Elemente p1,p2,...:
Gegeben sei {fj*pj} , j=1,...n , n≥1
Null-Differenz-Summe: sum(fj*pj - fj*pj) =0
=> sum(fj*pj - fj*X) =0 Bestimmungs-Gleichung für ein Element X
=> sum(fj*pj) - sum(fj)*X =0
Folgerung:
Bilden in der Punktfolge {fi*pi} die pi ebenfalls eine lineare Folge, also reelle Zahlen, (z.B. bei einer Koord.Einschränkung), dann hat man eine Folge von 2-er Tupeln reeller Zahlen. Geometrisch kann man dies dann als (diskrete) Abbildung im R² interpretieren und in einem (x,y)-Graph darstellen. Die Anordnung der f(i) oder p(i) als Quell-Menge oder Ziel-Menge spielt dabei keine Rolle:
f(i)=Abb(p(i) oder p(i)=Abb-1(f(i)
In dem Graph entstehen 2-dim Punkt-Mengen, {p(i),f((i)} oder {f(i),p((i)}, deren gew. Mittel (Durchschnitte) mit der allg. Gleichgewichts-Formel: Gl.1.3: sum(p(i)*f(i)) =sum(p(i))*x statistisch ausgewertet werden koennen.
Bei der Assoziierung von Objekt-Eigenschaften geht es darum, gleiche Eigenschaften, die in Messreihen vorliegen (bei uns Temp.-Messungen), in spez. Element-Folgen des Eukl.Raumes zu ueberfuehren.
M={fi*pi)} sei eine solche spezielle Elementfolge. Diese Form ist keine Einschränkung der Allgemeinheit, da jede Folge {pi)} auch gleichzeitig spez.Folge: {1*pi)} ist.
Begriffsbildung und Sachverhalt:
Bei den Begriffen: Mittel-, Gleichgewichts-, Schwer-punkt etc. handelt es sich im Allgemeinen immer um den gleichen Sachverhalt, nämlich:
Berechnung des gewichteten Mittels einer Folge M={fi*pi} .
Dieses gew.Mittel wird dann im gegebenen Quell-Kontext unterschiedlich gewertet, als zB.:
- Mittelpunkt oder Schwerpunkt
- arithmetisches Mittel (nur bei Folgen im R1)
- Gleichgewicht bei stat.Momenten
- Geschlossene Richtungs-Polygon-Züge ( Sum(di)=0 )
Dieser Sachverhalt wird folgend am Beispiel 2-er Elemente beschrieben.
Mittelpunkt zweier Elemente p1,p2:
Sind nur die Ort-Koord. zu vermitteln, dann wird ein Punkt x auf der Geraden duch (p1,p2) gesucht, so dass die jeweiligen Abstände (Richtungs-Diff.) der Punkte zu x gleich sind.
Sind p1 und p2 zusätzlich noch mit einem Faktor gewichtet, so werden 2 Rechteck-Flaechen gesucht, f(*p1-x) und g*(p2-x), die von der Fläche her gleich sind,, also: f(p1-x)+g(p2-x)=0.
==> Gl.1.1: f*p1 +g*p2 -(f+g)*x=0
Bemerkung: Da es sich bei Punkt-Differenzen, z.B. (p1-x), um Richtungen handelt, werden Produkte von reellen Zahlen * Richtung auch als "stat.Moment" bezeichnet, welches betragsmäßig einer Rechteck-Fläche entspricht. Sind p1,p2 reelle Zahlen, z.B. Koord. der Punkte, so vereinfacht sich Gl.1.1 zu dem bekannten arithmetischen Mittel:
Sind die Punkte gleich-gewichtet : f=g oder neutral-gewichtet: f=g=1, dann gilt: x=(p1+p2)/2
Gewichtetes Mittel p1,p2:

Alle Punkte p1,p2,fp1,gp2,Null liegen in einer Ebene.
Die 4 Dreiecke: D1=(0,x,p1) ,D1a=(0,A,fp1)
und D2=(0,x,p1) ,D2a=(0,B,gp2) sind paarweise aehnlich:
D1a =f*D1 und D2a =g*D2
Auch fuer die zu (p1-x) parallele Richtung (fp1-A) gilt dann (fp1-A) =f(p1-x).
Die Diagonalen des Parallelogramms schneiden sich in der Mitte. Dadurch sind die schraff.Dreiecke kongruent(1 Seite gleich und alle Winkel). Dadurch sind auch die beiden Richtungen f(p1-x) und g(p2-x) gleich (bis auf Vz.).
Also gilt: f(p1-x) +g(p2-x) =Null
x liegt allg. nicht in der Mitte von (p1-p2)
(p1-x)= [(f+g)*p1 -(f*p1+g*p2)]/(f+g)
= g*(p1-p2) /(f+g)
(p2-x)= [(f+g)*p2 -(f*p1+g*p2)]/(f+g)
= f*(p2-p1) /(f+g)
Aus (p1-x)/(x-p2) = g/f folgt:
Gl.1.2: f*(p1-x) = g*(x-p2) Der Mittelpunkt(Schwerpunkt) verschiebt sich in Richtung groesseres Gewicht, (hier f)!
Wichtig: Neben den Gewichten f,g der Punkte p1,p2 hat natürlich auch der Pkt. x ein neues Gewicht, nämlich h=(f+g). (f+g)*x ist dann als neuer, gewichteter Punkt zu verwenden, in Ersetzung des Punkte-Systems {f*p1, g*p2}.
Bemerkung: Gl.1.2 drueckt eine Form der Hebel-Gesetze aus: "Last*Lastarm = Kraft*Kraftarm"
Mittelpunkt mehrerer Elemente p1,p2,...:
Die Elemente mit den Orten {p1,p2,...} haben die Gewichte {f1,f2,...}
p' sei dann der Ort des gew.Mittel (Schwerpunkt) von f1*p1,f2*p2. p' hat dann das Gesamtgewicht der Pkte. p1,p2 als Gewichtung fuer weitere Berechnungen p'=(f1+f2)*p'.
Iterativ: Wird ein weiterer Pkt. z.B. f3*p3, mit (f1+f2)*p' gemittelt, so ergibgt sich als neuer gew.Mittelpunkt:
p''=((f1+f2)*p' +f3*p3) /(f1+f2+f3)
p''= (f1*p1 +f2*p2 +f3*p3*) /(f1+f2+f3)
Weitere Mittlungen mit p'' vornehmen usw.
Allg. Berechnung mehrerer Elemente p1,p2,...:
Gegeben sei {fj*pj} , j=1,...n , n≥1
Null-Differenz-Summe: sum(fj*pj - fj*pj) =0
=> sum(fj*pj - fj*X) =0
=> sum(fj*pj) - sum(fj)*X =0
Bemerkung:
In der allg. Schwerpunkt-Gleichung: m= Sum(fi*pi)/Sum(fi)
bedeutet 'm' die Koord. des Mittel-Pkt. im Rm und Sum(fi) das Gesamtgewicht aller in die Berechnung einbezogener Punkte, welches jetzt auf der Koord. 'm' lastet!.
Dies ist also das Newton'sche Prinzip, Koerper bzw. Massen zur Berechnung durch ihre Massen- Mittelpunkte zu ersetzen.
In der allg. Schwerpunkt-Gleichung: m= Sum(fi*pi)/Sum(fi)
bedeutet 'm' die Koord. des Mittel-Pkt. im Rm und Sum(fi) das Gesamtgewicht aller in die Berechnung einbezogener Punkte, welches jetzt auf der Koord. 'm' lastet!.
Dies ist also das Newton'sche Prinzip, Koerper bzw. Massen zur Berechnung durch ihre Massen- Mittelpunkte zu ersetzen.
Folgerung:
Bilden in der Punktfolge {fi*pi} die pi ebenfalls eine lineare Folge, also reelle Zahlen, (z.B. bei einer Koord.Einschränkung), dann hat man eine Folge von 2-er Tupeln reeller Zahlen. Geometrisch kann man dies dann als (diskrete) Abbildung im R² interpretieren und in einem (x,y)-Graph darstellen. Die Anordnung der f(i) oder p(i) als Quell-Menge oder Ziel-Menge spielt dabei keine Rolle:
In dem Graph entstehen 2-dim Punkt-Mengen, {p(i),f((i)} oder {f(i),p((i)}, deren gew. Mittel (Durchschnitte) mit der allg. Gleichgewichts-Formel: Gl.1.3: sum(p(i)*f(i)) =sum(p(i))*x statistisch ausgewertet werden koennen.
1.2 Messreihen
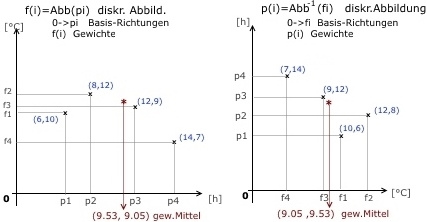
Beispiel fuer Messreihe (4 Temp.Messungen):
m={(p1,f1),(p2,f2),(p3,f3),(p4,f4)} ,pi =h ab 0Uhr
m={(6,10°),(8,12°),(12,9°),(14,7°)}
Es sind 2 Abbildungen möglich:
f(i)=Abb(p(i) oder p(i)=Abb-1(f(i)
1. f(i) = Abb(p(i)) , 0->p(i) Basis-Richtungen:
(10*6 +12*8 +9*12 +7*14) =(10+12+9+7)x
2. p(i) = Abb-1(f(i)) , 0->f(i) Basis-Richtungen:
(10*6 +12*8 +9*12 +7*14) =(6+8+12+14)x
zu 1.: linkeSum(362) = 38° *x[h] => x=9,53[h]
zu 2.: linkeSum(362) = 40[h] *x° => x=9,05[°C]
Als Ergebnis erhalten wir den Schwerpunkt der Folge
m={(p(i),f(i)) zu:
x=(9.53,9.05) ,siehe Abb(p(i))
Der Leser wird sich jetzt fragen: "Ist im Schwerpunkt x=(x1,x2) =(9.53h,9.05°) der x2-Wert (9.05°) der gesuchte Temp.Durchschnitt ja oder nein ?". Die Antwort lautet: Im Prinzip "ja", aber der x2-Wert ist stark abhängig von der Folge {p1,..,p4}. Jede Werte-Änderung in den {pi} bringt einen anderen Temp.-Durchschnitt x2, auch wenn die zugehörige Folge {fi} gleich bleibt!
Anders formuliert:
Ein Tages-Temp.-Durchschnitt lässt sich mit einer zufälligen Folge von Messungen während des Tages nicht korrekt ermitteln!
Normalisierung der Folge {pi*fi}:
Wenn die Messungen alle in gleichen Abständen erfolgen, kann p1=p2=....=pn=p gesetzt werden, und es kann der Faktor p ausgeklammert werden:
{pi}=p*{1,1,...1}
Die Gleichgewichts-Formel für p{1*fi} lautet dann:
p(1*f(1) +...+1*f(n)) -p(1+...+1) =0
=>Gl.2: sum(1*f(i)) = (n*1)x , i=1...n
Das ist eine Formel, die nur noch von den f(i) und der Anzahl "i" (=Messungen) abhaengt.
Messreihen fuer kontinuierliche Prozesse:
Viele Objekt-Eigenschaften sind stetige Funktionen ueber einen zeitlichen Verlauf. Durch Messreihen in Form von Folgen: {(Zeit,Wert)}, können solche Objekt-Eigenschaften statistisch ausgewertet werden.
In unserem Kontext betrifft das Temperatur-Messungen zu verschiedenen Zeitpunkten in einer lokalen Umgebung (um Sensor).
Temperatur-Verläufe unterliegen bestimmten Zyklen, z.B. täglich oder jährlich. Darüberhinaus müssen sie in ihren Abständen dem tatsächlichen Temp.-Verlauf möglichst nahe kommen, um vernünftige Durchschnitte zu berechnen.
Temperatur-Steigungen und -Abkühlungen verlaufen allg. relativ träge und nicht sprunghaft. Der max. gemessene Temp.-Gradient am Sensor(2.10.2015) betrug in 8h 17,5° =2,18°/h. Dies ist aber ein absoluter Ausnahme-Wert, der innerhalb von 3 Jahren noch nicht wieder erreicht wurde.
Für sinnvolle Auswertungen reichen deshalb Messungen aller 30min =48/Tag. (Theoretisch sind die Sensoren, in der Lage, alle 10msec einen Wert zu liefern!)
Die Datensammlung erfolgt durch zyklischen Übertragen der Messwerte alle 30' in eine SQL-DB im Internet als fortschreitende Folge:
m = {("ddd ttmmjjjj hh:mm:ss", "99.99°")}
Zur Verarbeitung werden die Daten, wie zuvor beschrieben, in eine normalisierte Folge {("Zeit","Wert")} konvertiert, mit streng-definierten, festen Abständen von 0,5h. Bei der Konvertierung müssen mögliche Lücken u. mehrfach-Messungen in der Quell-Folge durch Interpolation ausgeglichen werden.
Es sind 2 Abbildungen möglich:
zugehöriger (x,y)-Graph:
Bild , Temp-niv2.jpg
Berechnen des 'gew.Mittel' x nach allg. Gleichgewichts-Formel(Gl.1.3):
sum(p(i)*f(i)) =sum(p(i))*x

1. f(i) = Abb(p(i)) , 0->p(i) Basis-Richtungen:
(10*6 +12*8 +9*12 +7*14) =(10+12+9+7)x
2. p(i) = Abb-1(f(i)) , 0->f(i) Basis-Richtungen:
(10*6 +12*8 +9*12 +7*14) =(6+8+12+14)x
zu 1.: linkeSum(362) = 38° *x[h] => x=9,53[h]
zu 2.: linkeSum(362) = 40[h] *x° => x=9,05[°C]
Als Ergebnis erhalten wir den Schwerpunkt der Folge
m={(p(i),f(i)) zu:
Der Leser wird sich jetzt fragen: "Ist im Schwerpunkt x=(x1,x2) =(9.53h,9.05°) der x2-Wert (9.05°) der gesuchte Temp.Durchschnitt ja oder nein ?". Die Antwort lautet: Im Prinzip "ja", aber der x2-Wert ist stark abhängig von der Folge {p1,..,p4}. Jede Werte-Änderung in den {pi} bringt einen anderen Temp.-Durchschnitt x2, auch wenn die zugehörige Folge {fi} gleich bleibt!
Anders formuliert:
Ein Tages-Temp.-Durchschnitt lässt sich mit einer zufälligen Folge von Messungen während des Tages nicht korrekt ermitteln!
Normalisierung der Folge {pi*fi}:
Wenn die Messungen alle in gleichen Abständen erfolgen, kann p1=p2=....=pn=p gesetzt werden, und es kann der Faktor p ausgeklammert werden:
Die Gleichgewichts-Formel für p{1*fi} lautet dann:
=>
Das ist eine Formel, die nur noch von den f(i) und der Anzahl "i" (=Messungen) abhaengt.
Messreihen fuer kontinuierliche Prozesse:
Viele Objekt-Eigenschaften sind stetige Funktionen ueber einen zeitlichen Verlauf. Durch Messreihen in Form von Folgen: {(Zeit,Wert)}, können solche Objekt-Eigenschaften statistisch ausgewertet werden.
In unserem Kontext betrifft das Temperatur-Messungen zu verschiedenen Zeitpunkten in einer lokalen Umgebung (um Sensor).
Temperatur-Verläufe unterliegen bestimmten Zyklen, z.B. täglich oder jährlich. Darüberhinaus müssen sie in ihren Abständen dem tatsächlichen Temp.-Verlauf möglichst nahe kommen, um vernünftige Durchschnitte zu berechnen.
Temperatur-Steigungen und -Abkühlungen verlaufen allg. relativ träge und nicht sprunghaft. Der max. gemessene Temp.-Gradient am Sensor(2.10.2015) betrug in 8h 17,5° =2,18°/h. Dies ist aber ein absoluter Ausnahme-Wert, der innerhalb von 3 Jahren noch nicht wieder erreicht wurde.
Für sinnvolle Auswertungen reichen deshalb Messungen aller 30min =48/Tag. (Theoretisch sind die Sensoren, in der Lage, alle 10msec einen Wert zu liefern!)
Die Datensammlung erfolgt durch zyklischen Übertragen der Messwerte alle 30' in eine SQL-DB im Internet als fortschreitende Folge:
m = {("ddd ttmmjjjj hh:mm:ss", "99.99°")}
Zur Verarbeitung werden die Daten, wie zuvor beschrieben, in eine normalisierte Folge {("Zeit","Wert")} konvertiert, mit streng-definierten, festen Abständen von 0,5h. Bei der Konvertierung müssen mögliche Lücken u. mehrfach-Messungen in der Quell-Folge durch Interpolation ausgeglichen werden.
1.3 Durchschnitt einer normalisierten Folge {(p1,fi)}
Beispiel für Messreihe mit 48Werte/Tag:
Tag mit max. Temp.-Gradient in 8h:
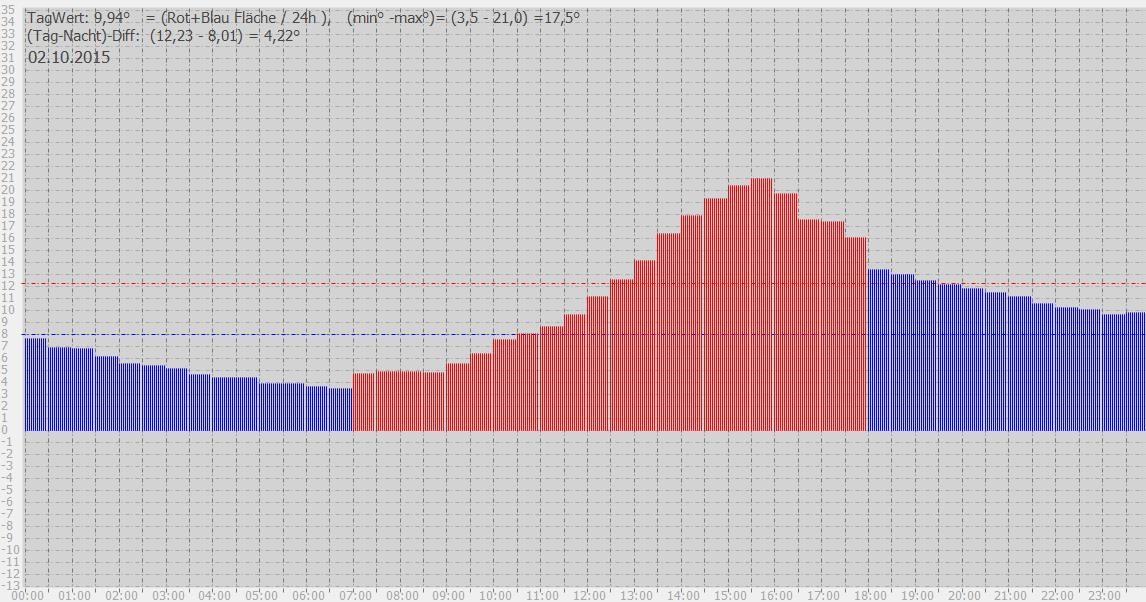
Wir berechnen den Durchschnitt nach Gleichgewichts-Formel Gl.2 aus Abschnitt 1.2 zuvor:
sum(1*f(i)) = (n*1)x , i=1...n
Die linke Summe stellt die Addition der Rechteck-Flächen von 0->48 [0.5h] dar, die rechte Seite gibt die Summe =Anzahl der Abstände zurück (hier 48x).
Die Gesamt-Rechteck-Summe für 48_Mess. ergibt 487,63°, was einem Tages-Durchschnitt von 10,159°C entspricht (liegt genau zwischen roter- und blauer-Linie in Grafik).
Fehlerabschätzung:
1. Bei den einzelnen Rechtecken wird der Messwert links angesetzt. Das hat zur Folge, dass zum tatsächlichen Verlauf bei steigenden Temperaturen Unter-Summen und bei fallenden Temperaturen Ober-Summen berechnet werden. Da über einen langen Zeitraum (z.B. 1Jahr) das Verhältnis der steigenden Summen zu den fallenden Summen gegen 0,5 strebt, gleichen sich die Diff. zwischen Ober- und Unter-Summen aus.
2. Es fehlt noch eine Abschätzung zum Verlauf innerhalb eines Abstandes (hier 0.5h):
Temperatur-Änderungen an der Erd-Oberfläche in lokalen Umgebungen sind relativ träge (deshalb 0.5h Abstands-Messungen). Darüberhinaus treten Wendepunkte(>±1°) im Temp.Verlauf am Tag nur relativ isoliert, also in grösseren Abständen, auf, so dass man in der überwiegenden Mehrzahl der Abstände von einem Temp.-Verlauf zwischen 'links-Messwert' und 'rechts-Messwert' innerhalb Abstand ausgehen kann. Dadurch kann der stetige Temp.-Verlauf ohne größeren Genauigkeits-Verlust problemlos durch eine "gerade Linie" ersetzt werden. Diese Vorgehensweise entspricht genau dem Ausgleich zwischen Ober- und Unter-Summen, wie er unter Pkt.1 zuvor beschrieben wird.
Bei dieser Betrachtung fehlen noch die "Wendepunkte": Hier findet ebenfalls ein gewisser Diff.-Ausgleich statt, da jeder "Wendepunkt nach oben" den vorhergehenden "Wendepunkt nach unten" ausgleicht und umgekehrt.
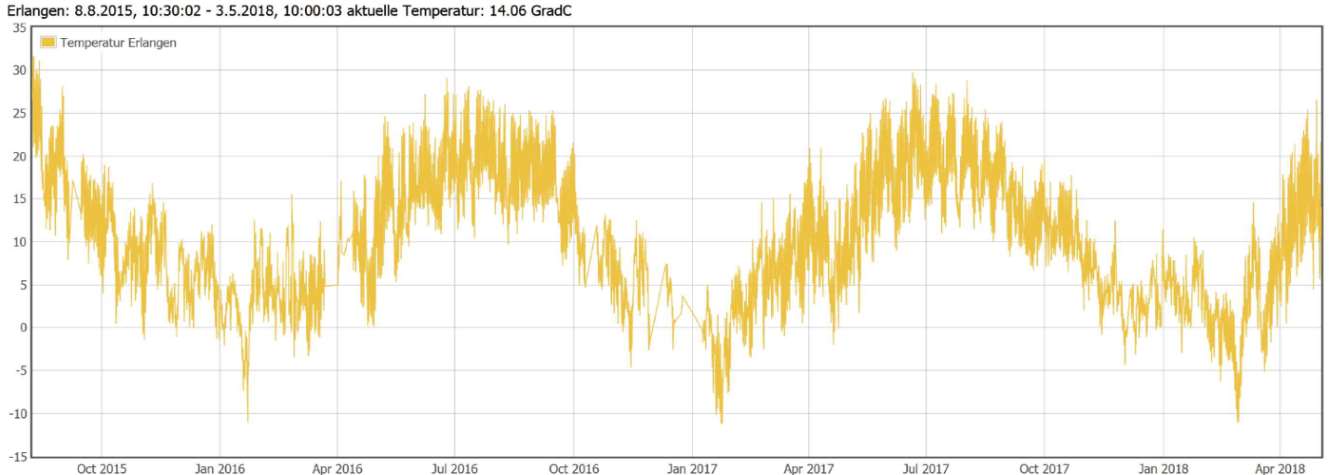
Temp-Verlauf über 3 Jahre in Erlangen:
Bild , Temp-niv3.jpg
Folgerung:
Insbesondere der Jahres-Temp.-Durchschnitt hat eine große Aussagekraft, da hier alle astronomischen Einflüsse auf den Temp.Verlauf ausgeglichen sind:
- Sonnenstand, von 17° - 63,8° über Horizont
- Jahreszeiten
- gleiche Tages- und Nachtzeiten
- Sonnennähe: 147.1 , Sonnenferne: 152.1 [km6]
Dadurch kann der sog. 365-Tage Durchschnitt als Temperatur-Niveau gewertet werden, welcher im Verlauf der Zeit steigt, fällt oder gleich bleibt (Stichwort Klima-Wandel)!
Tag mit max. Temp.-Gradient in 8h:

Wir berechnen den Durchschnitt nach Gleichgewichts-Formel Gl.2 aus Abschnitt 1.2 zuvor:
sum(1*f(i)) = (n*1)x , i=1...n
Die linke Summe stellt die Addition der Rechteck-Flächen von 0->48 [0.5h] dar, die rechte Seite gibt die Summe =Anzahl der Abstände zurück (hier 48x).
Die Gesamt-Rechteck-Summe für 48_Mess. ergibt 487,63°, was einem Tages-Durchschnitt von 10,159°C entspricht (liegt genau zwischen roter- und blauer-Linie in Grafik).
Fehlerabschätzung:
1. Bei den einzelnen Rechtecken wird der Messwert links angesetzt. Das hat zur Folge, dass zum tatsächlichen Verlauf bei steigenden Temperaturen Unter-Summen und bei fallenden Temperaturen Ober-Summen berechnet werden. Da über einen langen Zeitraum (z.B. 1Jahr) das Verhältnis der steigenden Summen zu den fallenden Summen gegen 0,5 strebt, gleichen sich die Diff. zwischen Ober- und Unter-Summen aus.
2. Es fehlt noch eine Abschätzung zum Verlauf innerhalb eines Abstandes (hier 0.5h):
Temperatur-Änderungen an der Erd-Oberfläche in lokalen Umgebungen sind relativ träge (deshalb 0.5h Abstands-Messungen). Darüberhinaus treten Wendepunkte(>±1°) im Temp.Verlauf am Tag nur relativ isoliert, also in grösseren Abständen, auf, so dass man in der überwiegenden Mehrzahl der Abstände von einem Temp.-Verlauf zwischen 'links-Messwert' und 'rechts-Messwert' innerhalb Abstand ausgehen kann. Dadurch kann der stetige Temp.-Verlauf ohne größeren Genauigkeits-Verlust problemlos durch eine "gerade Linie" ersetzt werden. Diese Vorgehensweise entspricht genau dem Ausgleich zwischen Ober- und Unter-Summen, wie er unter Pkt.1 zuvor beschrieben wird.
Bei dieser Betrachtung fehlen noch die "Wendepunkte": Hier findet ebenfalls ein gewisser Diff.-Ausgleich statt, da jeder "Wendepunkt nach oben" den vorhergehenden "Wendepunkt nach unten" ausgleicht und umgekehrt.
Hinweis:
Die hier beschriebe Auswertung einer normalisierten (Zeit-Wert)-Folge mit Fehlerabschätzung funktioniert nur sinnvoll bei der speziellen, zugrundeliegenden stetigen-Objekt-Eigenschafts-Folge: "Temperatur-Messung an Erdoberfläche in einer lokalen Umgebung"
Der Temp.Verlauf auf unserem Breitenkreis (Deutschland /Mitteleuropa) folgt angenähert einer "harmonischen Funktion der Zeit", im Eukl.Raum assoziert als "mehrfach-überlagerten Sinus-Funktionen".
Siehe dazu nachfolgendes Bild:
Die hier beschriebe Auswertung einer normalisierten (Zeit-Wert)-Folge mit Fehlerabschätzung funktioniert nur sinnvoll bei der speziellen, zugrundeliegenden stetigen-Objekt-Eigenschafts-Folge: "Temperatur-Messung an Erdoberfläche in einer lokalen Umgebung"
Der Temp.Verlauf auf unserem Breitenkreis (Deutschland /Mitteleuropa) folgt angenähert einer "harmonischen Funktion der Zeit", im Eukl.Raum assoziert als "mehrfach-überlagerten Sinus-Funktionen".
Siehe dazu nachfolgendes Bild:

Folgerung:
Insbesondere der Jahres-Temp.-Durchschnitt hat eine große Aussagekraft, da hier alle astronomischen Einflüsse auf den Temp.Verlauf ausgeglichen sind:
- Sonnenstand, von 17° - 63,8° über Horizont
- Jahreszeiten
- gleiche Tages- und Nachtzeiten
- Sonnennähe: 147.1 , Sonnenferne: 152.1 [km6]
Dadurch kann der sog. 365-Tage Durchschnitt als Temperatur-Niveau gewertet werden, welcher im Verlauf der Zeit steigt, fällt oder gleich bleibt (Stichwort Klima-Wandel)!
Weitere Betrachtungen zu Math.Problemen:
Euklidische Geometrie ,
Modell der reellen Zahlen ,
analytische Geometrie I ,
analytische Geometrie II ,
Euklidischer Raum ,
Analysis 1, Abbildungen ,
kleinere Beispiele der Himmelsmechanik im Newton-Modell ,
Bewegungen im Newton-Raum ,