| 4. Geometr.Objekte im Euklid. Raum, lin.Abbild. zurück ->2.Euklid.Geometrie |
Ausgangspunkt
Der m-dim abstrakte Euklid. Raum Rm ist die Menge aller m-Tupel
reeller Zahlen.
Symb.: Rm ={x: x=(x1,...,x(n)) , x(i)=reell }.
Wichtigstes Instrument zur Beschreibung geometr. Objekte im Rm sind "Richtungen". Dabei ist die Richtung kein eigentliches Element des eukl. Raumes, sondern eine Interpretation der Linearkombination L() aus Elementen oder Punkten des Raumes. z.B. bedeutet C=A+B ,A,B,C∈Rm folgendes:
1. C ist ein Punkt mit C=(a1+b1,...,a(m)+b(m))
2. (A+B) ist eine Zentral-Richtung von Null -> Pkt.C
3. (A-B) würde in diesem Kontext eine freie Richtung von B nach A bezeichnen.
4. Allgemein ist jeder Punkt X auch Richtung, nämlich: (Null,X)=(X-Null), also Richtung von Null nach X. Hierbei spricht man von einer gebundenen Richtung (an einen bestimmten Punkt), bei Null ist es die Zentral-Richtung.
Um nun geometr. Objekte positionieren und untersuchen zu können, wird mit einer festgelegten Menge von Richtungen der Raum gerastert, siehe Abschnitt 1.6 Eukl. Geometrie, und so eine genormte Richtungs-Basis geschaffen. Mit dieser Richtungs-Basis werden dann Pfade =L() zu den einzelnen Punkten oder Objekten geschlagen oder diese beschrieben.
An zulässigen Verknüpfungen kommen bei den Punkten (Elemente des Rm) nur L(), Norm(), Skapro() und V() in Frage, siehe Abschnitt 3.12 Zusammenfassung Reelle Zahlen. (zusätzlich Kreuz-Produkt 2-er Richtungen im R3). Mit reellen Zahlen als Koeff., Faktoren, usw. ist dagegen die gesamte Funktionalität der Analysis möglich.
In dieser Abhandlung kommt es nicht darauf an, alle Wissenszweige der Analyt.Geometrie anzusprechen, sondern nur die, wie man heute sagt, "Basics"... , den wesentlichen Kern und die Gründe, warum sich das in die eine oder andere Richtung entwickelt hat.
Ähnlich wie die Eukl.Geometrie Voraussetzung für die Entwicklung der gesamten Mathematik war, ist die Analyt.Geometrie logische Fortführung, im Zusammemschluß mit der Entwicklung des Modells der reellen Zahlen, dieses menschlichen Erkenntnisprozesses, der unter Anderem eben mit dieser anschaulichen, antiken Geometrie begonnen hat.
Der entscheidente Wendepunkt in der Math.Entwicklung war die Entdeckung des Prinzips der Grenzübergänge, welches erst die ganzen Zweige der höheren Mathematik ermöglichte. Darüber hinaus macht der immer wiederkehrende Rückgriff auf die geometr.Deutung von Sachverhalten, Relationen oder allg. gesagt Wechselwirkungen zwischen math./phys. Größen/Ereignissen, die Analyt. Geometrie so enorm wichtig im weiteren Erkenntnisprozess.
Die methodische Herangehensweise ist, wie in den anderen Abhandlungen auch, das abstrakte Kalkül, basierend auf Axiomen, Def., Sätzen, Beweise(direkt, indirekt, voll.Induktion), Folgerungen und Bemerkungen (,die auf Sachverhalte in übergeordneten Kontext hinweisen).
An Voraussetzungen werden eigentlich keine Anforderungen gestellt, höchstens allgemein math. Schulwissen ab 6.Klasse bis max. 12.Klasse (in Einzelfällen).
Beginnen wollen wir wieder mit dem einfachsten geometr.Objekt, dem Dreieck, siehe folgend!
Symb.: Rm ={x: x=(x1,...,x(n)) , x(i)=reell }.
Wichtigstes Instrument zur Beschreibung geometr. Objekte im Rm sind "Richtungen". Dabei ist die Richtung kein eigentliches Element des eukl. Raumes, sondern eine Interpretation der Linearkombination L() aus Elementen oder Punkten des Raumes. z.B. bedeutet C=A+B ,A,B,C∈Rm folgendes:
1. C ist ein Punkt mit C=(a1+b1,...,a(m)+b(m))
2. (A+B) ist eine Zentral-Richtung von Null -> Pkt.C
3. (A-B) würde in diesem Kontext eine freie Richtung von B nach A bezeichnen.
4. Allgemein ist jeder Punkt X auch Richtung, nämlich: (Null,X)=(X-Null), also Richtung von Null nach X. Hierbei spricht man von einer gebundenen Richtung (an einen bestimmten Punkt), bei Null ist es die Zentral-Richtung.
Um nun geometr. Objekte positionieren und untersuchen zu können, wird mit einer festgelegten Menge von Richtungen der Raum gerastert, siehe Abschnitt 1.6 Eukl. Geometrie, und so eine genormte Richtungs-Basis geschaffen. Mit dieser Richtungs-Basis werden dann Pfade =L() zu den einzelnen Punkten oder Objekten geschlagen oder diese beschrieben.
An zulässigen Verknüpfungen kommen bei den Punkten (Elemente des Rm) nur L(), Norm(), Skapro() und V() in Frage, siehe Abschnitt 3.12 Zusammenfassung Reelle Zahlen. (zusätzlich Kreuz-Produkt 2-er Richtungen im R3). Mit reellen Zahlen als Koeff., Faktoren, usw. ist dagegen die gesamte Funktionalität der Analysis möglich.
In dieser Abhandlung kommt es nicht darauf an, alle Wissenszweige der Analyt.Geometrie anzusprechen, sondern nur die, wie man heute sagt, "Basics"... , den wesentlichen Kern und die Gründe, warum sich das in die eine oder andere Richtung entwickelt hat.
Ähnlich wie die Eukl.Geometrie Voraussetzung für die Entwicklung der gesamten Mathematik war, ist die Analyt.Geometrie logische Fortführung, im Zusammemschluß mit der Entwicklung des Modells der reellen Zahlen, dieses menschlichen Erkenntnisprozesses, der unter Anderem eben mit dieser anschaulichen, antiken Geometrie begonnen hat.
Der entscheidente Wendepunkt in der Math.Entwicklung war die Entdeckung des Prinzips der Grenzübergänge, welches erst die ganzen Zweige der höheren Mathematik ermöglichte. Darüber hinaus macht der immer wiederkehrende Rückgriff auf die geometr.Deutung von Sachverhalten, Relationen oder allg. gesagt Wechselwirkungen zwischen math./phys. Größen/Ereignissen, die Analyt. Geometrie so enorm wichtig im weiteren Erkenntnisprozess.
Die methodische Herangehensweise ist, wie in den anderen Abhandlungen auch, das abstrakte Kalkül, basierend auf Axiomen, Def., Sätzen, Beweise(direkt, indirekt, voll.Induktion), Folgerungen und Bemerkungen (,die auf Sachverhalte in übergeordneten Kontext hinweisen).
An Voraussetzungen werden eigentlich keine Anforderungen gestellt, höchstens allgemein math. Schulwissen ab 6.Klasse bis max. 12.Klasse (in Einzelfällen).
Beginnen wollen wir wieder mit dem einfachsten geometr.Objekt, dem Dreieck, siehe folgend!
Diese Abhandlung besteht aus folgenden Abschnitten:
4.0
Skalarprodukt und Dreieck ,Winkel
->4.0
4.0a
Skalarprodukt und Volumen-Produkt im Rm , Determinante
->4.0a
4.0b
Eigenschaften von (BxA) , Kreuzprodukt
->4.0b
4.0c
Teilungsverhältnis , Arithmetisches Mittel
->4.0c
4.1
Linearkombinationen
->4.1
4.2
Gerade, Ebene, Dreieck ,Fläche Parallelogramm
->4.2
4.3
Geometrische Orte im Rm
->4.3
4.4
Lineare Gleich. Systeme , Vektorraum , {L()=b} ∈ Topolog. Raum
->4.4
4.5
Der Lösungsraum linearer Gleichungs Systeme
->4.5
4.6
Koordinaten-Transformationen , gerade Achsen
->4.6
4.7
Geometr.Deutung der Linear-Kombination L()
->4.7
4.8
Geometr.Deutung des Gauß-Eliminierungs-Algorithmus
->4.8
4.9
Die Lineare Abbildung im Rm , Allg. Graph-Definition
->4.9
4.10
Auflösungs-Theorie
->4.10
4.0 Skalarprodukt und Dreieck:
Anknüpfungspunkt sind die Überlegungen im Abschnitt 1.9 "Zerlegung des Dreiecks in
2 rechtw.Dreiecke".
Bild , Anal-geo1.jpg
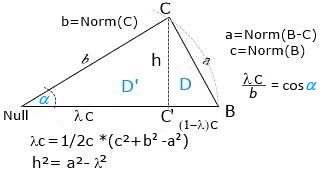
b² =Norm(C)² =c1² +c2² + ...
c² =Norm(b)² =b1² +b2² + ...
a² =Norm(B-C)² =(b1-c1)² +(b2-c2² + ...
Einsetzen in: λc =(c²+b² -a²)/2c :
=> c1² +c2² + ...+ b1² +b2² + ...
-b1² +2*b1*c1 -c1²
-b2² +2*b2*c2 -c2² + ....
=> b1*c1 +b2*c2 +... +b(m)*c(m)
Das ist das Skapro() zwischen den Richtungen B und C, also <C,B> .
Ergebnis: Das Skapro() gibt den Teilungspunkt für die Höhe h auf der Strecke (A,B) vor.
Im nächsten Bild werden 2 entartete Dreiecke gezeigt in Abhängigkeit vom Skapro(C,B) =λc =λ*d(Null,B):
Bild , Anal-geo2.jpg
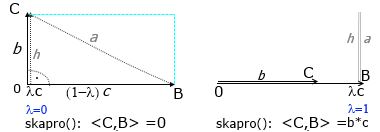
Im rechten Bild fällt die Richtung (0,C) auf die Richtung (0,B) zurück, also gleiche Richtung, und die Höhe h spielt keine Rolle mehr, ebenso das Volumenprodukt V(C*B), es verschwindet und wird formal mit Null bewertet.
Satz1: Ist das Skapro() zwischen 2 Richtungen =0, dann stehen die beiden Richtungen senkrecht aufeinander, ansonsten ist das Skapro()≠0 .
Proportionen im Dreieck:
Gegeben sei ein weiteres Dreieck D(a',b',c'), wobei gilt:
a'=f*a, b'=f*b, c'=f*c , dann sind alle Dreiecke mit f=reell
zum Dreieck D(a,b,c), siehe Bild: Anal-geo1.jpg, proportional =ähnlich,
so daß die Verhältnisse der Seiten h, λc, b untereinander als Maß für den Winkel im Pkt.A (α) genommen werden können:
Maß1(α): h /b , = sin((α)
Maß2(α): λc /b , = cos((α)
Maß3(α): h /λc , = tan((α)
Maß4(α): λc /h , = cot(α)
Beispiele:
Phytagoras: b² = h² +(λc)² /b²
=> 1= (h/b)² +(λc/b)²
=> 1= sin(α)² +cos(α)²
=> h/λc =(h/b) /(λc /b) = sin((α)/cos((α)
Cosinus-Satz im Dreieck:
Wir gehen nochmal zur Darstellung von λc im Bild zurück:
(b²+c² -a²)1/2 =λc² ,beide Seiten: *1/bc
=> (b²+c² -a²)1/2bc =λc²/bc =λc/b =cosα
=> (b²+c² -a²) =2bc*cosα
=> Cosinussatz: b²+c² -2bc*cosα =a²
Das ist der Phytagoras für schiefe Dreiecke, wenn α=90° wird, gilt;
b²+c² -2bc*0 =a² ,der richtige Phytagoras mit a als Hypothenuse.
Fläche Dreieck:
F= c*h/2 ,wegen h/b =sinα gilt:
F= 0.5c*b*sinα

b² =Norm(C)² =c1² +c2² + ...
c² =Norm(b)² =b1² +b2² + ...
a² =Norm(B-C)² =(b1-c1)² +(b2-c2² + ...
Einsetzen in: λc =(c²+b² -a²)/2c :
=> c1² +c2² + ...+ b1² +b2² + ...
-b1² +2*b1*c1 -c1²
-b2² +2*b2*c2 -c2² + ....
=> b1*c1 +b2*c2 +... +b(m)*c(m)
Das ist das Skapro() zwischen den Richtungen B und C, also <C,B> .
Ergebnis: Das Skapro() gibt den Teilungspunkt für die Höhe h auf der Strecke (A,B) vor.
Im nächsten Bild werden 2 entartete Dreiecke gezeigt in Abhängigkeit vom Skapro(C,B) =λc =λ*d(Null,B):

Im rechten Bild fällt die Richtung (0,C) auf die Richtung (0,B) zurück, also gleiche Richtung, und die Höhe h spielt keine Rolle mehr, ebenso das Volumenprodukt V(C*B), es verschwindet und wird formal mit Null bewertet.
Satz1: Ist das Skapro() zwischen 2 Richtungen =0, dann stehen die beiden Richtungen senkrecht aufeinander, ansonsten ist das Skapro()≠0 .
Bemerkung: Diese Aussage bzw. Eigenschaft ist enorm wichtig!
Sie sichert beim Übergang des abstrakt.-Euklid.-Raum zum konkreten Raum, z.B dem
lokalen Raum unserer Anschauung, die Orthogonalität der Dimensionen /Koord.
Proportionen im Dreieck:
Gegeben sei ein weiteres Dreieck D(a',b',c'), wobei gilt:
so daß die Verhältnisse der Seiten h, λc, b untereinander als Maß für den Winkel im Pkt.A (α) genommen werden können:
Maß2(α): λc /b
Maß3(α): h /λc
Maß4(α): λc /h
Phytagoras: b² = h² +(λc)²
=> 1= (h/b)² +(λc/b)²
=> 1= sin(α)² +cos(α)²
=> h/λc =(h/b) /(λc /b) = sin((α)/cos((α)
Cosinus-Satz im Dreieck:
Wir gehen nochmal zur Darstellung von λc im Bild zurück:
=> (b²+c² -a²)1/2bc =λc²/bc =λc/b =cosα
=> (b²+c² -a²) =2bc*cosα
=> Cosinussatz: b²+c² -2bc*cosα =a²
Fläche Dreieck:
F= 0.5c*b*sinα
4.0a Skalarprodukt und Volumen-Produkt im Rm:
Hat man eine Koord. Basis im Rm zugeordnet, werden die beiden zulässigen
multiplikativen Vernüpfungen im Rm: Skapro() und Vol() wie folgt def.
Skapro(p1,p2):
p1=(a1,...,a(m)) , p2=(b1,...,b(m)) sind 2 beliebige Richtungen, dann ist
Skapro(p1,p2)= a1*b1 + .... +a(m)*b(m)
Vol(p1p2....p(n)):
Das Volumen-Produkt aus n-Richtungen ist zunächst als normales Produkt der p(i) in Lin.Komb.Darstellung def., d.h. man bekommt eine Summe von m*n Teilprodukten p1(i1)*p2(i2)*....*p(n)(i(n) , wobei die Indizes i() in einer Folge sich durchaus wiederholen können.
Beispiel: (a1*e1 +a2*e2)*(b1*e1 +b2*e2)
= a1b1(e1e1) +a1b2(e1e2) +a2b1(e2e1) +a2b2(e2e2)
Da es sich hier um eine Vol.Berechnung handelt, sind die e(i)*e(j)=0 für i=j, weil gleiche Richtungen keine Fläche o.Volumen aufspannen.
==> Vol((a1,a2)*(b1,b2)) = a1b2(e1e2) +a2b1(e2e1) , wegen e2e1 = -e1e2 (Vertauschen von Richt.) und Fläche(e1*e2)=1 folgt:
Vol((a1,a2)*(b1,b2)) = a1b2 - a2b1
Def:
Hat man für Vol() von n-Richt. ein allg. Summen-Glied:
..... + (..)(±1)ke(i1)*..*e(i(n)) +...... ,
so gibt der Exponent k die Anzahl paarweiser Vertauschungen innerhalb der e(i1)*..*e(i(n)) an, um auf die Basis-Komb. e1*e2*e3*...*e(n) zu kommen.
Satz: Ohne Beweis sei folg. Aussage richtig: Es gibt genau n! Permutationen einer Indexfolge {12...n} , und davon ist genau die Hälfte, n!/2, negativ bewertet.
Beispiel:
123 , 231 , 312 sind positiv und
132 , 213 , 321 sind negativ bewertet.
Geometr.Deutung des Vol():
Um zu Beurteilen, ob beim Vol() von n-Richtungen im Rm etwas Sinnvolles herauskommt, also Vol() ≠0, muß man prüfen,in wie weit die Richtungen ein tatsächliches Volumen aufspannen, z.B. können 2-Richtungen im R³ max. eine Fläche ausbilden und kein 3-dim-Volumen.
Aussage1:
n>m , dann ist Vol()=0. Beispiel im R²:
3 Richt. (e1 +e2)*(e1 +e2)*(e1 +e2) ,die Koeff. lasse ich der Einfachheit
halber weg:
= (e1e1 +e1e2 +e1e2 +e1e2)*(e1 +e2)
= e1e1e1 +e1e2e1 +e1e2e1 +e1e2e1
+e1e1e2 +e1e2e2 +e1e2e2 +e1e2e2 =0
In jedem Summanden wiederholen sich mind. 2 Indizes!
Aussage2:
n<m , dann fehlen zum kompletten Vol. einige Richtungen, deshalb auch hier =0.
Aussage3:
n=m , hier sind gerade genug Richt. vorhanden. Diese müssten aber, anschaulich gesprochen, in alle Ecken des Rm zeigen, also wie weiter unten ausgeführt wird, "linear unabhängig" sein.
Spez.Fall Vol() im R²/R³:
2 Richtungen A,B im R³:
Bild , Anal-geo8.jpg

Im Ausdruck(1) ersetzen wir die Quadrate rts. in der Reihenfolge von lks. nach rechts durch D1, D2, D3 und erhalten für die Fläche F(PG) =sqrt(D1² +D2² +D3²)
Dies entspricht aber genau der Länge einer Richtung/Vektors mit den Koord.:
Z(z1,z2,z3) =(D1,D2,D3) , im Bild blau, mit Namen BxA, also Z=(BxA) und nennen diesen Vektor Flächenprodukt o. Kreuzprodukt zweier Richt./Vektoren im R2 /R3. In den Dim >3 kann man h² zwar genauso berechnen, aber das Ergebnis läßt keine geometr.Deutung mehr zu!
Das Flächen-Produkt (BxA) ist eine neue Verknüpfung in der Menge der m-Tupel reeller Zahlen (abstrakter Eukl.Raum) Rm, 2≤m≤3 ,zu den beiden, bereits zuvor def., Verknüpfungen Skapro() und Vol(p1...p(m)), {p(i)}= m-lin.unabhängige Richt.
Skapro(p1,p2):
Skapro(p1,p2)= a1*b1 + .... +a(m)*b(m)
Vol(p1p2....p(n)):
Das Volumen-Produkt aus n-Richtungen ist zunächst als normales Produkt der p(i) in Lin.Komb.Darstellung def., d.h. man bekommt eine Summe von m*n Teilprodukten p1(i1)*p2(i2)*....*p(n)(i(n) , wobei die Indizes i() in einer Folge sich durchaus wiederholen können.
= a1b1(e1e1) +a1b2(e1e2) +a2b1(e2e1) +a2b2(e2e2)
Da es sich hier um eine Vol.Berechnung handelt, sind die e(i)*e(j)=0 für i=j, weil gleiche Richtungen keine Fläche o.Volumen aufspannen.
==> Vol((a1,a2)*(b1,b2)) = a1b2(e1e2) +a2b1(e2e1) , wegen e2e1 = -e1e2 (Vertauschen von Richt.) und Fläche(e1*e2)=1 folgt:
Vol((a1,a2)*(b1,b2)) = a1b2 - a2b1
Def:
Hat man für Vol() von n-Richt. ein allg. Summen-Glied:
so gibt der Exponent k die Anzahl paarweiser Vertauschungen innerhalb der e(i1)*..*e(i(n)) an, um auf die Basis-Komb. e1*e2*e3*...*e(n) zu kommen.
Satz: Ohne Beweis sei folg. Aussage richtig: Es gibt genau n! Permutationen einer Indexfolge {12...n} , und davon ist genau die Hälfte, n!/2, negativ bewertet.
Beispiel:
123 , 231 , 312 sind positiv und
132 , 213 , 321 sind negativ bewertet.
Geometr.Deutung des Vol():
Um zu Beurteilen, ob beim Vol() von n-Richtungen im Rm etwas Sinnvolles herauskommt, also Vol() ≠0, muß man prüfen,in wie weit die Richtungen ein tatsächliches Volumen aufspannen, z.B. können 2-Richtungen im R³ max. eine Fläche ausbilden und kein 3-dim-Volumen.
Aussage1:
n>m , dann ist Vol()=0. Beispiel im R²:
= (e1e1 +e1e2 +e1e2 +e1e2)*(e1 +e2)
= e1e1e1 +e1e2e1 +e1e2e1 +e1e2e1
+e1e1e2 +e1e2e2 +e1e2e2 +e1e2e2 =0
In jedem Summanden wiederholen sich mind. 2 Indizes!
Aussage2:
n<m , dann fehlen zum kompletten Vol. einige Richtungen, deshalb auch hier =0.
Aussage3:
n=m , hier sind gerade genug Richt. vorhanden. Diese müssten aber, anschaulich gesprochen, in alle Ecken des Rm zeigen, also wie weiter unten ausgeführt wird, "linear unabhängig" sein.
Spez.Fall Vol() im R²/R³:
2 Richtungen A,B im R³:

Im Ausdruck(1) ersetzen wir die Quadrate rts. in der Reihenfolge von lks. nach rechts durch D1, D2, D3 und erhalten für die Fläche F(PG) =sqrt(D1² +D2² +D3²)
Dies entspricht aber genau der Länge einer Richtung/Vektors mit den Koord.:
Z(z1,z2,z3) =(D1,D2,D3) , im Bild blau, mit Namen BxA, also Z=(BxA) und nennen diesen Vektor Flächenprodukt o. Kreuzprodukt zweier Richt./Vektoren im R2 /R3. In den Dim >3 kann man h² zwar genauso berechnen, aber das Ergebnis läßt keine geometr.Deutung mehr zu!
Das Flächen-Produkt (BxA) ist eine neue Verknüpfung in der Menge der m-Tupel reeller Zahlen (abstrakter Eukl.Raum) Rm, 2≤m≤3 ,zu den beiden, bereits zuvor def., Verknüpfungen Skapro() und Vol(p1...p(m)), {p(i)}= m-lin.unabhängige Richt.
4.0b Eigenschaften von (BxA):
1. (BxA) =-(AxB),d.h. die Flächen-Berechnung, sogar die Berechn. aller
Flächen im Rm>1, hat eine Orientierung, änlich wie das schon beim Dreieck
in der "Eukl. Geometrie" angesprochen wurde, nämlich: Betrachtung eines PG von
Vorder- und Rückseite aus (vertauscht optisch die Reihenfolge der Seiten).
Beweis: Die Richtigkeit der Aussage überprüfen wir zunächst im R²:
A=(a1,a2) , B=(b1,b2) ,F(PG(A,B)) = a1b2-b1a2
F(PG(B,A)) = b1a2-a1b2 = -(a1b2 -b1a2) Qed.
2. Z=(BxA) steht senkr. zu A u. B, also senkr. auf PG.
Beweis:
Zum Beweis braucht man nur die Skapro(Z,A) und Skapro(Z,B) berechnen, diese müssen =0 sein. Matrix der 3 Richtungen A,B,Z ist:
( a1 a2 a3 )
( b1 b2 b3 )
( D3 D2 D1 )
Skapro(A,Z)) =a1*D3 +a2*D2 +a3*D1
a1(a2b3-b2a3) +a2(a1b3-b1a3) +a3(a1b2-b1a2)
= a1a2b3 -a1b2a3 +a2a1b3 -a2b1a3 +a3a1b2 -a3b1a2
1.und 3.Summand betraglich gleich
2.und 5.Summand betraglich gleich
4.und 6.Summand betraglich gleich
=> Skapro(A,Z)=0
Skapro(B,Z)) =b1*D3 +b2*D2 +b3*D1
b1(a2b3-b2a3) +b2(a1b3-b1a3) +b3(a1b2-b1a2)
= b1a2b3 -b1b2a3 +b2a1b3 -b2b1a3 +b3a1b2 -b3b1a2
1.und 6.Summand betraglich gleich
2.und 4.Summand betraglich gleich, aber beide -
3.und 5.Summand betraglich gleich, aber beide +
=> Skapro(B,Z) ≠0
Das Problem kann durch ersetzen von D2 mit -D2 gelöst werden.
D2= -(a1b3-b1a3) =(b1a3-a1b3)
Jetzt sind beide Skapro(A,Z) =Skapro(B,Z) =0
Der Vektor Z=(AxB):
= [(a2b3-b2a3),(b1a3-a1b3),( a1b2-b2a1)]
3. Jetzt ist noch zu klären, in welche Richtung Z=(AxB) zeigt:
Wir betrachten Z=(AxB) für die Projektion in [e1e2]-Ebene:
( a1 a2 0 )
( b1 b2 0 )
( D3 D2 D1 ) ,=> D3=0, D2=0, D1=(a1b2-b1a2)
=> die z3-Koord. von Z hat die gleiche Orientierung wie PG(A,B) nämlich (a1b2-b1a2), wechselt die Orientierung des PG zu PG(B,A)= (-a1b2+b1a2)= -((a1b2-b1a2)) so zeigt der Vektor Z nach unten, also nach -Z.
Def.: Z bildet beim Kreuz-Produkt mit zwei beliebigen anderen Richt./Vektoren ein sogenanntes "Rechts-System", d. h., Z,P,Q genügen der 3-Finger-Regel, oder: P kann mit kleinstem Winkel in Richtung Q gedreht, und Q mit kleinstem Winkel in Richtung Z gedreht werden. Werden P und Q vertauscht, gilt: (PxQ)= -(QxP)
(Drehrichtung immer math.pos., also entgegen Uhr-Zeiger-Sinn)
Das Vol() für A=(a1,a2,0), B=(b1,b2,0), Z=(0,0,D1) lautet: D1² ,d.h. Det() positiv, das bedeutet, das 3-er System (Z,A,B) mit Z=(AxB) bildet für beliebige Richtungen A,B oder B,A immer ein Rechts-System, also wie Koord.Achsen [x,y,z].
Beweis: Die Richtigkeit der Aussage überprüfen wir zunächst im R²:
A=(a1,a2) , B=(b1,b2) ,F(PG(A,B)) = a1b2-b1a2
F(PG(B,A)) = b1a2-a1b2 = -(a1b2 -b1a2) Qed.
2. Z=(BxA) steht senkr. zu A u. B, also senkr. auf PG.
Beweis:
Zum Beweis braucht man nur die Skapro(Z,A) und Skapro(Z,B) berechnen, diese müssen =0 sein. Matrix der 3 Richtungen A,B,Z ist:
( a1 a2 a3 )
( b1 b2 b3 )
( D3 D2 D1 )
Skapro(A,Z)) =a1*D3 +a2*D2 +a3*D1
a1(a2b3-b2a3) +a2(a1b3-b1a3) +a3(a1b2-b1a2)
= a1a2b3 -a1b2a3 +a2a1b3 -a2b1a3 +a3a1b2 -a3b1a2
1.und 3.Summand betraglich gleich
2.und 5.Summand betraglich gleich
4.und 6.Summand betraglich gleich
=> Skapro(A,Z)=0
Skapro(B,Z)) =b1*D3 +b2*D2 +b3*D1
b1(a2b3-b2a3) +b2(a1b3-b1a3) +b3(a1b2-b1a2)
= b1a2b3 -b1b2a3 +b2a1b3 -b2b1a3 +b3a1b2 -b3b1a2
1.und 6.Summand betraglich gleich
2.und 4.Summand betraglich gleich, aber beide -
3.und 5.Summand betraglich gleich, aber beide +
=> Skapro(B,Z) ≠0
Das Problem kann durch ersetzen von D2 mit -D2 gelöst werden.
D2= -(a1b3-b1a3) =(b1a3-a1b3)
Jetzt sind beide Skapro(A,Z) =Skapro(B,Z) =0
Der Vektor Z=(AxB):
= [(a2b3-b2a3),(b1a3-a1b3),( a1b2-b2a1)]
3. Jetzt ist noch zu klären, in welche Richtung Z=(AxB) zeigt:
Wir betrachten Z=(AxB) für die Projektion in [e1e2]-Ebene:
( a1 a2 0 )
( b1 b2 0 )
( D3 D2 D1 ) ,=> D3=0, D2=0, D1=(a1b2-b1a2)
=> die z3-Koord. von Z hat die gleiche Orientierung wie PG(A,B) nämlich (a1b2-b1a2), wechselt die Orientierung des PG zu PG(B,A)= (-a1b2+b1a2)= -((a1b2-b1a2)) so zeigt der Vektor Z nach unten, also nach -Z.
Def.: Z bildet beim Kreuz-Produkt mit zwei beliebigen anderen Richt./Vektoren ein sogenanntes "Rechts-System", d. h., Z,P,Q genügen der 3-Finger-Regel, oder: P kann mit kleinstem Winkel in Richtung Q gedreht, und Q mit kleinstem Winkel in Richtung Z gedreht werden. Werden P und Q vertauscht, gilt: (PxQ)= -(QxP)
(Drehrichtung immer math.pos., also entgegen Uhr-Zeiger-Sinn)
Das Vol() für A=(a1,a2,0), B=(b1,b2,0), Z=(0,0,D1) lautet: D1² ,d.h. Det() positiv, das bedeutet, das 3-er System (Z,A,B) mit Z=(AxB) bildet für beliebige Richtungen A,B oder B,A immer ein Rechts-System, also wie Koord.Achsen [x,y,z].
4.0c Teilungsverhältnis:
Streckenteilung:
Eine Stecke (AB) wird durch eine Faktor f, 0<f<1 in 2 Teilstrecken geteilt:
(AB) = f*(A-B) +(1-f)*(A-B)
Die Teilung soll entspr. der Gewichtung der Punkte A,B erfolgen:
f/(1-f) = A(m1)/B(m2) =m1/m2 => f*m2 =(1-f)*m1
f*m2 =m1 -f*m1 => f = m1/(m1+m2)
u.(1-f)=f*m2/m1 =>(1-f) =m2/(m1+m2)
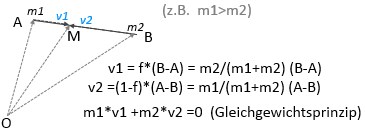
Das Gleichgewichts-Prinzip: m1*v1 = m2*v2 bedeutet, daß die um den Faktor m1,m2 gestreckten Richt. gleich sind.
Spez. Vektor-Arithmetik im Dreieck:
1. A=(a1,a2,..), B=b1,b2,...), C=(c1,c2,..) dazu existieren die folg. Richtungen:
(B-A)=(b1-a1, b2-a2,...), (C-B)=(c1-b1, c2-b2,...),
(A-C)=(a1-c1, a2-c2,...) => (B-A)+(C-B)+(A-C) =0,
d.h., Die Richt. bilden ein geschlossenes Seileck, also Dreieck.
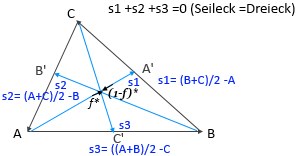
Entspr. Bild:
f*[(B+C)/2 -A] +f*[C-(A+B)/2] =(C-A)
f/2 *(B+C -2A +2C -A-B) =(C-A)
=> f/2*(3C -3A)=(C-A)
=> 3f/2*(C-A)=(C-A) => f=2/3
Da die anderen Kombinationen s1-s2 und s2-s3 auch f=2/3 ergeben, gilt folg. Fazit:
Satz: Die Seiten-Halbierenden im Dreick schneiden sich in einem Punkt M, der gleichzeitig Mittelpunkt /Schwerpunkt der Fläche Dreieck (ABC) ist.
Beweis:
Zum Schnittpunkt: 2/3(s1+s2+s3) =0 ,wegen s1+s2+s3=0 (siehe Bild).
B' ist Schwerpunkt von A,C, in B' sind also 2 Punkte gemittelt.
Für den Mittelpunkt. M' des Dreieckes ergibt sich der Ortsvektor zu f=2/3 auf der Richtung(B'B):
Aufteilung der Strecke(B'B) in f und (1-f) Teil:
(M'0) -2/3[B'B)] -B= f*(B'B) -(1-f)(B'B)
M' -2/3 *(A+B)/2 -B) -B =0 (Seileck!)
M'= 2/3[(A*B)/2 -B] +B
M'= 1/3 *(A+B+C)
Dies ist das arithmetische Mittel dreier Zahlen/Pkte. QED
Bemerkung:
Das arithmet.Mittel, allg. (A1+...+A(n)) /n, wird offensichtlich in allen Koord.Folgen getrennt berechnet. Das bedeutet, daß man das Mittel auch nur z.B. für eine Koord. berechnet, und man erhält sog. Schwerpunkt- Linien. Erst der Schnittpunkt. mehrerer, (mind.2), Schwerpunkt-Linien ergibt den gesamt-Schwerpunkt der Pkt.-Folge.
Deshalb reichte zuvor, bei der Ermittlung von f, bereits die Untersuchung von s1 und s2.
Halbierung eines Dreiecks:
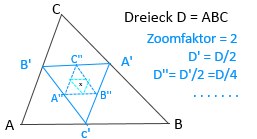
4.1 Linearkombinationen:
1. Basis-Richtungen:
Spezielle Richtungen im Rm sind:
e1 =(1,0,0,...,0)
e2 =(0,1,0,...,0)
e3 =(0,0,1,...,0) . . . . . em =(0,0,0,...,1)
Ein beliebiger Pkt.läßt sich dann als L() von {e(i)} i=1,...,m darstellen:
P= x1*e1 +x2*e2 +... +x(m)*e(m) , x(i) reell.
(Beweis: P=(x1,x2,x2,...,x(m) ) fest gewählt bis auf j-Koord. , dann L(x(j) = x(j) + e(j) bilden.
Diese Prozedur für alle j ergibt P=(x1*e1,...,x(m)*e(m) )
Sind alle x(i)=0 bis auf ein x(j)≠0, so verhält sich dieses x=x(j) wie eine reelle Zahl im R(1)j der Menge reeller Zahlen.
Die Multiplikation einer Richtung P mit einer reellen Zahl führt zu einer Streckung /Stauchung der Richtung:
Beispiel: P'= c*P, Norm(c*P) =c*Norm(P), also: abs(c)>1 Streckung, 1>abs(c) Stauchung.
Die skalare Multipl. der {e(i)} untereinander ergibt:
Skapro(e(i),e(j)) =0 ,∀i,j , i≠j
Skapro(e(i),e(i)) =1 ,∀i =1,...,m
Das V(e(1)***e(m)) = +1 , Maß eines m-dim norm.Eins-Würfel
Folgerung: Die Richtungen aus {e(i)} stehen paarweise senkrecht aufeinander. Sie bilden somit ein orthogonales-Eins-Richtungs-System im Rm.
Jeder Punkt P kann als Linearkombination von {e(i)} dargestellt werden:
P =(x1,x2,....,x(m)) ,x(i) reell, Koord. Darstellung
=L({e(i)}) =x1e1 +x2e2 +...+xmem
Die e(i) werden deshalb auch als Basis-Richtungen und die {e(i)} als Basis des Rm bezeichnet
2. Unterräume des Rm :
Setzt man in der Basis {e(i)} i=1,...,m eine oder mehrere e(i) auf Null, so reduziert sich die Menge der damit dargestellten Punkte zu einer Teilmenge =Unterraum Rm-k ,k=Anzahl der auf Null gesetzen Indizes j.
Beispiel: {e1, 0, e3} , R3-1 ={x: x=(x1*e1 +x2*0 +x3*e3) ,x(i)=reell }
Hier in dem Beispiel gibt es 3 verschiedene 2-dim Unterräume:
{0, e2, e3} ,{e1, 0, e3} ,{e1, e2, 0}
Folgerung1: Jeder Rn kann als Unterraum eines Rm ,m>n aufgefaßt werden. So ist jede reelle Zahl r gleichzeitig reelle Zahl und 1-dim Unterraum R1 , wie im Beispiel des R3 einmal als x-Koord. andermal als y-Koord.
Folgerung2: Betrachtet man die {e1,...,e(m)} eingebettet als Unterraum im Rm+1, so müßten die e(i) alle formal um eine (m+1)-Koord.=0 ergänzt werden:
e'1 =(1,0,0,...,0 ,0)
e'm =(0,0,0,...,1 ,0)
e'm+1 =L({e1,...,e(m)})
L({e1,...,e(m)}) muß dann so gewählt werden, daß e'm+1 mit allen e'(i) i=1...m , rechtwinklig (skapro()=0) ist und die Länge 1 hat.
(Für beliebige Richtungen wird dies durch das sogenannte: "Schmidt'sche
Orthogonalisierungs-Verfahren" sichergestellt. )
Folgerung3: Die Notwendige Bedingung für die Festlegung einer Richtungs-Menge B={b(i)} ,i=1...m als Basis des Rm ist: Die b(i) dürfen paarweise nicht in die gleiche Richtung zeigen.
Wirkungslinien der {ei}: Durch Multipl. der e(i) mit reeller Zahl werden diese nach +-unendl. ausgedehnt. Diese Wirkungslinie:
xiei
Spezielle Richtungen im Rm sind:
e1 =(1,0,0,...,0)
e2 =(0,1,0,...,0)
e3 =(0,0,1,...,0) . . . . . em =(0,0,0,...,1)
Ein beliebiger Pkt.läßt sich dann als L() von {e(i)} i=1,...,m darstellen:
P= x1*e1 +x2*e2 +... +x(m)*e(m) , x(i) reell.
Sind alle x(i)=0 bis auf ein x(j)≠0, so verhält sich dieses x=x(j) wie eine reelle Zahl im R(1)j der Menge reeller Zahlen.
Die Multiplikation einer Richtung P mit einer reellen Zahl führt zu einer Streckung /Stauchung der Richtung:
Beispiel: P'= c*P, Norm(c*P) =c*Norm(P), also: abs(c)>1 Streckung, 1>abs(c) Stauchung.
Die skalare Multipl. der {e(i)} untereinander ergibt:
Skapro(e(i),e(j)) =0 ,∀i,j , i≠j
Skapro(e(i),e(i)) =1 ,∀i =1,...,m
Das V(e(1)***e(m)) = +1 , Maß eines m-dim norm.Eins-Würfel
Folgerung: Die Richtungen aus {e(i)} stehen paarweise senkrecht aufeinander. Sie bilden somit ein orthogonales-Eins-Richtungs-System im Rm.
Jeder Punkt P kann als Linearkombination von {e(i)} dargestellt werden:
P =(x1,x2,....,x(m))
=L({e(i)}) =x1e1 +x2e2 +...+xmem
Die e(i) werden deshalb auch als Basis-Richtungen und die {e(i)} als Basis des Rm bezeichnet
2. Unterräume des Rm :
Setzt man in der Basis {e(i)} i=1,...,m eine oder mehrere e(i) auf Null, so reduziert sich die Menge der damit dargestellten Punkte zu einer Teilmenge =Unterraum Rm-k ,k=Anzahl der auf Null gesetzen Indizes j.
Beispiel: {e1, 0, e3} , R3-1 ={x: x=(x1*e1 +x2*0 +x3*e3) ,x(i)=reell }
Hier in dem Beispiel gibt es 3 verschiedene 2-dim Unterräume:
{0, e2, e3} ,{e1, 0, e3} ,{e1, e2, 0}
Folgerung1: Jeder Rn kann als Unterraum eines Rm ,m>n aufgefaßt werden. So ist jede reelle Zahl r gleichzeitig reelle Zahl und 1-dim Unterraum R1 , wie im Beispiel des R3 einmal als x-Koord. andermal als y-Koord.
Folgerung2: Betrachtet man die {e1,...,e(m)} eingebettet als Unterraum im Rm+1, so müßten die e(i) alle formal um eine (m+1)-Koord.=0 ergänzt werden:
e'1 =(1,0,0,...,0 ,0)
e'm =(0,0,0,...,1 ,0)
e'm+1 =L({e1,...,e(m)})
L({e1,...,e(m)}) muß dann so gewählt werden, daß e'm+1 mit allen e'(i) i=1...m , rechtwinklig (skapro()=0) ist und die Länge 1 hat.
Folgerung3: Die Notwendige Bedingung für die Festlegung einer Richtungs-Menge B={b(i)} ,i=1...m als Basis des Rm ist: Die b(i) dürfen paarweise nicht in die gleiche Richtung zeigen.
Wirkungslinien der {ei}: Durch Multipl. der e(i) mit reeller Zahl werden diese nach +-unendl. ausgedehnt. Diese Wirkungslinie:
xiei
4.2 Gerade, Ebene, Dreieck:
Wird eine Richtung mit einer reellen Zahl c multipl., so verlängert sie sich, bei
c->unendl., bis ins Unendliche. Das reicht für eine Geraden-Def. aber noch nicht aus,
denn es werden die Endpunkte der Richtung mit nach unendl. bewegt und im Pkt. c=0
entsteht in der Geraden ein Loch. Dies wird durch folg. Def. behoben:
Definition Gerade:
Die Gerade durch eine vorgegebene Richtung (B-A) ist die Menge aller Punkte G mit:
G ={P: P =A+c(B-A) ,c=reell, -∞<c<∞}
Satz1: Die so def. Punktmenge ist die kürzeste Verbindung zwischen den Richtungs-Punkten.
Bemerkung: Wenn man eine Visierlinie über die Punkte A,B betrachtet, dürfen keine Punkte rts. oder lks. aus der Visierlinie herausragen. Das bedeutet für einen beliebigen aber festen Pkt.P der Strecke (B-A): d(A,B) =d(A,P) +d(P,B), die Dreiecks-Ungleichung muß "gleich" ergeben.
Beweis des Satzes1:
Bild , Anal-geo3.jpg

Ende des Beweises
Satz2: 2 Geraden schneiden sich nur in der Ebene ohne Bedingung. Ansonsten gilt:
G1: {P: P= A+c(B-A) , c=reell}
G2: {P: P= Q+c(D-C) , c=reell} ,
ist (D-C)=k*(B-A), dann G2 parallel zu G1
Definition Ebene:
Eine Ebene rotiert um eine Richtung. Durch einen 3.Punkt, ausserhalb der Richtung, wird die Ebene fixiert. Also gilt:
3 Punkte, die nicht auf einer Linie liegen, legen eindeutig eine Ebene fest. (3 Punkte in Linie werden über die Dreiecks-Ungleichung geprüft, siehe Satz1)
3 Punkte bilden 2 Richtungen in einem Pkt. aus, siehe Bild: Anal-geo4.jpg (B'-A) und (D'-A). Ebenen-Gleichung über 2 Richtungen:
Eb: {P: x(B'-A) +y(D'-A) , x,y =reell }
Fläche eines Dreiecks, bzw. PG, im Rm , die Koord. a,b,c,d im nachf. Bild liegen in der vom Dreieck (AB'D') aufgespannten Ebene.
Bild , Anal-geo4.jpg
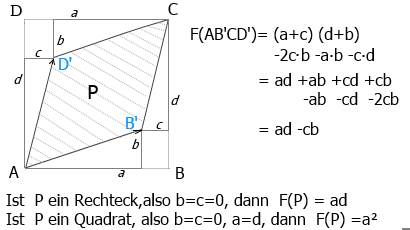
Eigenschaften des Parallelogramms:
Bild , Anal-geo5.jpg
Definition Dreieck: In der Logik der Analyt.Geometrie handelt es sich beim Dreieck nur um 3 (pos.)Zahlen a,b,c , die in Relation zueinander wie folgt stehen:
2 Seitenlängen>0 sind frei wählbar, die 3.Seitenlänge nur unter Abhängigkeit zu den beiden Ersten:
{a,b,c(a,b): (a+b)>c, c>0, a>0, b>0 }. Mit dieser Relation zwischen 3 Zahlen sind alle möglichen Dreiecke benannt!
Beispiel: a=4, c=3 frei gewählt, dann funktioniert nur noch b: 7>b>0.
Definition Gerade:
Die Gerade durch eine vorgegebene Richtung (B-A) ist die Menge aller Punkte G mit:
G ={P: P =A+c(B-A) ,c=reell, -∞<c<∞}
Satz1: Die so def. Punktmenge ist die kürzeste Verbindung zwischen den Richtungs-Punkten.
Bemerkung: Wenn man eine Visierlinie über die Punkte A,B betrachtet, dürfen keine Punkte rts. oder lks. aus der Visierlinie herausragen. Das bedeutet für einen beliebigen aber festen Pkt.P der Strecke (B-A): d(A,B) =d(A,P) +d(P,B), die Dreiecks-Ungleichung muß "gleich" ergeben.
Beweis des Satzes1:

Satz2: 2 Geraden schneiden sich nur in der Ebene ohne Bedingung. Ansonsten gilt:
G1: {P: P= A+c(B-A) , c=reell}
G2: {P: P= Q+c(D-C) , c=reell} ,
ist (D-C)=k*(B-A), dann G2 parallel zu G1
Definition Ebene:
Eine Ebene rotiert um eine Richtung. Durch einen 3.Punkt, ausserhalb der Richtung, wird die Ebene fixiert. Also gilt:
3 Punkte, die nicht auf einer Linie liegen, legen eindeutig eine Ebene fest. (3 Punkte in Linie werden über die Dreiecks-Ungleichung geprüft, siehe Satz1)
3 Punkte bilden 2 Richtungen in einem Pkt. aus, siehe Bild: Anal-geo4.jpg (B'-A) und (D'-A). Ebenen-Gleichung über 2 Richtungen:
Eb: {P: x(B'-A) +y(D'-A) , x,y =reell }
Fläche eines Dreiecks, bzw. PG, im Rm , die Koord. a,b,c,d im nachf. Bild liegen in der vom Dreieck (AB'D') aufgespannten Ebene.

Eigenschaften des Parallelogramms:

Definition Dreieck: In der Logik der Analyt.Geometrie handelt es sich beim Dreieck nur um 3 (pos.)Zahlen a,b,c , die in Relation zueinander wie folgt stehen:
2 Seitenlängen>0 sind frei wählbar, die 3.Seitenlänge nur unter Abhängigkeit zu den beiden Ersten:
{a,b,c(a,b): (a+b)>c, c>0, a>0, b>0 }. Mit dieser Relation zwischen 3 Zahlen sind alle möglichen Dreiecke benannt!
Beispiel: a=4, c=3 frei gewählt, dann funktioniert nur noch b: 7>b>0.
4.3 Geometrische Orte im Rm :
Mit geometr. Orten ist zunächst nur eine echte Teilmenge des Rm gemeint,
also Punkt oder mehrere Punkte (Punkt-Wolke). Beispiel: delta-Umgebung:
δ1 = {p,p1: d(p-p1)<r ,p,p1∈ Rm ,p1 fest, r=reell }
δ2 = {p,p1: d(pj-p1j)<r ,p,p1∈ Rm ,p1 fest, r=reell }
(δ1 =m-dim Kugel, δ2 =m-dim Intervall.)
In der ersten Stufe wollen wir mit einer variablen Gestaltung der Linearkombination versuchen, nicht nur einen Punkt o. Richtung zu beschreiben, sondern eine ganze "Schar".
Dazu werden die festen Eins-Richtungen e(i) durch ihre Wirkungslinie: x(i)*e(i) ersetzt, also durch die entspr. Koord. Achsen:
p =(a1x1,...,amxm) = a1x1e1 + ...+amxmem
Die reellen-(Variablen)-Faktoren x(i) sind jetzt frei wählbar und ergeben zunächst den gesamten Raum. Wird Rm =p({x(i)}) eingeschänkt durch z.B.: p({x(i)})=b b=reell, so erhalte ich einen kompletten Unterraum Rm-1.
Symb.: L(...,a(i)x(i),...)=b Nimmt man noch eine weitere L(...,c(i)x(i),...)=d hinzu erhält man die Schnitt-Menge der beiden Unterräume.
Beispiel1 im R3:
{L1()}: {x,y,z: x-y+z=0 ; x+y=0 }
1. Unterraum: schräge Ebene im Raum durch Gerade y=x in (x,y)-Ebene(Projektion des Raumes)
2. Unterraum: senkrechte Ebene im Raum, parallel zur z-Achse, durch Gerade y=x in (x,y)-Ebene(Projektion des Raumes)
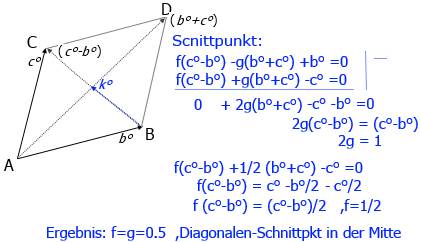
Ergebnis: Die Schnittmenge 2-er Ebenen, die nicht parallel sind, ist eine Gerade im Raum, die die (x,y)-Ebene im Punkt 0 durchdringt, also ein R3-2 -Unterraum =Linienzug im Raum, hier Gerade, 2.Pkt.=(0.5, -0.5, 1).
Beispiel2 im R3:
{L2()}: {x,y,z: x-y=1 ; x+y=2 }
Ergebnis: Die Schnittmenge ist eine senkrecht zur (x,y)-Ebene stehende Gerade im Raum, die durch den Pkt.(1.5 ,0.5, 0) geht.
Bild , Anal-geo6.jpg
Koordinaten-Systeme:
Die Multipl. der e(i) mit einer reellen Zahl heißt Wirkungslinie durch die Eins-Richtung von -unendl. bis +unendl.
Def.: Die Menge aller Wirkungslinien {x(i)*e(i)} heißt Koord.-System des Rm mit folg.Eigenschaften:
Skapro(e(i),e(i+1) =0
V(e(i)*e(i+1) =+1 , i=1,...,m-1
Die 1. Eigenschaft sichert rechtwinkligkeit,
Die 2. Eigenschaft sichert pos. Orientierung.
Volumen-Produkt 2-er Richt.:
x=(x(1,...,x(m)) ,y=(y(1,...,y(m)), dann ist:
V(x*y)= ...x(i)y(j)*e(i)e(j)... ,1..i,j..m
wobei gilt: alle e(i)*e(i)=0 ,(wegen parall.)
e(i)*e(j) =-1, i≠j ,i>j sonst =1
d.h, m(m-1) mal +1, m(m-1) mal -1
Beispiel:
(3e(1) +2e(2) -6e(3)*(1e(1) -4e(2) +5e(3))
= 3e(1)² +8e(2)² -30e(3)²
-12e(1)e(2) +15e(1)e(3) +2e(2)e(1)
+12e(2)e(3) -6e(3)e(1) +24e(3)e(2)
-----------------------
= (-12 -2)*1 +(15 +6)*1 +(10 -24)*1
-14 +21 -14 =-7 , hat geometr. keine Bedeutung
Die Fläche der Projektion in e(1)e(2) Unterraum ist:
(3 *- 4) -(2 * 1) =-14
geometr. Orte im Rm sind Punkte, Punktfolgen oder allg. Punkt-Mengen, die durch eine Anzahl vvon Bedingungen {f(i)=b(i)}, hier in der 1.Stufe der Analyt.Geometrie linear.Kombin. {L((i)=b(i)}, eingeschränkt werden.
Damit etwas Vernünftiges (Punkt o. Mengen) dabei herauskommt, müssen die L(i)=b(i) bestimmten Anforderungen genügen.
Zur Untersuchung wird äquivalent die Lösungs-Menge eines zugehöriges lin. Gleich.System herangezogen.
(δ1 =m-dim Kugel, δ2 =m-dim Intervall.)
In der ersten Stufe wollen wir mit einer variablen Gestaltung der Linearkombination versuchen, nicht nur einen Punkt o. Richtung zu beschreiben, sondern eine ganze "Schar".
Dazu werden die festen Eins-Richtungen e(i) durch ihre Wirkungslinie: x(i)*e(i) ersetzt, also durch die entspr. Koord. Achsen:
p =(a1x1,...,amxm) = a1x1e1 + ...+amxmem
Die reellen-(Variablen)-Faktoren x(i) sind jetzt frei wählbar und ergeben zunächst den gesamten Raum. Wird Rm =p({x(i)}) eingeschänkt durch z.B.: p({x(i)})=b b=reell, so erhalte ich einen kompletten Unterraum Rm-1.
Symb.: L(...,a(i)x(i),...)=b Nimmt man noch eine weitere L(...,c(i)x(i),...)=d hinzu erhält man die Schnitt-Menge der beiden Unterräume.
Beispiel1 im R3:
{L1()}: {x,y,z: x-y+z=0 ; x+y=0 }
1. Unterraum: schräge Ebene im Raum durch Gerade y=x in (x,y)-Ebene(Projektion des Raumes)
2. Unterraum: senkrechte Ebene im Raum, parallel zur z-Achse, durch Gerade y=x in (x,y)-Ebene(Projektion des Raumes)
Ergebnis: Die Schnittmenge 2-er Ebenen, die nicht parallel sind, ist eine Gerade im Raum, die die (x,y)-Ebene im Punkt 0 durchdringt, also ein R3-2 -Unterraum =Linienzug im Raum, hier Gerade, 2.Pkt.=(0.5, -0.5, 1).
Beispiel2 im R3:
{L2()}: {x,y,z: x-y=1 ; x+y=2 }
Ergebnis: Die Schnittmenge ist eine senkrecht zur (x,y)-Ebene stehende Gerade im Raum, die durch den Pkt.(1.5 ,0.5, 0) geht.

Koordinaten-Systeme:
Die Multipl. der e(i) mit einer reellen Zahl heißt Wirkungslinie durch die Eins-Richtung von -unendl. bis +unendl.
Def.: Die Menge aller Wirkungslinien {x(i)*e(i)} heißt Koord.-System des Rm mit folg.Eigenschaften:
Skapro(e(i),e(i+1) =0
V(e(i)*e(i+1) =+1 , i=1,...,m-1
Die 1. Eigenschaft sichert rechtwinkligkeit,
Die 2. Eigenschaft sichert pos. Orientierung.
Volumen-Produkt 2-er Richt.:
x=(x(1,...,x(m)) ,y=(y(1,...,y(m)), dann ist:
V(x*y)= ...x(i)y(j)*e(i)e(j)... ,1..i,j..m
wobei gilt: alle e(i)*e(i)=0 ,(wegen parall.)
e(i)*e(j) =-1, i≠j ,i>j sonst =1
d.h, m(m-1) mal +1, m(m-1) mal -1
Beispiel:
(3e(1) +2e(2) -6e(3)*(1e(1) -4e(2) +5e(3))
= 3e(1)² +8e(2)² -30e(3)²
-12e(1)e(2) +15e(1)e(3) +2e(2)e(1)
+12e(2)e(3) -6e(3)e(1) +24e(3)e(2)
-----------------------
= (-12 -2)*1 +(15 +6)*1 +(10 -24)*1
-14 +21 -14 =-7
Die Fläche der Projektion in e(1)e(2) Unterraum ist:
(3 *- 4) -(2 * 1) =-14
geometr. Orte im Rm sind Punkte, Punktfolgen oder allg. Punkt-Mengen, die durch eine Anzahl vvon Bedingungen {f(i)=b(i)}, hier in der 1.Stufe der Analyt.Geometrie linear.Kombin. {L((i)=b(i)}, eingeschränkt werden.
Damit etwas Vernünftiges (Punkt o. Mengen) dabei herauskommt, müssen die L(i)=b(i) bestimmten Anforderungen genügen.
Zur Untersuchung wird äquivalent die Lösungs-Menge eines zugehöriges lin. Gleich.System herangezogen.
4.4 Lineare Gleich. Systeme:
Allg. Vektor-Raum:
Die Elemente eines Vektorraumes brauchen zunächst nicht def. werden, sondern nur ihre Verknüpfungs-Axiomatik:
1. Add.:wie Richtungs-Axiomatik Rm
1. a+b=c (add. von Elementen)
2. (a+b) = (b+a)(kommutativ)
3. (a+b)+c =a+(b+c)(assoziativ)
4. a+x=b(Umkehrung zu x=b-a)
2. Multi:, f,g =reell
1. a*1=a(Eins-Element)
2. f(g*a)=(f*g)*a(assoziativ)
3. (f+g)*a=f*a +g*a(distributiv)
4. f(a+b)=f*a +f*b(distributiv)
Folgerung1:
Aus Umkehrung ergibt sich die Existenz eine Null-Elementes: a+Null=a und die Existenz einer Umkehr-Operation: a-b=c
Folgerung2:
Jeder Vektor läßt sich als Lin.Komb. anderer Vektoren darstellen:
a= r(1)*b(1) + ... + r(m)*b(m), auch Null:
z.B.: 3a -2b +5c =Null(a=2, b=1, c=4/5)
Folgerung3: Die (x1,...,x(m) ) ,x(i)=reell , sind demnach ein Vektorraum.
z.B. ist x=(b(1)-a(1),...,b(m)-a(m)) Lösung der Gleichung: a+x=b.
Satz1:
Der Vektorraum R² und die Gaußsche-Zahlen-Ebene sind über die Koord. Darstellung zu jeder Zeit äquivalent =Repräsentant der Ebene:
z1=x1+i*y1 =(x1,y1), Konstante
z=x+i*y =(x,y), Variable
A(z) =(Ax(x) , Ay(y)), Ausdruck
F(z) =(F1(x) , F2(y)), Funktion
Spez. Ausdruck 'Lin.Komb.' im Vektorraum Rm:
L(a(1),..a(n)=b bedeutet: Ich suche n-reelle Zahlen xi, so daß die Gleichung: a(1)*x(1)+...+a(n)*x(n)=b gilt. In Koord. Schreibweise ergibt das dann m-Einzel-Gleicheungen.
Also: die L() im Vektorraum ist mit dem Operator: "Lin.Gl.System zur Beschreibung /Bestimmung von n-reell.Zahlen" äquivalent.
Satz2: Jedes Element ist gleichzeitig L({}e(i)=b der Eins-Basis-Vektoren:
e(i)=(0,...,1i,...,0) , b=(b(1),...,b(m))
Nach Axiom 2.2 gilt für jedes j: b(j)= e(j)*b(j)
Nach Axiom 1.1 können alls b(j) aufadd. werden:
e(1)*b(1) +... + e(m)*b(m) , => Lin.Gl.System:
e(1,1)*x(1) +... + e(1,m)*b(m) =b(1)
. . . . .
0*x(1)... e(i,i)*b(i)...0*x(m) =b(i) , e(i,i)=1
. . . . .
e(m,1)*x(1) +... + e(m,m)*b(m) =b(m)
Man erkennt sofort, daß System mit x=(b1,...,b(m)) eindeutig lösbar ist.
Satz3: Ein Vektor-System {A(i)}, bei dem die A(i) aus {e(j)} gebildet wurden, ist linear unabhängig, wenn L(A(1),..,A(m))=0 eindeutig nur mit x()=(0,...,0) lösbar ist.
Beweis:
Je 2 Elemente können wie folgt dargestellt werden:
a=(x1*a1,...x(m)*a(m)) , b=(x1'*a1,...x(m)'*a(m))
j: ...(x(j)-x(j)')*a(j)=0 ... nur, wenn die a(j)=0 sind.
d.h., kein Vektor darf ein Vielfaches eines anderen sein.
Satz4: Ein unabhängiges Vektor-System {A(i)} im Rm, muß aus genau m-Vektoren bestehen.
Beweis:
Es seien nur m-1 A(i) vorhanden und b=x(1)*a(1)+...+x(m-1)*a(m-1), dann ist:
A1+...+A(m-1) -b =Null eine Lin.Komb. im Rm ,mit Lösungsvektor =(x(1),...,x(m-1),-1) ungleich Null. Ich komm also mit m-1 Vektoren nicht in den gesamten Raum hiniein.
Satz5: Eine Menge von m Vektoren ist linear unabhängig und damit Basis im Rm, wenn die Gleichung x(1)a1+...x(m)a(m)=Null nur 1 triviale Lösung (x1=0,...,x(m)=0) besitzt.
Gegen-Beispiel: a=(2,3) und b=(-3, -9/2) sind keine Basis im R², da:
2*x1 -3*x2 =0
-3*x1 -(9/2)x2 =0 ,=> x1= -(3/2)x2
mit z.B. (-3,2) lösbar ist.
Folgerung4: Die lin.Komb. von Basis-Vektoren führen nicht aus dem Raum der Basis-Vektoren hinaus. Man sagt auch: Die {b(i)} ,i=1...m spannen den Raum, hier Rm, auf.
Definition Unterraum: Eine Menge A von Vektoren heißt 'Unterraum' des Rm, wenn:
1. Aus a,b∈A folgt: (a+b)∈A
2. Aus a∈A und r=reell folgt: r*a∈A
Satz6: Die Lösungsmenge inhomogener Gl.Systeme ist kein Unterraum des Rm, weil der Null-Vektor keine Lösung von
a(1)*x(1)+...+a(m)*x(m)=b sein kann, wenn b≠Null.
Die Elemente eines Vektorraumes brauchen zunächst nicht def. werden, sondern nur ihre Verknüpfungs-Axiomatik:
1. Add.:
2. (a+b) = (b+a)
3. (a+b)+c =a+(b+c)
4. a+x=b
2. Multi:
1. a*1=a
2. f(g*a)=(f*g)*a
3. (f+g)*a=f*a +g*a
4. f(a+b)=f*a +f*b
Folgerung1:
Aus Umkehrung ergibt sich die Existenz eine Null-Elementes: a+Null=a und die Existenz einer Umkehr-Operation: a-b=c
Folgerung2:
Jeder Vektor läßt sich als Lin.Komb. anderer Vektoren darstellen:
a= r(1)*b(1) + ... + r(m)*b(m), auch Null:
z.B.: 3a -2b +5c =Null
Folgerung3: Die (x1,...,x(m) ) ,x(i)=reell , sind demnach ein Vektorraum.
z.B. ist x=(b(1)-a(1),...,b(m)-a(m)) Lösung der Gleichung: a+x=b.
Satz1:
Der Vektorraum R² und die Gaußsche-Zahlen-Ebene sind über die Koord. Darstellung zu jeder Zeit äquivalent =Repräsentant der Ebene:
z1=x1+i*y1 =(x1,y1)
z=x+i*y =(x,y)
A(z) =(Ax(x) , Ay(y))
F(z) =(F1(x) , F2(y))
Spez. Ausdruck 'Lin.Komb.' im Vektorraum Rm:
L(a(1),..a(n)=b bedeutet: Ich suche n-reelle Zahlen xi, so daß die Gleichung: a(1)*x(1)+...+a(n)*x(n)=b gilt. In Koord. Schreibweise ergibt das dann m-Einzel-Gleicheungen.
Also: die L() im Vektorraum ist mit dem Operator: "Lin.Gl.System zur Beschreibung /Bestimmung von n-reell.Zahlen" äquivalent.
Bemerkung:
Die Menge L(a)=b kann man selbst als Topologischer Raum auffassen, mit L() als einzelnem Element. Die Lösung lin.Gl.Systeme ist dann gleichwertig einer konvergenten Folge {Li()}->L(), wobei hier die (x1..x(m)) des L() als Lösungs-Vektor betrachtet wird.
Über entspr. Fixpunkt-Sätze wird die Existenz solcher Grenzwerte (Lösungen) nachgewiesen. (kontrahierende Operatoren)
Die Menge L(a)=b kann man selbst als Topologischer Raum auffassen, mit L() als einzelnem Element. Die Lösung lin.Gl.Systeme ist dann gleichwertig einer konvergenten Folge {Li()}->L(), wobei hier die (x1..x(m)) des L() als Lösungs-Vektor betrachtet wird.
Über entspr. Fixpunkt-Sätze wird die Existenz solcher Grenzwerte (Lösungen) nachgewiesen. (kontrahierende Operatoren)
Satz2: Jedes Element ist gleichzeitig L({}e(i)=b der Eins-Basis-Vektoren:
e(i)=(0,...,1i,...,0) , b=(b(1),...,b(m))
Nach Axiom 2.2 gilt für jedes j: b(j)= e(j)*b(j)
Nach Axiom 1.1 können alls b(j) aufadd. werden:
e(1)*b(1) +... + e(m)*b(m) , => Lin.Gl.System:
e(1,1)*x(1) +... + e(1,m)*b(m) =b(1)
. . . . .
0*x(1)... e(i,i)*b(i)...0*x(m) =b(i) , e(i,i)=1
. . . . .
e(m,1)*x(1) +... + e(m,m)*b(m) =b(m)
Man erkennt sofort, daß System mit x=(b1,...,b(m)) eindeutig lösbar ist.
Satz3: Ein Vektor-System {A(i)}, bei dem die A(i) aus {e(j)} gebildet wurden, ist linear unabhängig, wenn L(A(1),..,A(m))=0 eindeutig nur mit x()=(0,...,0) lösbar ist.
Beweis:
Je 2 Elemente können wie folgt dargestellt werden:
a=(x1*a1,...x(m)*a(m)) , b=(x1'*a1,...x(m)'*a(m))
j: ...(x(j)-x(j)')*a(j)=0 ... nur, wenn die a(j)=0 sind.
d.h., kein Vektor darf ein Vielfaches eines anderen sein.
Satz4: Ein unabhängiges Vektor-System {A(i)} im Rm, muß aus genau m-Vektoren bestehen.
Beweis:
Es seien nur m-1 A(i) vorhanden und b=x(1)*a(1)+...+x(m-1)*a(m-1), dann ist:
A1+...+A(m-1) -b =Null eine Lin.Komb. im Rm ,mit Lösungsvektor =(x(1),...,x(m-1),-1) ungleich Null. Ich komm also mit m-1 Vektoren nicht in den gesamten Raum hiniein.
Satz5: Eine Menge von m Vektoren ist linear unabhängig und damit Basis im Rm, wenn die Gleichung x(1)a1+...x(m)a(m)=Null nur 1 triviale Lösung (x1=0,...,x(m)=0) besitzt.
Gegen-Beispiel: a=(2,3) und b=(-3, -9/2) sind keine Basis im R², da:
2*x1 -3*x2 =0
-3*x1 -(9/2)x2 =0 ,=> x1= -(3/2)x2
mit z.B. (-3,2) lösbar ist.
Folgerung4: Die lin.Komb. von Basis-Vektoren führen nicht aus dem Raum der Basis-Vektoren hinaus. Man sagt auch: Die {b(i)} ,i=1...m spannen den Raum, hier Rm, auf.
Definition Unterraum: Eine Menge A von Vektoren heißt 'Unterraum' des Rm, wenn:
1. Aus a,b∈A folgt: (a+b)∈A
2. Aus a∈A und r=reell folgt: r*a∈A
Satz6: Die Lösungsmenge inhomogener Gl.Systeme ist kein Unterraum des Rm, weil der Null-Vektor keine Lösung von
a(1)*x(1)+...+a(m)*x(m)=b sein kann, wenn b≠Null.
4.5 Der Lösungsraum lin.Gl.Systeme:
Definition Skapro() o. inneres Produkt:
1. Die m-Tupel reeller Zahlen heißen Zeilen-Vektoren
2. Sind a,x Zeilen-Vektoren, so ist x T Spalten-Vektor und skapro(a,x)=ax T =a(1)x(1)+...+a(m)*x(m) =reelle Zahl.
3. (a+b)T = aT+bT gilt für Zeilen/Spalten-Vektoren
4. (r*a)T = r*aT
5. skapro(j=1..n)(c(j)a(j)) * skapro(k=1..m)(d(k)x(k))
= Sum(j,k)(c(j)*d(k)*a(j)*x(k))
Beispiel: (3x1 +5x2) * (2y1 +3y2 +6y3)
= 6x1y1 +9x1y2 +18x1y3 +10x2y1 +15x2y2 +30x2y3
Folgerung: Ist aaT=0 ,folgt a=0
Definition homogen.lin.Gl.System:
M=(a1...a(m))T = a1...a(m) als Spalten-Vektor:
(a(1,1) . . . a(1,m) )
(a(2,1) . . . a(2,m) )
. . . . . . . .
(a(n,1) . . . a(n,m) )
M so aufgeschrieben heißt Matrix und M*x=0 homogen.lin.Gl.System:
a(1,1)x1 + ... +a(1,m)x(m) =0
a(2,1)x1 + ... +a(2,m)x(m) =0
. . . . . . . .
a(n,1)x1 + ... +a(n,m)x(m) =0
Der Lösungsraum x=(x1...x(m)) hat die Dim m-n, wenn m die Anzahl lin.unabhäng. Vektoren a(i) ist. Fallunterscheidung:
1. m-n<0 , dann Widerspruch
2. m-n=0 , dann Null-Vektor, eindeutige Lösung
3. m-n>0 , dann (m-n)-dim Lösungsraum
Es gilt allg. bei m-n>0:
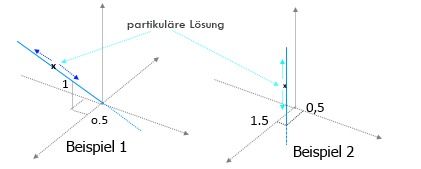
x° =Lösung M*x°=b, und á =Lösung von M*x=0
dann folgt aus M*x°+M*á =b , M(x°+á)=b
Dies bedeutet:
Satz1:
Existiert eine partikuläre Lösung x° von M*x=b, dann gehört auch der gesamte Lösungsraum á von M*x=0 zu den Lösungen von M*x=b, also x°+á.
Satz2:
Ein inhom.lin.Gl.System M*x=b ist genau dann lösbar, wenn die Anzahl lin.unabhäng. Zeilen/Spalten-Vektoren von M mit der der erweit.Koeff.Matrix übereinstimmt.
Dim(M) = Dim(M,b)
Lösungsweg:
Ein Lösungsweg, der immer funktioniert ist das Gaussche Eliminierungs-Verfahren:
Spalten von lks.->rts abarbeiten.
Ergebnis ist Matrix in weitestgehend Dreieckform. Dann die Werte rückwärt wieder einsetzen. Bei einer (m,m) Matrix wären das ca. 4m² Gleitkomma-Operationen. Für schnelle Rechner kein Problem.
1. Die m-Tupel reeller Zahlen heißen Zeilen-Vektoren
2. Sind a,x Zeilen-Vektoren, so ist x T Spalten-Vektor und skapro(a,x)=ax T =a(1)x(1)+...+a(m)*x(m) =reelle Zahl.
3. (a+b)T = aT+bT
4. (r*a)T = r*aT
5. skapro(j=1..n)(c(j)a(j)) * skapro(k=1..m)(d(k)x(k))
= Sum(j,k)(c(j)*d(k)*a(j)*x(k))
Beispiel: (3x1 +5x2) * (2y1 +3y2 +6y3)
= 6x1y1 +9x1y2 +18x1y3 +10x2y1 +15x2y2 +30x2y3
Folgerung: Ist aaT=0 ,folgt a=0
Definition homogen.lin.Gl.System:
M=(a1...a(m))T = a1...a(m) als Spalten-Vektor:
(a(1,1) . . . a(1,m) )
(a(2,1) . . . a(2,m) )
. . . . . . . .
(a(n,1) . . . a(n,m) )
M so aufgeschrieben heißt Matrix und M*x=0 homogen.lin.Gl.System:
a(1,1)x1 + ... +a(1,m)x(m) =0
a(2,1)x1 + ... +a(2,m)x(m) =0
. . . . . . . .
a(n,1)x1 + ... +a(n,m)x(m) =0
Der Lösungsraum x=(x1...x(m)) hat die Dim m-n, wenn m die Anzahl lin.unabhäng. Vektoren a(i) ist. Fallunterscheidung:
1. m-n<0 , dann Widerspruch
2. m-n=0 , dann Null-Vektor, eindeutige Lösung
3. m-n>0 , dann (m-n)-dim Lösungsraum
Es gilt allg. bei m-n>0:
x° =Lösung M*x°=b, und á =Lösung von M*x=0
dann folgt aus M*x°+M*á =b , M(x°+á)=b
Dies bedeutet:
Satz1:
Existiert eine partikuläre Lösung x° von M*x=b, dann gehört auch der gesamte Lösungsraum á von M*x=0 zu den Lösungen von M*x=b, also x°+á.
Satz2:
Ein inhom.lin.Gl.System M*x=b ist genau dann lösbar, wenn die Anzahl lin.unabhäng. Zeilen/Spalten-Vektoren von M mit der der erweit.Koeff.Matrix übereinstimmt.
Dim(M) = Dim(M,b)
Lösungsweg:
Ein Lösungsweg, der immer funktioniert ist das Gaussche Eliminierungs-Verfahren:
Spalten von lks.->rts abarbeiten.
Ergebnis ist Matrix in weitestgehend Dreieckform. Dann die Werte rückwärt wieder einsetzen. Bei einer (m,m) Matrix wären das ca. 4m² Gleitkomma-Operationen. Für schnelle Rechner kein Problem.
Beispiel für Lösungs-Menge:
3x1 +1x2 +2x3 =6 -6/3
6x1 +4x2 -x3 =3 +
-----------------
3x1 +1x2 +2x3 = 6 (Gl.1)
0 + 2x2 -5x3 =-9
-----------------
2x2 = -9 +5x3 (Wählen x3 =9/5)
==> x2 =0 (x2 ,x3 Einsetz. Gl.1)
==> 3x1 +0 +2(9/5) = 6
==> x1 = 6 -18/5)/3 = 2-6/5
==> x1 =4/5
x°=(4/5 ,0 ,9/5 ) partikuläre Lösung
Lösungsraum: 1-dim
x° +á :
=( 4/5-3/2x , 5/2x , 9/5+x )
3x1 +1x2 +2x3 =0 -6/3
6x1 +4x2 -x3 = 0 +
-----------------
3x1 +1x2 +2x3 =0 (Gl.1)
0 (-6/3 +4)x2 +(-12/3 +1)x3 =0
==> (-6/3 +12/3)x2 = 15/3x3
==> 2x2 = 5x3 (in Gl.1 einsetzen)
--------------------
3x1 +5/2x3 +2x3 =0 ==> 3x1 +9/2x3 =0
==> x1= -3/2x3 (x3 =x setzen)
á =(-3/2x ,5/2x ,x) variabl.Lösung
Folgendes Beispiel ist ein typisches LGL-System aus der
Knotenpunkt-Analyse der Elektrotechnik mit schwach-besetzter Matrix und Det.≠0
Progamm zur Lösung allg. LGL-Systeme (n,m):
4.6 Koordinaten-Transformationen:
Aus der Axiomatik des "Raumes mit Skalar-Produkt" heraus hatten wir
als natürliche Koord. Achsen die {x(i)*e(i)} , i=1...m ,e(i)=(0...,1,...0)
erkannt. Wenn nichts anderes festgelegt, werden immer diese Koord. unterstellt.
Eigenschaften der e(i):
1. Skapro(e(i),e(j) =1 (i=j), =0 (i≠j)
2. V(e(i),e(j) =0 (i=j), =1 (i≠j) V() ist die Fläche zwischen den e(i), wenn Rm=2, bei Rm>2 allg. m-dim Volumen (Spat o.ä).
V(e1...em) = Vol.eines m-dim Eins-Würfels=1
3. M=Matrix, M({e(i)}):
(1 0 . . . .0)
(0 1 . . . .0)
. . . . . .
(0 0 . . . .1) , Diese Form einer Matrix ist die Einfachste im Rm , hat das Vol.1 , die Achsen sind alle rechtwinklig zueinander, und die Orientierung ist positiv =1. Was heißt das:
Ich kann die Achsen von Index 1 an beginnend mit dem kleinsten Winkel, hier 90°, in die nächst Folgende Achse drehen.
Alle anderen Achsen-System, bei denen das ab irgendeinem Index an abweicht, werden mit Faktor (-1) belegt, Am Ende ergibt (-1)k, k=Anz. Abweichungen, die Orientierung des Systems + oder -.
3. Sind b(i) linear unabhängig,d.h. Sum(b(i))=Null nur wenn alle
b(i)=0 sind , dann ist {b'(i)}={b(i)/abs(b(i))} ebenfalls ein System von
Eins-Richtungen und das abs(V(b1....b(m))) ist ≤V(e1...e(m))=1, "gleich" nur,
wenn die b(i) sich durch geeignete Drehungen mit den e(j) zur Deckung bringen
lassen können.
Da die b(i) selbst Lin.Komb von e(i) sind, siehe: Satz2 Abschnitt 4.4,
drückt V() das Verhältnis zweier verschiedener Volumen, die von 2 Richtungs-Systemen aufgespannt werden, aus.
Sei M=Matrix der zug.Lin.Komb. von b(i):
(a11 a21 . . . am1)
(a21 a22 . . . am2)
( . . . . . . )
(am1 am2 . . . amm) , dann gilt:
V(M) =V({b(i)}) /V({e(i)})
Seien C={c(i)} Lin.Komb. von B={b(i)} so folgt aus:
V(c(i)) /V(e(i)) und V({b(i)}) /V({e(i)}):
1 =V(e(i)) /V(e(i)) =V(c(i)) /V(b(i))
Dieser Ausdruck besagt, daß die Systeme b(i) und c(i) zueinander invers sind.
Betrachtet man die Lin.Komb. als eigenständige Transformation in der Menge aller (Lin.)-Transformationen,siehe: Bemerkung Abschnitt 4.4 ,
so kann man schreiben B(C({e(i)})) =Eins() oder B*C-1=Eins() weil
auch gilt:
C*[B*C-1]=c*[Eins()] =C , wegen: C=C(B)
==> C(B(C-1))) = C(B) ,wegen: B*C-1=Eins()
==> C(Eins()) = C(B), d.h. C,B sind gegenseitig invers.
Beispiel:
Bild , Anal-geo7.jpg
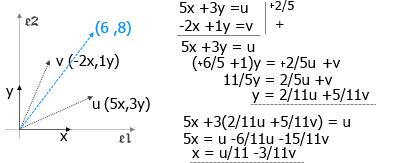
Im Beispiel gibt es 2 Systeme A,B bestehend aus Menge von 4 Richtungen (y,v,u,x):
A={x,y} , B={u,v}
A= Matrix(x(1,0),y(0,1)) , B= Matrix(u(1,0),v(0,1))
Die Systeme, respektive die Matrizen, können gegenseitig umgerechnet werden, durch 2 lin.Gl.Systeme:
(Gl.1)
( 5x 3y) = 1u
(-2x 1y) = 1v oder umgekehrt:
(Gl.2)
(1/11u -3/11v) = 1x
( 2/11u 5/11v) = 1y
Laut Matrix-Def. (siehe oben) ist:
A= ( 5 3)
(-2 1)
B= (1/11 -3/11)
( 2/11 5/11)
Für diese spez.Matrizen =Transform. kann man folg. Aussagen machen:
1. A(B) ergibt A*B =Skapro(i-Zeile_B,j-Spalte_A):
(1,1): 5*1/11 + 3*2/11 =1
(2,1): -2* 1/11 + 1*2/11 =0
(1,2): 5*-3/11 + 3*5/11 =0
(2,2): -2*(-3)/11 + 1*5/11 =1
Ergebnis= (e1,e2) und Det(e1,e2) =1, die u,v haben gleiche Orientierung wie x,y, und x,y sind gleiche Richtung wie e1,e2
2. A,B sind invers zueinander
3. A(B) =A*B =B*A =B(A) , die Reihenfolge der Transform. spielt keine Rolle.
Für allg. Matrizen =Transform. gilt aber:
A(B) = (BTAT)T , Matrizen-Multipl. ist nicht kommutativ.
Siehe Bild: Anal-geo7.jpg:
Der Pkt.(6,8) in Dim[x,y] hat die Koord.(2,2) in Dim[u,v]:
6*(1/11u -3/11v) , 8*(2/11u +5/11v) ->(2u ,2v) =(2,2)
Der Pkt.(2,2) in Dim[u,v] hat die Koord.(2,2) in Dim[x,y]:
2*(5x +3y) , 2(-2x +y) ->(6x ,8y) =(6,8)
Fazit: Der gleiche Punkt /Richtung im Raum hat bezüglich seiner Länge, Volumen, wenn mehrere Richtungen, in den unterschiedlichen Bezugs-Systemen (Koord.Achsen) zwar verschiedene Werte, die sich aber problemlos ineinander umrechnen lassen können.
Beispiel: Kreisscheibe(r) hat Fläche pi*r² in Dim[dxdy] = r²/2*Bog(360°) in Dim[drdφ] .
Beispiel: allg. Koord.Transformation im R2 , R3
Bild , Lin_Gl_2-3dim.jpg

Allg. Determinanten Definition 'D':
Bild , Det_def.jpg

Eigenschaften der e(i):
1. Skapro(e(i),e(j) =1 (i=j), =0 (i≠j)
2. V(e(i),e(j) =0 (i=j), =1 (i≠j) V() ist die Fläche zwischen den e(i), wenn Rm=2, bei Rm>2 allg. m-dim Volumen (Spat o.ä).
V(e1...em) = Vol.eines m-dim Eins-Würfels=1
3. M=Matrix, M({e(i)}):
(1 0 . . . .0)
(0 1 . . . .0)
. . . . . .
(0 0 . . . .1) , Diese Form einer Matrix ist die Einfachste im Rm , hat das Vol.1 , die Achsen sind alle rechtwinklig zueinander, und die Orientierung ist positiv =1. Was heißt das:
Ich kann die Achsen von Index 1 an beginnend mit dem kleinsten Winkel, hier 90°, in die nächst Folgende Achse drehen.
Alle anderen Achsen-System, bei denen das ab irgendeinem Index an abweicht, werden mit Faktor (-1) belegt, Am Ende ergibt (-1)k, k=Anz. Abweichungen, die Orientierung des Systems + oder -.
3. Sind b(i) linear unabhängig,
Da die b(i) selbst Lin.Komb von e(i) sind, siehe: Satz2 Abschnitt 4.4,
drückt V() das Verhältnis zweier verschiedener Volumen, die von 2 Richtungs-Systemen aufgespannt werden, aus.
Sei M=Matrix der zug.Lin.Komb. von b(i):
(a11 a21 . . . am1)
(a21 a22 . . . am2)
( . . . . . . )
(am1 am2 . . . amm) , dann gilt:
V(M) =V({b(i)}) /V({e(i)})
Seien C={c(i)} Lin.Komb. von B={b(i)} so folgt aus:
V(c(i)) /V(e(i)) und V({b(i)}) /V({e(i)}):
1 =V(e(i)) /V(e(i)) =V(c(i)) /V(b(i))
Dieser Ausdruck besagt, daß die Systeme b(i) und c(i) zueinander invers sind.
Betrachtet man die Lin.Komb. als eigenständige Transformation in der Menge aller (Lin.)-Transformationen,
C*[B*C-1]=c*[Eins()] =C , wegen: C=C(B)
==> C(B(C-1))) = C(B) ,
==> C(Eins()) = C(B), d.h. C,B sind gegenseitig invers.
Beispiel:
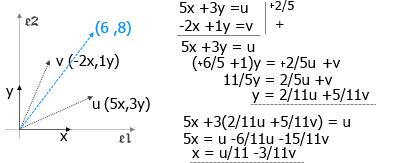
Im Beispiel gibt es 2 Systeme A,B bestehend aus Menge von 4 Richtungen (y,v,u,x):
A={x,y} , B={u,v}
A= Matrix(x(1,0),y(0,1)) , B= Matrix(u(1,0),v(0,1))
Die Systeme, respektive die Matrizen, können gegenseitig umgerechnet werden, durch 2 lin.Gl.Systeme:
(Gl.1)
( 5x 3y) = 1u
(-2x 1y) = 1v
(Gl.2)
(1/11u -3/11v) = 1x
( 2/11u 5/11v) = 1y
Laut Matrix-Def. (siehe oben) ist:
(-2 1)
B= (1/11 -3/11)
( 2/11 5/11)
1. A(B) ergibt A*B =Skapro(i-Zeile_B,j-Spalte_A):
(1,1): 5*1/11 + 3*2/11 =1
(2,1): -2* 1/11 + 1*2/11 =0
(1,2): 5*-3/11 + 3*5/11 =0
(2,2): -2*(-3)/11 + 1*5/11 =1
Ergebnis= (e1,e2) und Det(e1,e2) =1, die u,v haben gleiche Orientierung wie x,y, und x,y sind gleiche Richtung wie e1,e2
2. A,B sind invers zueinander
3. A(B) =A*B =B*A =B(A) , die Reihenfolge der Transform. spielt keine Rolle.
Für allg. Matrizen =Transform. gilt aber:
A(B) = (BTAT)T , Matrizen-Multipl. ist nicht kommutativ.
Siehe Bild: Anal-geo7.jpg:
Der Pkt.(6,8) in Dim[x,y] hat die Koord.(2,2) in Dim[u,v]:
6*(1/11u -3/11v) , 8*(2/11u +5/11v) ->(2u ,2v) =(2,2)
Der Pkt.(2,2) in Dim[u,v] hat die Koord.(2,2) in Dim[x,y]:
2*(5x +3y) , 2(-2x +y) ->(6x ,8y) =(6,8)
Fazit: Der gleiche Punkt /Richtung im Raum hat bezüglich seiner Länge, Volumen, wenn mehrere Richtungen, in den unterschiedlichen Bezugs-Systemen (Koord.Achsen) zwar verschiedene Werte, die sich aber problemlos ineinander umrechnen lassen können.
Beispiel: Kreisscheibe(r) hat Fläche pi*r² in Dim[dxdy] = r²/2*Bog(360°) in Dim[drdφ] .
Beispiel: allg. Koord.Transformation im R2 , R3

Allg. Determinanten Definition 'D':

4.7 Geometr.Deutung der Lin.Komb():
Nach des Axiomen des Eukl.Raumes ist jede Lin.Komb. von Punkten, wiederum
Element des Raumes, also Punkt. (siehe Abschnitt 4.4)
Also gilt auch umgekehrt: B=(b1,...,b(m)) =L(P1,...,P(n)):
Bild , Anal-geo9.jpg
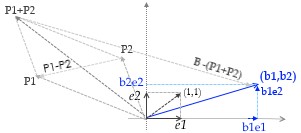
(P1+P2)+(B-(P1+P2) oder P2+(B-P2) etc.
Koord.Vergleich:
P1=(a11,a12), P2=(a21,a22), z.B.:
(P1+P2)+(B-(P1+P2) =
=> 1.Koord.: a11+a11 +b1-(a11+a21) =b1
2.Koord.: a12+a12 +b1-(a12+a22) =b2
= (b1,b2) =B
Schlussfolgerung: Um zu seinem Ziel zu gelangen, kann man viele Umwege gehen, oder direkt sein Ziel auf kürzestem Weg ansteuern!
Die Lösung ist, die Normierung aller Wege (=Lin.Komb.), die zu B führen, in dem man als Ausgangspunkt das Eins-Element des Raumes, hier (e1,e2)=(1,1), wählt:
b1*e1 +b2*e2 +....+b(m)*e(m) =B(b1,b2,..)
Def.: Die Darstellung eines Punktes B in Koord.Folge (b1,b2,...b(m)) bedeutdet nichts andesres als die Streckung/Stauchung und Drehung des Eins-Elementes, bis dieses zur Deckung mit Punkt B gebracht wurde, also eine Transformation des Eins-Elementes.
In Matrix-Schreibweise:
(b1 b2 . . b(m)) *(e1 e2 . . e(m))T
oder:
(a11 a12 . . . a1(m)) *(e1) =(b1)
(a21 a22 . . . a2(m)) *(e2) =(b2)
. . . . . .
(a(n,1) a(n,2) . . a(n,m)) *(e(m)) =(b(m)) ,
wenn der Umweg über n-Punkte {p(i)} :
p(i) =(ai,1 , .... ,ai,1) ,i=1...n genommen wurde, wie oben im Beispiel der Grafik mit P1 und P2.
Folgerung: Wenn statt Eins-Vektor (1,1,..) einen beliebigen anderen Vektor, z.B.: (x1,x2,..), einsetzt, erhält man die allg. Form eines Lin.GL.Systems mit n-Zeilen und m-Spalten. In Matrix(M)-Schreibweise:
(a(1,1) a(1,2) . . a(1,m)) *(x1 x2 . . x(m))T
(a(2,1) a(2,2) . . a(2,m))
. . . . . .
(a(n,1) a(n,2) . . a(n,m))
oder:
M*(x1 x2 . . x(m))T =(b1 b2 . . b(m))T
Dies bedeutet geometrisch: Es soll ein noch unbekannter Vektor=Pkt.X im Raum ermittelt werden, der durch Streckung/Stauchung und Drehung, was gleich-bedeutend ist mit n-Lin.Komb.(=Umwege über n andere Pkte.), zur Deckung mit einem anderen vorgegebenen Pkt.B gebracht werden kann. Achtung: Zum Zeitpunkt der Kreation einer solchen Fragestellung, ist noch nicht klar, ob dies auch wirklich funktioniert.
Am einfachsten ist diese Fragestellung noch zu lösen, wenn man von echten m-linear unabhängigen Richt.(=Punkten p(i)) im Rm ausgeht, die also in "alle Ecken des Raumes zeigen", und anschließend die L((p1...pm)*X) =B bildet. Das funktioniert dann auf jeden Fall unter dieser Voraussetzung.
Also gilt auch umgekehrt: B=(b1,...,b(m)) =L(P1,...,P(n)):

(P1+P2)+(B-(P1+P2) oder P2+(B-P2) etc.
Koord.Vergleich:
P1=(a11,a12), P2=(a21,a22), z.B.:
(P1+P2)+(B-(P1+P2) =
=> 1.Koord.: a11+a11 +b1-(a11+a21) =b1
2.Koord.: a12+a12 +b1-(a12+a22) =b2
= (b1,b2) =B
Schlussfolgerung: Um zu seinem Ziel zu gelangen, kann man viele Umwege gehen, oder direkt sein Ziel auf kürzestem Weg ansteuern!
Die Lösung ist, die Normierung aller Wege (=Lin.Komb.), die zu B führen, in dem man als Ausgangspunkt das Eins-Element des Raumes, hier (e1,e2)=(1,1), wählt:
b1*e1 +b2*e2 +....+b(m)*e(m) =B(b1,b2,..)
Def.: Die Darstellung eines Punktes B in Koord.Folge (b1,b2,...b(m)) bedeutdet nichts andesres als die Streckung/Stauchung und Drehung des Eins-Elementes, bis dieses zur Deckung mit Punkt B gebracht wurde, also eine Transformation des Eins-Elementes.
In Matrix-Schreibweise:
(b1 b2 . . b(m)) *(e1 e2 . . e(m))T
oder:
(a11 a12 . . . a1(m)) *(e1) =(b1)
(a21 a22 . . . a2(m)) *(e2) =(b2)
. . . . . .
(a(n,1) a(n,2) . . a(n,m)) *(e(m)) =(b(m)) ,
wenn der Umweg über n-Punkte {p(i)} :
p(i) =(ai,1 , .... ,ai,1) ,i=1...n genommen wurde, wie oben im Beispiel der Grafik mit P1 und P2.
Folgerung: Wenn statt Eins-Vektor (1,1,..) einen beliebigen anderen Vektor, z.B.: (x1,x2,..), einsetzt, erhält man die allg. Form eines Lin.GL.Systems mit n-Zeilen und m-Spalten. In Matrix(M)-Schreibweise:
(a(1,1) a(1,2) . . a(1,m)) *(x1 x2 . . x(m))T
(a(2,1) a(2,2) . . a(2,m))
. . . . . .
(a(n,1) a(n,2) . . a(n,m))
oder:
M*(x1 x2 . . x(m))T =(b1 b2 . . b(m))T
Dies bedeutet geometrisch: Es soll ein noch unbekannter Vektor=Pkt.X im Raum ermittelt werden, der durch Streckung/Stauchung und Drehung, was gleich-bedeutend ist mit n-Lin.Komb.(=Umwege über n andere Pkte.), zur Deckung mit einem anderen vorgegebenen Pkt.B gebracht werden kann. Achtung: Zum Zeitpunkt der Kreation einer solchen Fragestellung, ist noch nicht klar, ob dies auch wirklich funktioniert.
Am einfachsten ist diese Fragestellung noch zu lösen, wenn man von echten m-linear unabhängigen Richt.(=Punkten p(i)) im Rm ausgeht, die also in "alle Ecken des Raumes zeigen", und anschließend die L((p1...pm)*X) =B bildet. Das funktioniert dann auf jeden Fall unter dieser Voraussetzung.
4.8 Geometr.Deutung des Gauß-Elim.-Algo.
Der Gauß'schen-Eliminierungs-Algorithmus(GEA) bringt eine n,m Matrix auf Diagonal-
Form, wobei nach max. n-Zeilen (m>n) Schluß ist und der Rest eine (m-n)-fache Lösungs-
Mannigfaltigkeit darstellt. Wir können deshalb ohne Einschränkung der Allgemeinheit
bei den nachf. Betrachtungen von einer m,m Matrix ausgehen.
Um die Logik des GEA zu verstehen, betrachte man die nachf. Grafik:
Bild , Anal-geo10.jpg
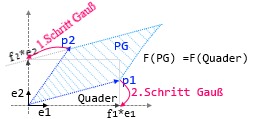
Schritt (j) GEA: Das Vielfache einer Zeile(Vektor) wird zu einer anderen Zeile(Vektor) hinzu addiert.
Ergebnis:
Nach max. m² Schritten hat man die Matrix auf eine Hauptachsen-Diagonal-Matrix gebracht, und die f(i)-Werte bilden die Haupt-Achse.
Entspr. Grafik sind die f(i) reelle Faktoren auf den zugehörigen Haupt-Achsen, dergestallt, daß das von den Vektor-Koord. F=(f1,...,f(m)) aufgespannte Quader-Volumen dem Volumen des m-dim Spates gleich ist, welches von den Zeilen-Vektoren {p(i)} aufgespannt wird.
Oder anders gesagt: die f(i) sind Kanten-Längen eines m-dim Quaders, dessen Seiten(Kanten) mit den entspr. e(i)-Richtungen parallel sind und wobei das Quader- Volumen Vol(f1...f(m)) =Vol(p1...p(m)) ist.
Folgerung: sind die {p(i)} lin. unabhängig, so können die Lösungs-Werte x(i) mittels Division b'(i)/f(i) ermittelt werden (Cramer'sche Regel). Dabei sind die b'(i) die bei jedem Schritt mit transformierten b(i) ->b'(i).
Der Lösungsvektor X ist eindeutig.
Beispiel:
Matrix: Ze=2, Sp=2
----x1----x2----b(i)----
(1) 5 3 = 2
(2) -2 1 = -4
Dreiecks-Matrix (nach GEA)
----x1----x2-----b'(i)-----
(1) 5 0 = 6,3636
(2) 0 2,2 = -3,2
Ergebnis (Lösung):
x1= 1,27
x2= -1,45
Vertauschen der Zeilen:
(2) -2 1 = -4
(1) 5 3 = 2
Dreiecks-Matrix (nach GEA)
(2) -2 0 = -2,54
(1) 0 5,5 = 8
Ergebnis (Lösung):
x1= 1,27
x2= -1,45
=> der Vektor (1.27, -1.45) wird zu (2,-4) transformiert, mittels Matrix(M) =
( 5 3)
(-2 1) ,siehe nachf. Grafik
Bild , Anal-geo11.jpg
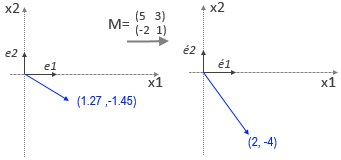
Das Vol()=Det(M) ist immer 11, nur das Vz wechselt, wenn die {p(i)} untereinander vertauscht werden. (Wir werden später untersuchen, welche geometr. Bedeutung das Vol() der Abb. hat)
Um die Logik des GEA zu verstehen, betrachte man die nachf. Grafik:

Schritt (j) GEA: Das Vielfache einer Zeile(Vektor) wird zu einer anderen Zeile(Vektor) hinzu addiert.
Ergebnis:
Nach max. m² Schritten hat man die Matrix auf eine Hauptachsen-Diagonal-Matrix gebracht, und die f(i)-Werte bilden die Haupt-Achse.
Entspr. Grafik sind die f(i) reelle Faktoren auf den zugehörigen Haupt-Achsen, dergestallt, daß das von den Vektor-Koord. F=(f1,...,f(m)) aufgespannte Quader-Volumen dem Volumen des m-dim Spates gleich ist, welches von den Zeilen-Vektoren {p(i)} aufgespannt wird.
Oder anders gesagt: die f(i) sind Kanten-Längen eines m-dim Quaders, dessen Seiten(Kanten) mit den entspr. e(i)-Richtungen parallel sind und wobei das Quader- Volumen Vol(f1...f(m)) =Vol(p1...p(m)) ist.
Folgerung: sind die {p(i)} lin. unabhängig, so können die Lösungs-Werte x(i) mittels Division b'(i)/f(i) ermittelt werden (Cramer'sche Regel). Dabei sind die b'(i) die bei jedem Schritt mit transformierten b(i) ->b'(i).
Der Lösungsvektor X ist eindeutig.
Beispiel:
Matrix: Ze=2, Sp=2
----x1----x2----b(i)----
(1) 5 3 = 2
(2) -2 1 = -4
Dreiecks-Matrix (nach GEA)
----x1----x2-----b'(i)-----
(1) 5 0 = 6,3636
(2) 0 2,2 = -3,2
Ergebnis (Lösung):
x1= 1,27
x2= -1,45
Vertauschen der Zeilen:
(2) -2 1 = -4
(1) 5 3 = 2
Dreiecks-Matrix (nach GEA)
(2) -2 0 = -2,54
(1) 0 5,5 = 8
Ergebnis (Lösung):
x1= 1,27
x2= -1,45
=> der Vektor (1.27, -1.45) wird zu (2,-4) transformiert, mittels Matrix(M) =
( 5 3)
(-2 1) ,siehe nachf. Grafik

Das Vol()=Det(M) ist immer 11, nur das Vz wechselt, wenn die {p(i)} untereinander vertauscht werden. (Wir werden später untersuchen, welche geometr. Bedeutung das Vol() der Abb. hat)
Bemerkung:
Da diese Transformation durch M mit jedem Pkt. des Raumes passiert, wenn B flexibel ist, wird der gesamte Raum, hier R², gedehnt/gestaucht und gedreht. Siehe dazu nachf. Abschnitt 4.9
Da diese Transformation durch M mit jedem Pkt. des Raumes passiert, wenn B flexibel ist, wird der gesamte Raum, hier R², gedehnt/gestaucht und gedreht. Siehe dazu nachf. Abschnitt 4.9
4.9 Die Lineare Abbildung im Rm:
Die lin.Abb. hat üblicher Weise die Form eines LGL-Systems. Symb.:
(M)XT=BT .
Def.1: Matrix(M) ist eine Folge von r*k reellen Zahlen, die in Rechteckform in r-Spalten und k-Zeilen angeordnet sind.
X,B sind Folgen von reellen Zahlen, also Elemente/Punkte des Eukl.Raumes. Die Anordnung in Koord.Schreibweise waagerecht oder senkrecht( T ) wird alternativ auch als Vektor (= Zeilen- oder Spaltenvektor) bezeichnet.
Folgerung: Wenn es um Abb. im Rm geht, sind X und B m-anzahlige Folgen.
Die Verknüpfung einer Matrix mit Punkten des Raumes ist zunächst eine links-seitige-skalare-Multiplikation, also Skapro(Mi,X), M(i)= i-ter Zeilen-Vektor mit X-Spaltenvektor.
Da das Skapro() gleichlange Vektoren erfordert, muß M die Spalten-Zahl m haben.
Ist bei einer (n,m) Matrix n>m, so ist das auch nicht sinnvoll, weil beim Durchmultiplizieren (Skapro's(Mi,X) =bi), ein längerer B-Vektor erforderlich wäre, was aber durch B∈Rm ausgeschlossen ist.
Also kommen für lin.Abb. im Rm nur (n,m)-Matrizen, n≤m in Frage. Bei n-Zeilen, n<m, gibt es allerdings für B nur n-signifikante=feste Werte in der Folge von m möglichen, was bedeutet, daß die fehlenden nicht festgelegt sind, und deshalb den Spielraum für die Lösungs-Mannigfaltigkeit geben.
Beispiel: B=(b1,b2,b3,...) , hier sind nur 3 von m-Dim. vorgegeben, also hat der Lös.-Raum (m-3)-Dim.
Def.2: Die lin.Abb. wird durch eine Matrix, wie zuvor beschrieben, repräsentiert.
Eigenschaften von M =lin.Abb.:
Vol(M)=Det(M) gleich Null oder ungleich Null.
1. Ist Vol(M)≠0, (=m-dim Spat, welches von den (n=m)-Zeilen- Vektoren von M aufgespannt wird), so handelt es sich um eine vollst. Abbildung des Eukl. Raumes in sich: Rm->Rm ,d.h., jeder Pkt. wird, (als Richtung betrachtet), gestreckt/gestaucht und gedreht.
Beispiel1: R2 als Gauß'sche Zahlen-Ebene, wo die z,w-Punkte durch, z.B. eine konforme Abb.f, ebenfalls gedehnt/gedreht werden: w=f(z).
M kommt besonders in 2 Formen zur Anwendung:
Koord.Transform. und Lin.Komb.
Beispiel2: (M){e(i)} ={é(i)}, hier wird Koord.Basis {e1,,e2,...} in eine andere, i.a. schiefwinklige, Koord.Basis {é1, é2,...} transformiert.
Beispiel3: Jeder Pkt.A des Raumes ist Lin.Komb der Basis-Vektoren {e(i)} = a(1)e1 +a(2)e2 +... oder lin.Abb. M=Eins()*AT:
(1 0 0 ... 0)
(0 1 0 ... 0)
(0 0 1 ... 0)
. .. . . . . .
(0 0 0 ... 1) =Eins()*AT=A
Die Lin.komb./lin.Abb ist also eine Abb. des Raumes in sich, oder Operator() im Rm, wie im Abschnitt 4.4 "Lineare Gleich. Systeme" bereits angesprochen wurde.
Achtung: Da offenbar M Linien in Linien abbildet, heißt sie deshalb auch:
Lineare Abbildung
Weitere Eigenschaft: Durch schrittweise Anwendung des Gauß-Algo ändert sich am Ergebnis der M-Abb. nichts:
(M->M'->M'')XT=B ,M'= Vielfaches einer Zeile zu einer Anderen add, solange sich Vol()=Det() nicht ändert.
Folgerung: Man kann zu den verschiedenen Matrizen, die zu einer lin.Abb. gehören, die Dreiecks-Matrix als Norm-Endzustand oder als Repäsentant einer lin.Abb. betrachten.
Die Menge aller lin.Abb. (auf der Menge der m-Tupel reeller Zahlen) ist dann unter diesem Aspekt betrachtet, selbst ein eigenständiger ,linearer-metrischer Raum.
Ist M=Einheits-Matrix =Eins(), so folgt aus Eins()*XT=XT, daß die Eins() als Eins-Element im Eukl.Raum fungiert.
2. Vol(M)=0: Dem m-dim Spat fehlen 1 oder mehere Dim., d.h., das m-dim Volumen ist betragsmäßig Null!
Das wiederum bedeutet: >1 Anz. Zeilen-Vektoren in M sind lin.abhängig und können aus M entfernt werden, tragen also zur lin.Abb. nichts bei.
Dies wiederum bedeutet, mann kann n=m-k setzen, k=Anz. unsinniger Zeilen.
Ist Vol(M)=0 , so folgt M =Matrix(n,m) , n <m.
Folgerung: M bildet nicht mehr den gesamten Raum ab, sondern nur noch einen Unterraum in einen anderen Unterraum.
Im LGL-System macht sich das durch einen Lösungsraum, (m-n)-dim Hyperebene im Rm, bemerkbar, siehe Beispiel hinter Abschnitt 4.5.
Jetzt kann man geometr. zu M einen Graph angeben:
Graph(M): { (x1,..,x(m)}: (M)XT=BT }
Man hat hier offenbar in der Menge von m-Variablen, nur n unabhängige Variable und (m-n) von den anderen abhängige Variable.
Umgekehrt gilt: ist n=m, hat man keinen Graph. (Lös.-Menge hat Ausdehnung Null)
Beispiel: { (x,y): x-3y +4=0 }:
Interpretation: m=2, n=1, die (hier entartete) Det() ist 1/3, Die (2-1)-dim Hyperebene im R2 ist eine Greade, so daß der Graph sich hier als eine Gerade in der Ebene durch die Pkt.(0,4/3) und (-4,0) darstellt und den Anstieg 1y/3x hat.
Es können hier x,y(x) und x(y),y abhäng./unabhäng. Variable sein.
Def.1: Matrix(M) ist eine Folge von r*k reellen Zahlen, die in Rechteckform in r-Spalten und k-Zeilen angeordnet sind.
X,B sind Folgen von reellen Zahlen, also Elemente/Punkte des Eukl.Raumes. Die Anordnung in Koord.Schreibweise waagerecht oder senkrecht( T ) wird alternativ auch als Vektor (= Zeilen- oder Spaltenvektor) bezeichnet.
Folgerung: Wenn es um Abb. im Rm geht, sind X und B m-anzahlige Folgen.
Die Verknüpfung einer Matrix mit Punkten des Raumes ist zunächst eine links-seitige-skalare-Multiplikation, also Skapro(Mi,X), M(i)= i-ter Zeilen-Vektor mit X-Spaltenvektor.
Da das Skapro() gleichlange Vektoren erfordert, muß M die Spalten-Zahl m haben.
Ist bei einer (n,m) Matrix n>m, so ist das auch nicht sinnvoll, weil beim Durchmultiplizieren (Skapro's(Mi,X) =bi), ein längerer B-Vektor erforderlich wäre, was aber durch B∈Rm ausgeschlossen ist.
Also kommen für lin.Abb. im Rm nur (n,m)-Matrizen, n≤m in Frage. Bei n-Zeilen, n<m, gibt es allerdings für B nur n-signifikante=feste Werte in der Folge von m möglichen, was bedeutet, daß die fehlenden nicht festgelegt sind, und deshalb den Spielraum für die Lösungs-Mannigfaltigkeit geben.
Beispiel: B=(b1,b2,b3,...) , hier sind nur 3 von m-Dim. vorgegeben, also hat der Lös.-Raum (m-3)-Dim.
Def.2: Die lin.Abb. wird durch eine Matrix, wie zuvor beschrieben, repräsentiert.
Eigenschaften von M =lin.Abb.:
Vol(M)=Det(M) gleich Null oder ungleich Null.
1. Ist Vol(M)≠0, (=m-dim Spat, welches von den (n=m)-Zeilen- Vektoren von M aufgespannt wird), so handelt es sich um eine vollst. Abbildung des Eukl. Raumes in sich: Rm->Rm ,d.h., jeder Pkt. wird, (als Richtung betrachtet), gestreckt/gestaucht und gedreht.
Beispiel1: R2 als Gauß'sche Zahlen-Ebene, wo die z,w-Punkte durch, z.B. eine konforme Abb.f, ebenfalls gedehnt/gedreht werden: w=f(z).
M kommt besonders in 2 Formen zur Anwendung:
Koord.Transform. und Lin.Komb.
Beispiel2: (M){e(i)} ={é(i)}, hier wird Koord.Basis {e1,,e2,...} in eine andere, i.a. schiefwinklige, Koord.Basis {é1, é2,...} transformiert.
Beispiel3: Jeder Pkt.A des Raumes ist Lin.Komb der Basis-Vektoren {e(i)} = a(1)e1 +a(2)e2 +... oder lin.Abb. M=Eins()*AT:
(1 0 0 ... 0)
(0 1 0 ... 0)
(0 0 1 ... 0)
. .. . . . . .
(0 0 0 ... 1) =Eins()*AT=A
Die Lin.komb./lin.Abb ist also eine Abb. des Raumes in sich, oder Operator() im Rm, wie im Abschnitt 4.4 "Lineare Gleich. Systeme" bereits angesprochen wurde.
Achtung: Da offenbar M Linien in Linien abbildet, heißt sie deshalb auch:
Weitere Eigenschaft: Durch schrittweise Anwendung des Gauß-Algo ändert sich am Ergebnis der M-Abb. nichts:
(M->M'->M'')XT=B ,M'= Vielfaches einer Zeile zu einer Anderen add, solange sich Vol()=Det() nicht ändert.
Folgerung: Man kann zu den verschiedenen Matrizen, die zu einer lin.Abb. gehören, die Dreiecks-Matrix als Norm-Endzustand oder als Repäsentant einer lin.Abb. betrachten.
Die Menge aller lin.Abb. (auf der Menge der m-Tupel reeller Zahlen) ist dann unter diesem Aspekt betrachtet, selbst ein eigenständiger ,linearer-metrischer Raum.
Ist M=Einheits-Matrix =Eins(), so folgt aus Eins()*XT=XT, daß die Eins() als Eins-Element im Eukl.Raum fungiert.
2. Vol(M)=0: Dem m-dim Spat fehlen 1 oder mehere Dim., d.h., das m-dim Volumen ist betragsmäßig Null!
Das wiederum bedeutet: >1 Anz. Zeilen-Vektoren in M sind lin.abhängig und können aus M entfernt werden, tragen also zur lin.Abb. nichts bei.
Dies wiederum bedeutet, mann kann n=m-k setzen, k=Anz. unsinniger Zeilen.
Ist Vol(M)=0 , so folgt M =Matrix(n,m) , n <m.
Folgerung: M bildet nicht mehr den gesamten Raum ab, sondern nur noch einen Unterraum in einen anderen Unterraum.
Im LGL-System macht sich das durch einen Lösungsraum, (m-n)-dim Hyperebene im Rm, bemerkbar, siehe Beispiel hinter Abschnitt 4.5.
Jetzt kann man geometr. zu M einen Graph angeben:
Graph(M): { (x1,..,x(m)}: (M)XT=BT }
Man hat hier offenbar in der Menge von m-Variablen, nur n unabhängige Variable und (m-n) von den anderen abhängige Variable.
Umgekehrt gilt: ist n=m, hat man keinen Graph. (Lös.-Menge hat Ausdehnung Null)
Beispiel: { (x,y): x-3y +4=0 }:
Interpretation: m=2, n=1, die (hier entartete) Det() ist 1/3, Die (2-1)-dim Hyperebene im R2 ist eine Greade, so daß der Graph sich hier als eine Gerade in der Ebene durch die Pkt.(0,4/3) und (-4,0) darstellt und den Anstieg 1y/3x hat.
Es können hier x,y(x) und x(y),y abhäng./unabhäng. Variable sein.
Bemerkung:
Wir werden später die allg. Graph-Definition einer Abbildung zusätzlich auch auf nicht-Lineare Abbildungen, (=Funktionen), ausdehnen.
Wir werden später die allg. Graph-Definition einer Abbildung zusätzlich auch auf nicht-Lineare Abbildungen, (=Funktionen), ausdehnen.
4.10 Auflösungs-Theorie:
m=m Matrizen:
Zuerst betrachten wir die Abb. aus Beispiel: im Abschnitt 4.8 zuvor unter der Fragestellung: Wie werden Teilmengen, delta-Umgebungen, oder allg. geometr. Objekte durch lin.Abb., also (m,m)-Matrizen(M), transformiert.
Im nachf.Bild werden 3Punkte A,B,C durch M() in A',B',C' abgebildet, also, wie üblich gedehnt u.gedreht.
Das Dreieck(ABC) geht dabei in Dreieck(A,B,C) über:
Bild , Anal-geo12.jpg
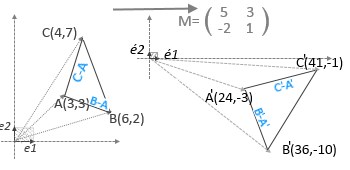
Die Fläche im 1.Dreieck ist entspr. Flächen-Prokukt (B-A)x(C-A):
(3,-1)x(1,4) = 3*4 -(-1*1) =13[e1e1]
Im rechten Dreieck (B'-A')x(C'-A'):
(12,-7)x(17,2) = 12*2 -(-7*17) =143[e1'e1']
Setzt man beide Flächen ins Verhältnis, so erhält man:
143/13 = 11 ,Das ist das Vol(M)=Det(M) der zugehörigen lin.Abb.
Satz: Bei einer Abb. drückt die Determinante der Abb., wenn sie ungleich Null ist, das Volumenverhältnis zwischen Quell und Zielmenge aus, insbesondere zwischen den Eins-Elementen im Quell-Raum und Ziel-Raum. (Diese Aussage bezieht sich erst-einmal nur auf lin.Abb, da es hier keine Rolle spielt, wo im Raum sich die Objekte befinden)
n<m Matrizen:
1. Die einfachste Abb. im R² ist : (M)XT=c , mit X=(x1,x2) und M=(a b), d.h., M besteht nur aus 1-Zeilen-Vektor(a,b) und B=(b1,b2)=c ist reele Zahl. Die zugehörige LGL lautet:
(GL1): a*x1 +b*x2 =c
Die Gl1 besagt, x1,x2 sind voneinander abhängig, und man kann nach x1 auflösen, wenn a≠0 und nach x2, wenn b≠0 ist.
x1 frei: Lös.Menge ist x2(x1)= -b/a *x2 +c
x2 frei: Lös.Menge ist x1(x2)= -a/b *x1 +c
(Da lin.Abb. den gesamten Raum abbilden, kann GL1 an jedem Ort im R² nach der einen oder anderen Variablen aufgelöst werden).
Der Graph von (M)XT=c für Auflösung nach z.B. x2 wäre dann:
{(x1,x2(x1)): x2()=(-a/b *x1 +c) }
Zur besseren Optik werden die abhäng.Var. mit yj bezeichnet:
=>{(x,y)): y=f(x)=(-a/b *x +c) }
2. M=(a1,a2,..), X=(x1,x2,...) ,B=(b1,b2,...)=c
M= 1-ZeilenVektor, => 1-lineare Bedingung und es kann nach jedem x(i) aufgelöst werden, wenn a(i)≠0 ist:
{(x1, y ,x3,..)): y=f(-a1/a2*x1
-a3/a2*x3 ) + ...}
Der Graph ist eine Linie im Raum.
n<m Matrizen ,n>1:
Hier hat M mehr als einen Zeilen-Vektor, also echte Matrix, und die Auflösung nach einer bestimmten x-Indexfolge {x(i)}, i=Teilindexfolge der len(m-n) aus {1...m}, ist möglich wenn die entspr. Koeff.Det()≠0 ist.
Die Vorgehensweise wird an einem Beispiel einer (3,5)-Matrix demonstriert:
Beispiel1:
Matrix(M): n=Ze=3, m=Sp=5
----x1---x2--x3---x4---x5----b(i)
(1) 5 3 1 4 2 = 2
(2) 1 2 4 1 2 = 3
(3) 2 6 12 3 1 = 0
Dreieck nach GEA:
----x1---x2----x3----x4-----x5------b(i)
(1) 5 0 0 0 25 = 45
(2) 0 1,4 0 2,1 -12,4 = -23,24
(3) 0 0 -1,4 ,71 -5,28 = -9,714
Ergebnis:
Nach x1,x2,x3 auflösbar, wegen Det()≠0 der 1-3 Spalten. Unabhäng. Variable sind x4,x5 .
Beispiel2: Jetzt wird Sp.1 ans Ende verschoben:
(x2) (x3) (x4) (x5) (x1) (Beisp.1)
----x1---x2--x3---x4---x5----b(i)
(1) 3 1 4 2 5 = 2
(2) 2 4 1 2 1 = 3
(3) 6 12 3 1 2 = 0
Dreieck nach GEA:
(1) 3 0 0 ∞ ∞ = ∞
(2) 0 3,3.. 0 -∞ -∞ = -∞
(3) 0 0 0.0 -5 -1 = -9
Ergebnis:
Nach x2,x3,x4, in Abhängigkeit der Var.x4,x5, nicht auflösbar, wegen Det()=0 der 1-3 Spalten. (Die durch lin.Abb.M transform. Unterräume, Quelle u.Ziel, müssen gleiche Dim. haben!)
Aber: Beisp.2 läßt sich dennoch auflösen, wenn Sp.(5,1,2) verwendet werden, (3,4) unabhäng.Var.:
x1=L1(x3,x4), x2=L2(x3,x4), x5=L3(x3,x4)
x1=x(2)= -16,60 -1,50y1 +8,90y2
x2=x(3)= 6,80 +0,50y1 -3,70y2
x3=x(4)= 0 +y1
x4=x(5)= 0 +y2
x5=x(1)= 9,00 0y1 -5,00y2
(y(i)=reell, frei wählbar
Fazit: Es sind i.a. nicht alle Lös.Raum-Kombinationen möglich. Es müssen alle Kombinationen, hier n=3 von 5, geprüft werden. Die mögl. Lösungen sind auch tatsächlich alle unterschiedlich!
Nachf. ein Algorithmus für Auflösung von (n,m)-Matrizen, m>n:
Zuerst betrachten wir die Abb. aus Beispiel: im Abschnitt 4.8 zuvor unter der Fragestellung: Wie werden Teilmengen, delta-Umgebungen, oder allg. geometr. Objekte durch lin.Abb., also (m,m)-Matrizen(M), transformiert.
Im nachf.Bild werden 3Punkte A,B,C durch M() in A',B',C' abgebildet, also, wie üblich gedehnt u.gedreht.
Das Dreieck(ABC) geht dabei in Dreieck(A,B,C) über:

Die Fläche im 1.Dreieck ist entspr. Flächen-Prokukt (B-A)x(C-A):
Im rechten Dreieck (B'-A')x(C'-A'):
Setzt man beide Flächen ins Verhältnis, so erhält man:
143/13 = 11 ,Das ist das Vol(M)=Det(M) der zugehörigen lin.Abb.
Satz: Bei einer Abb. drückt die Determinante der Abb., wenn sie ungleich Null ist, das Volumenverhältnis zwischen Quell und Zielmenge aus, insbesondere zwischen den Eins-Elementen im Quell-Raum und Ziel-Raum. (Diese Aussage bezieht sich erst-einmal nur auf lin.Abb, da es hier keine Rolle spielt, wo im Raum sich die Objekte befinden)
Kosmologische Überlegungen:
Die lin. Abb. dehnt und dreht den Raum an jeder Stelle, egal wo, mit einen festen Faktor für Ausdehnung und Drehung. dabei gilt, Det()>1 bedeuteut Ausdehnung /Expansion und Det()<1 Schrumpfung. Auf das Universum übertragen heißt das, laut lez.Beobachtungen, das Universum dehnt sich aus, expandiert, aber nicht linear, da die Beobachtungen zeigen, daß je weiter man ,(von Null), weg ist, desto schneller expandiert es. Die zugehörige Determinante ist dann eine Funktion des Ortes Det(X), X=Ortsvektor im Raum. Die Zeilen-Vektoren in M sind keine Lin.Komb. mehr, sonder allg. stetige Funktionen F(X) =(f1(X) ,f2(X), f3(x)), wenn der Raum 3-dim ist. Die Determinante berechnet sich dann über:
δ(f1,f2,f3) /δ(x1,x2,x3) ,für jeden Ort berechnet.
F: dF= g(r)*dr , g nicht lin.Funktion, wachsend mit r=Abstand.
Die lin. Abb. dehnt und dreht den Raum an jeder Stelle, egal wo, mit einen festen Faktor für Ausdehnung und Drehung. dabei gilt, Det()>1 bedeuteut Ausdehnung /Expansion und Det()<1 Schrumpfung. Auf das Universum übertragen heißt das, laut lez.Beobachtungen, das Universum dehnt sich aus, expandiert, aber nicht linear, da die Beobachtungen zeigen, daß je weiter man ,(von Null), weg ist, desto schneller expandiert es. Die zugehörige Determinante ist dann eine Funktion des Ortes Det(X), X=Ortsvektor im Raum. Die Zeilen-Vektoren in M sind keine Lin.Komb. mehr, sonder allg. stetige Funktionen F(X) =(f1(X) ,f2(X), f3(x)), wenn der Raum 3-dim ist. Die Determinante berechnet sich dann über:
δ(f1,f2,f3) /δ(x1,x2,x3) ,für jeden Ort berechnet.
F: dF= g(r)*dr , g nicht lin.Funktion, wachsend mit r=Abstand.
n<m Matrizen:
1. Die einfachste Abb. im R² ist : (M)XT=c , mit X=(x1,x2) und M=(a b), d.h., M besteht nur aus 1-Zeilen-Vektor(a,b) und B=(b1,b2)=c ist reele Zahl. Die zugehörige LGL lautet:
(GL1): a*x1 +b*x2 =c
Die Gl1 besagt, x1,x2 sind voneinander abhängig, und man kann nach x1 auflösen, wenn a≠0 und nach x2, wenn b≠0 ist.
x1 frei: Lös.Menge ist x2(x1)= -b/a *x2 +c
x2 frei: Lös.Menge ist x1(x2)= -a/b *x1 +c
(Da lin.Abb. den gesamten Raum abbilden, kann GL1 an jedem Ort im R² nach der einen oder anderen Variablen aufgelöst werden).
Der Graph von (M)XT=c für Auflösung nach z.B. x2 wäre dann:
=>
Diese Abb.Form erschließt die gesamte 1-dim Analysis, also Abb. von reellen
Zahlen in reelle Zahlen (R1 ->R1), wenn f nicht nur lineare,
sondern allg. stetige Funktion auf x ist.
2. M=(a1,a2,..), X=(x1,x2,...) ,B=(b1,b2,...)=c
M= 1-ZeilenVektor, => 1-lineare Bedingung und es kann nach jedem x(i) aufgelöst werden, wenn a(i)≠0 ist:
Der Graph ist eine Linie im Raum.
n<m Matrizen ,n>1:
Hier hat M mehr als einen Zeilen-Vektor, also echte Matrix, und die Auflösung nach einer bestimmten x-Indexfolge {x(i)}, i=Teilindexfolge der len(m-n) aus {1...m}, ist möglich wenn die entspr. Koeff.Det()≠0 ist.
Die Vorgehensweise wird an einem Beispiel einer (3,5)-Matrix demonstriert:
Beispiel1:
Matrix(M): n=Ze=3, m=Sp=5
----x1---x2--x3---x4---x5----b(i)
(1) 5 3 1 4 2 = 2
(2) 1 2 4 1 2 = 3
(3) 2 6 12 3 1 = 0
Dreieck nach GEA:
----x1---x2----x3----x4-----x5------b(i)
(1) 5 0 0 0 25 = 45
(2) 0 1,4 0 2,1 -12,4 = -23,24
(3) 0 0 -1,4 ,71 -5,28 = -9,714
Ergebnis:
Nach x1,x2,x3 auflösbar, wegen Det()≠0 der 1-3 Spalten. Unabhäng. Variable sind x4,x5 .
Beispiel2: Jetzt wird Sp.1 ans Ende verschoben:
(x2) (x3) (x4) (x5) (x1) (Beisp.1)
----x1---x2--x3---x4---x5----b(i)
(1) 3 1 4 2 5 = 2
(2) 2 4 1 2 1 = 3
(3) 6 12 3 1 2 = 0
Dreieck nach GEA:
(1) 3 0 0 ∞ ∞ = ∞
(2) 0 3,3.. 0 -∞ -∞ = -∞
(3) 0 0 0.0 -5 -1 = -9
Ergebnis:
Nach x2,x3,x4, in Abhängigkeit der Var.x4,x5, nicht auflösbar, wegen Det()=0 der 1-3 Spalten. (Die durch lin.Abb.M transform. Unterräume, Quelle u.Ziel, müssen gleiche Dim. haben!)
Aber: Beisp.2 läßt sich dennoch auflösen, wenn Sp.(5,1,2) verwendet werden, (3,4) unabhäng.Var.:
x1=L1(x3,x4), x2=L2(x3,x4), x5=L3(x3,x4)
x1=x(2)= -16,60 -1,50y1 +8,90y2
x2=x(3)= 6,80 +0,50y1 -3,70y2
x3=x(4)= 0 +y1
x4=x(5)= 0 +y2
x5=x(1)= 9,00 0y1 -5,00y2
(y(i)=reell, frei wählbar
Fazit: Es sind i.a. nicht alle Lös.Raum-Kombinationen möglich. Es müssen alle Kombinationen, hier n=3 von 5, geprüft werden. Die mögl. Lösungen sind auch tatsächlich alle unterschiedlich!
Nachf. ein Algorithmus für Auflösung von (n,m)-Matrizen, m>n:
Auflösung von (n,m)-Matrizen, m>n:
1.
Alle Zeilen-Vektoren aus M streichen, die ein Vielfaches einer
anderen Zeile sind. (n-1)!/2 Überprüfungen.
2.
Beliebige n-Indexfolge aus 1...m bilden. Dann die zugehörigen
Spalten zu der n-Indexfolge an den Anfang von M umordnen. GEA anwenden und
schauen, ob der Koeeff. á(n,n)≠0 ist. Wenn ja, hat man eine x-Indexfolge gefunden,
die man, wenn man mit der Indexfolge zufrieden ist, fertig lösen kann:
(Wie zuvor beschrieben durch part.Lös. inhom.System +Lös.Raum homog.System: x°+x' )
{x(i1),..., x(in)} abhängige Variable
{x(j1),..., x(jm-n)} unabhäng.Variable {y1,y2..}.
Die Indexfolgen:
{i1....in} und {j1....jm-n} ergänzen sich in {1....m}.
{x(j1),..., x(jm-n)} unabhäng.Variable {y1,y2..}.
Die Indexfolgen:
{i1....in} und {j1....jm-n} ergänzen sich in {1....m}.
3.
Wenn man nicht mit der unter 2. zufällig gefundenen Lösung
zufrieden ist, müssen alle Index-Kombinationen aus m!/n! durch gearbeitet werden.
(Im vorigen Beispiel: 120/6 =20 Kombi's):
Bei rechentechnischer Lösung muß dazu der GEA-UP-Algo. in einen übergeordneten 'Host'-Main() eingebunden werden, der die Punkte 1. und 2., diesen im Zykl., abarbeitet.
Bei rechentechnischer Lösung muß dazu der GEA-UP-Algo. in einen übergeordneten 'Host'-Main() eingebunden werden, der die Punkte 1. und 2., diesen im Zykl., abarbeitet.
Weitere Betrachtungen:
Euklidische Geometrie ,
Modell der reellen Zahlen ,
analytische Geometrie I ,
analytische Geometrie II ,
Euklidischer Raum ,
Analysis 1, Abbildungen ,
kleinere Beispiele der Himmelsmechanik im Newton-Modell ,
Bewegungen im Newton-Raum ,