6.0 Ausgangspunkt     ->6.1     ->Inhalts.Verz.
Im Kontext dieser Abhandlungen unterscheiden wir zwei Arten von Räumen:
1.   lokaler Raum unserer Anschauung.   Elemente sind: Objekte, Objekt-Eigenschaften, Wechselwirkungen, Ereignisse u.ä. im (beobachtbaren) 'Universum'.
Untersuchungs-Methoden sind: Mechanik (Newton'sche Axiomatik), Elektrodynamik, Relativitätsprinzip u.a. Weitere Bezeichnungen für den 'lokalen Raum' sind: 'phys.Raum' oder 'Newton Raum'
2.  Abstrakter (math.) Raum.   Elemente sind: Zahlen, m-Tupel von Zahlen und im weiteren Sinn: "Abstrakte math. Objekte", mit denen man "rechnen" kann.

Allen Räumen ist gemein, daß sie über eine Verknüpfungs-Axiomatik ihrer Elemente charakterisiert werden.
Damit eine Verbindung (Assoziierung) zwischen beiden Räumen hergestellt werden kann, wird ein abstrakter "Mengen-Begriff" eingeführt, (Menge von Elementen), und wie folgt verwendet:
Einer Menge M wird durch Indexierung ihrer Elemente E eine Folge-Eigenschaft zugeordnet: M={E(i)}, i=1,2,...     Die Indizes repräsentieren dann eine Abbildung in die Menge der "natürlichen Zahlen", dem einfachsten math. Raum. Über die verschiedenen Abstraktions-Stufen, siehe 'Dok.3_1: Modell der reellen Zahlen' , erhält man einen konkreten Zahl-Raum, nämlich, den Raum der "reellen Zahlen", symb.: R={r}, r=reell, mit dessen Elementen man nun alle bekannten Rechen-Operationen durchführen kann.

Wird die Menge der reellen Zahlen zu der Menge aller m-Tupel reeller Zahlen, {r₁,....,r_m}, r_i=reell erweitert, so bezeichnen wir diesen Menge als "(abstrakter) Euklid. Raum", symb.: R^m (R¹=Menge der reellen Zahlen).
Beispiel:   Die Ort-Eigenschaft von Körpern (Massen) im lokalen Raum kann den Punkten (Elementen) des R³ zugeordnet werden, und die zugehörige Temperatur-Eigenschaft einer reellen Zahl im R¹.

Verknüpfungs-Axiomatik für die Elemente des R^m:
- Add/Sub:   p1±p2=((x₁±y₁),...,(x_m±y_m))
- Mult/Div:   nicht definiert! (außer R¹)
- Mult. mit reeller Zahl:   λp1=(λx₁,...,λx_m)
- Lin.-Komb.:   L(p1,..,pn)= a₁p₁ +...+a_np_n
Definition spez. Verknüpf.:
- Len:     Len(p1-p2)= -Len(p2-p1) ,±Länge einer Richtung
- Skapro:   <p1,p2> = x₁*y₁+...+ x_m*y_m
- Norm:     Norm(p1)= (+)Sqrt(Skapro(p1,p1))
- Metrik:    d(p1,p2)= Norm(p1-p2)=  (+)Sqrt((x₁-y₁)²+...+(x_m-y_m)²)
Diese 'Metrik' wird auch als "Euklid.Abstand" bezeichnet.
- Volumenprodukt:   Vol(p1...pm)= Det(p1...pm)
- Flächenprodukt:   F(p1*p2)= -F(p2*p1)
F() ist die orientierte Fläche des von p1,p2 aufgespannten Parallelogramm im R^m.
Beachte:  Da die Elemente des R^m (auch) Richtungen sind, werden die Verknüpfungen bei Richtungswechsel, also p1=-(-p1), mit (-1) multipliziert. Dies gilt auch bei Vertauschung 2-er Elemente (ausser Add, Skapro, Norm, Metrik ).

Koordinaten-Systeme:
Koord.Basis ist E={e₁,...e_m} , e_j=(0,..,1,..,0); (1 an der j-ten Stelle)
E ist eine Menge von m Richtungen der Länge=1, die auf den zugehörigen Koord.Achsen liegen, also:
e_j= (Null-->e_j)= (e_j-Null) ; e_j= x_j/Len(x_j,0) (bei x_j≠Null).
In der geometrischen Assoziierung werden die {e_j} als paarweise rechtwinklig gedeutet, also:
i≠j : Skapro(e_i, e_j)=0 ,F(e_i, e_j)=±1
i=j : Skapro(e_i, e_i)=1 ,F(e_i, e_i)=0
Dieses Basis-System E wird auch als 'karth.-Koord.-System' bezeichnet.
Alle Verknüpfungen können sowohl in der Koeffizienten-Schreibweise (ohne e_i) geschrieben werden (skalare Schreibweise), als auch in der Lin.-Komb.-Schreibweise (mit e_i), sogenannte "Richtungs-/Vektor-Schreibweise" .


Beginnen wollen wir mit der Mittel-/Schwerpunkt-Berechnung.

Begriffsbildung und Sachverhalt:  
Bei den Begriffen: Mittel- /Gleichgewichts- /Schwer- Punkt etc. handelt es sich im Allgemeinen immer um den gleichen Sachverhalt, nämlich:
Berechnung des gewichteten Mittels einer Element-Folge:
M={f_j*p_j} , f_j=reelle Zahlen.
Dieses gew.Mittel, (sogenannt, weil in der Folge M{} Ort-Koordinaten p mit einem "Gewicht/Faktor"=f multipliziert werden), wird dann im gegebenen Quell-Kontext unterschiedlich gewertet, als zB.:
- Mittelpunkt oder Schwerpunkt
- arithmetisches Mittel (nur bei Folgen im R¹)
- Gleichgewicht bei stat.Momenten
- Geschlossene Richtungs-Polygon-Züge ( Sum(d_i)=0 )
Dieser Sachverhalt wird nachfolgend am Beispiel 2-er Elemente beschrieben.

Mittelpunkt zweier Elemente p1,p2:  
Sind nur die Ort-Koord. zu vermitteln, (alle f gleich oder =1), dann wird ein Punkt x auf der Geraden duch (p1,p2) gesucht, so dass die jeweiligen Abstände (Richtungs-Diff.) der Punkte zu x gleich sind.
Sind p1 und p2 zusätzlich noch mit einem Faktor gewichtet, so werden 2 Rechteck-Flächen gesucht, f(*p1-x) und g*(p2-x), die von der Fläche=F() her gleich sind,, also: f(p1-x)+g(p2-x)=0.
==>   Gl.1.1:   f*p1 +g*p2 -(f+g)*x=0
Bemerkung:   Da es sich bei Punkt-Differenzen, z.B. (p1-x), um Richtungen handelt, werden Produkte von reellen Zahlen * Richtung auch als 'stat.Moment' bezeichnet, welches betragsmäßig einer Rechteck-Fläche entspricht. Sind p1,p2 reelle Zahlen, z.B. Koord. der Punkte, so vereinfacht sich Gl.1.1 zu dem bekannten arithmetischen Mittel:
x =(f*p1 +g*p1/(f+g) , f,g,p1,p2 reell
Sind die Punkte gleichgewichtet : f=g oder neutral-gewichtet: f=g=1, dann gilt: x=(p1+p2)/2

Gewichtetes Mittel p1,p2:   Bild-Auswertung:
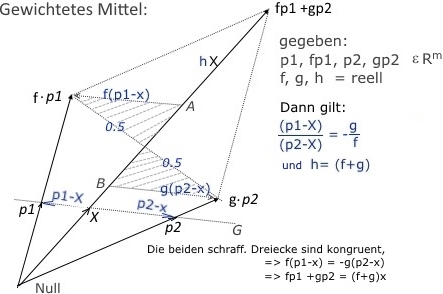
Alle Punkte p1,p2,fp1,gp2,Null liegen in einer Ebene.
Die 4 Dreiecke:   D1=(0,x,p1) ,D1a=(0,A,fp1)
und D2=(0,x,p1) ,D2a=(0,B,gp2)   sind paarweise aehnlich:
D1a =f*D1 und D2a =g*D2
Auch fuer die zu (p1-x) parallele Richtung (fp1-A) gilt dann (fp1-A) =f(p1-x).

Die Diagonalen des Parallelogramms schneiden sich in der Mitte. Dadurch sind die schraff.Dreiecke kongruent(1 Seite gleich und alle Winkel). Dadurch sind auch die beiden Richtungen f(p1-x) und g(p2-x) gleich (bis auf Vz.).
Also gilt: f(p1-x) +g(p2-x) =Null

x liegt allg. nicht in der Mitte von (p1-p2)
(p1-x)= [(f+g)*p1 -(f*p1+g*p2)]/(f+g)
          = g*(p1-p2) /(f+g)
(p2-x)= [(f+g)*p2 -(f*p1+g*p2)]/(f+g)
          = f*(p2-p1) /(f+g)
Aus (p1-x)/(x-p2) = g/f folgt:
Gl.1.2:   f*(p1-x) = g*(x-p2)   Der Mittelpunkt(Schwerpunkt) verschiebt sich in Richtung groesseres Gewicht, (hier f)!
Wichtig:   Neben den Gewichten f,g der Punkte p1,p2 hat natürlich auch der Pkt. x ein neues Gewicht, nämlich h=(f+g).   (f+g)*x ist dann als neuer, gewichteter Punkt zu verwenden, in Ersetzung des Punkte-Systems {f*p1, g*p2}.
Bemerkung:   Gl.1.2 drueckt eine Form der Hebel-Gesetze aus: "Last*Lastarm = Kraft*Kraftarm"

Mittelpunkt mehrerer Elemente p1,p2,...:  
Die Elemente mit den Orten {p1,p2,...} haben die Gewichte {f1,f2,...}
p' sei dann der Ort des gew.Mittel (Schwerpunkt) von f1*p1,f2*p2. p' hat dann das Gesamtgewicht der Pkte. p1,p2 als Gewichtung fuer weitere Berechnungen p'=(f1+f2)*p'.
Iterativ: Wird ein weiterer Pkt. z.B. f3*p3, mit (f1+f2)*p' gemittelt, so ergibgt sich als neuer gew.Mittelpunkt:
p''=((f1+f2)*p' +f3*p3) /(f1+f2+f3)   p' durch (f1*p1 + f2*p2) / (f1+f2) ersetzen
p''= (f1*p1 +f2*p2 +f3*p3*) /(f1+f2+f3)
Weitere Mittlungen mit p'' vornehmen usw.
Allg. fuer n-Elemente:  m= Sum(f_i*p_i)/Sum(f_i)

Die Koord. der allg. Schwerpunkt-Gleichung, siehe zuvor, lauten für die Punkte p_i=(a_i,1,...,a_i,m), i=1...n :
Sum(f_i)*m(m₁,..., m_m) =
        f1*(a_1,1, ... ,a_1,m)
     + f2*(a_2,1, ... ,a_2,m)
     + . . . . . . .
     + fn*(a_n,1, ... ,a_n,m)
Koord. sind Spalten j=1...m , m=( m₁,..., m_m):
m_j= (f₁a_1,j +f₂a_2,j + ... +f_na_n,j) /Sum(f_i)
Geometrische Interpretation der Schwerpunkt-Gleichung:
Sei X=(a_i,1,...,a_i,m) der Schwerpunkt, dann folgt:
Sum(f_i*p_i) -Sum(f_i)*X =0
=>   Sum(f_i*p_i) -Sum(f_i*X) =0   =>
Gl.1: Sum(f_i*(p_i - X))=0
Das unterstrichene Produkt in der Summierung wird nun als Flächeninhalt eines orientierten Rechteckes, mit Seiten f_i und p_i - X), interpretiert:
F_i= f_i*(p_i - X) ,   F_i= ± reelle Zahl   daraus folgt:
Satz 1:
Die Summe der Flächenmomente zwischen den (gewicht.) Punkten einer Punktfolge und ihrem Schwer- oder Mittelpunkt ist Null.

unendl.(stetige) Pkt.-Folgen:
{ (f₁,a),(f₂,b) } sei Punktfolge im R₁, also f_i, a, b reell.
Dann nehmen wir eine schrittweise Teilung des Intervall d=(b-a) sodass sich X in der n-ten Teilungsstufe wie folgt ergibt:
Sum(k: f_(k+1)*[a + k*d/n - X] ) =0   ,n>0 ;k=0,1,..n
In den Teilungsstufen ergeben sich folg. Pkt.Folgen:
n=1:   {f₁a +0, f₂a+1*d/1 }   = {f₁a , f₂b}
n=2:   {f₁a+0, f₂a+1*d/2 , f₃a+2*d/2 }   = {f₁a , f₂a+1*d/2 , f₃b}
  . . . . . . .
n=n:   {f₁a+0, f₂a+1*d/2 , . . . , f_(n+1)a+n*d/n }   = {f₁a , f₂a+1*d/2 , . . . , f_(n+1)b}
Sind alle f_j const., z.B. =1, dann folgt:
Gl.2:
a*Sum(j: f_j=1) +Sum(j: 1 * j*d/n) -Sum(j: 1)*X =0
n natürl.Zahl>1 , j=0,1,...,n
Die Summier. von 1 ergibt (n+1), die Summier. von (j*d/n)
ergibt: 1/2*n²(n+1)*d/n ,
so daß sich aus Gl.2 zur Bestimmung von X ergibt:
  a(n+1) +1/2*n²(n+1)*d/n -(n+1)*X=0 ,kürzen:
a +d/2 =X , diese Gl. für den Schwerpunkt ist unabhängig von dem Index "n" und somit auch für n→∞ gültig, also für unendl.virle Punkte zwischen a und b.

Jetzt ist noch zu zeigen, dass die bei der Teilung entstehenden unendl. vielen Punkte so dicht liegen, dass sie einer reellen Variablen zwischen a und b entsprechen.
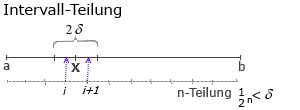
Satz 2:   , Siehe Bild zuvor
Gegeben Intervall (a-b)=d und ein reelles X , a<X<b.
Liegen in jeder δ-Umgebung U_δ(X) eines beliebigen Punktes X , a<X<b unendl.viele weitere Punkte P_i= a+i*d/n , i=0,1,...,n ,beim Grenzübergang n→∞ , dann handelt es sich bei der Menge:
Lim(i→∞: {P_i}) , um reelle Zahlen!
Beweis:
U_δ(X) bedeutet: abs(p-X)<δ ,δ>0 so vorgegeben, dass U_δ(X) ganz innerhalb des Intervalls (a,b) liegt.
Jetzt wird eine Teilung "n" so gewählt, dass (1/2ⁿ)*d<δ ist. Dann gibt es einen Index i, so dass die zwei Punkte:
P_i= a+(i/2ⁿ)*d und P_(i+1)= a+((i+1)/2ⁿ)*d , i<2ⁿ innerhalb der U_δ(X) liegen. Dann sind alle Folgepunkte:
P_ik= a+(i/2ⁿ +1/2^k )*d   kleiner P_(i+1) , für k>n .
a)   P_(i+1) -P_i = (i/2ⁿ +1/2ⁿ -i/2ⁿ)*d = d/2ⁿ <δ nach obiger Voraussetzung.
b)  Für Folgepunkte P_ik gilt P_ik<P_(i+1) :
    a +(i/2ⁿ +1/2^k)*d < a +(i/2ⁿ +1/2ⁿ)*d
=>   1/2^k < 1/2ⁿ , für k>n
c)   Beim Grenzübergang k→∞ hat man unendl.viele (Folge)Punkte in der U_δ(X).     Qed.

Diskrete Variable zu stetiger Variable:
1.   Hat man eine diskrete Folge von Punkten, so betrachtet man jedes Intervall (P_i, P_i+1) , i=0,1,...,n-2   für sich und wendet den vorigen Satz 2 an. Fazit: Jede Folge von reellen Zahlen ist zunächst eine diskrete Variable, die durch Anwendung des Satzes 2 zu einer stetigen, reellen Variablen wird.
2.   Werden die f_i mit in den Grenzübergang einbezogen, so wird aus der diskreten Funktion f() einer diskreten Variablen, eine reelle Funktion f(x) einer reellen Variablen x, im Intervall a,b.

Beispiel für Mittelpunkt f(x) , a<x<b :
Die Summenformel für Schwerpkt.X, siehe Gl.1 stellt sich in diesem Kontext wie folgt dar:
(f₀*0Δx +f₁*1Δx +...+ f_n*nΔx)
- (f₀*1Δx +f₁*1Δx +...+ f_n*1Δx)*X =0
Im Grenzübergang werden die Faktoren 0,1,2,3,... ,die den Fortschritt der Punkte P_i darstellen, zur Variablen x mit den entspr. Funktionswerten f(x), so dass man die Summen umschreiben kann: Sum(n→∞, f(x)*x) und Sum(n→∞, f(x)).
Beide Summen stellen im Grenzübergang   Δx→0, bestimmte Integrale dar:
∫[a→b, f(x)*x*dx] und   ∫[a→b, f(x)*1*dx] .
Sind alle f_i=const. z.B.=1 ,dann ist:
(1)  ∫[a→b, 1*x*dx]=   b²/2 -a²/2   und
(2)  ∫[a→b, 1*1*dx]= (b-a)
Schwerpkt.X= (b² -a²)/2= (b+a)*(b-a)/2 -(b-a)*X =0
=>   (b+a)*1/2 -1*X =0   =>  (a+b)/2 = X
Ende Beispiel

Begriffsbildung:
Elemente des Eukl.Raumes sind m-Tupel reeller Zahlen die einmal als Punkte oder als Richtungen von Null(0,...,0) aus gedeutet werden können. Symb: R^m ={p} ={(x₁,...,x_m)} ={(x₁-0),...,(x_m-0)} ,  (Koord.-Schreibweise von Pkt. und Richtung)
Aus einem allg.Pkt. p=(x₁,...,x_m) ,alle x_j≠0 kann für jede Koord. j eine Eins-Richtung e_j= x_j/Len(x_j,0) für jede Koord. (siehe Kap."6.0 Ausgangspunkt"), gewonnen werden. Werden diese Basis-Richtungen in die Punkte-Darstellung mit einbezogen, erhält man in der Koord.Schreibweise für p:
p=(x₁*e₁,...,x_m*e_m ) oder
p=(x₁*e₁ + ... +x_m*e_m ) =L(x₁,...,x_m,E)
In der Lin.-Komb. L() stehen nun die x_j als reelle Faktoren für die Basis-Richtungen e_j

Viele Punkte p_i, i=1..n , ergeben symb.:
p_i = L_i( p_i , E) in Einzel-Schreibweise:
p₁ = x_1,1 *e₁ + ... +x_1,m *e_m)
. . . . . . . . .
p_i = x_i,1 *e₁ + ... +x_i,m *e_m)
. . . . . . . . .
p_n = x_n,1 *e₁ + ... +x_n,m *e_m)
Die Add. aller p_i ergibt einen weiteren Pkt.,z.B. p, zusammengefaßt nach Koord.:
p=(a1..aj..am), Sum[i;x_i,j)]*e_j=a(j) , j=1...m
Interpretation:
1. Jedes beliebige Element, als m-Tupel oder als beliebige Lin.Komb. anderer Elemente, kann in eine normierte Lin.Komb. L() der Basis-Eins-Koord. e_j transformiert /dargestellt werden!
2. m-Richtungen in norm.L()-Darstellung können unter bestimmten Anforderungen an die Koeff. a(i,j) als neue Koord.Basis verwandt werden. (Index i steht für die m-Richt. und Index j für die m-Koord. in jeder der m-Richtungen)

m-Richtungen als Basis-Koord.:
Satz 1:
Die m-Richtungen bilden keine neue Koord.Basis, wenn sie paarweise durch Mult. mit einer reeller Zahl r ineinander überführt werden können! Symb:
non[ p(i)=r*p(j) ] oder p(i)≠r*p(j) ;∀i,j
Beweis: (indirekt)
Zum Beweis wird nur ein einziges Gegen-Beispiel benötigt. p1=(3,4) und p2=(21,28) sind in der Ebene zunächst 2 verschiedene Punkte, weil der Abstand d(p1,p2)≠0 ist.
Anderseits gilt: p2 =7*(3,4) =7*p1. Der weitere Punkt ( 1,2) läßt sich mit Lin.Komb.(p1,p2) nicht erreichen:
x*(3,4) + y*(21,28) = (1,2) ergibt Gl.System. 3x+21y=1 und 4x+28y=2
Aus Gl.2 folgt: y=(2-4x)/28 in Gl.1 y ersetzen:
==> Gl.1: 3*28x +21*(2 -4x) =1*28
==> Gl.1: 84x +42 -84x =28
==> Gl.1: 42 +0 =28 **Fehler
Fazit: Eine L(p1,p2) zu einem weitern Pkt. läßt sich nicht bilden, wegen p1=r*p2!
Ende des Beweises


Lineare Transformation /Abbildung:
Def.:   Die lin.Komb.L() von Elementen p(i) ,i=1...n des Eukl.Raumes wird als "lineare Transformation" oder lineare Abbildung" bezeichnet.
Erläuterungen zur Def.:
a) Lin.Komb.L() sind zulässige axiomatische Verknüpfungen im R^m. Deshalb: Transformation eines oder mehrerer Elemente in ein anderes Element.
b) Gleichzeitig können die beteiligten Elemente der L() als Quell-Menge und das Ergebnis als Ziel-Menge/Element bezeichnet werden. Deshalb ist L() eine Abbildung in sich.
c) Bei der speziellen 'norm.lin.Komb.L()' besteht die Quell-Menge aus den {e_j} ,j=1...m und die Ziel-Menge aus irgendeinem Punkt/Element.
d) Die lin.Komb.L() ist ein Polynom 1.Ordnung in den beteiligten Koeffizienten. Deshalb wird L() als lineare Abb. bezeichnet.
d) Die lineare Abb. besteht aus n-lin.Komb.L(), wenn die Ziel-Menge aus n-Elementen besteht, n=1,2,...

Koord.-Transformationen im R²:
Das Basis-System E={e_j} besteht aus genau m-Eins-Richtungen. Durch m-lin.Komb. mit je allen e_j erhält man eine lineare Abb. von m-Eins-Richtungen zu m-beliebigen Richtungen {p(j)}.
Speziell R²: Gl.2: p1 = a11*e1 +a12*e2 ; p2 = a21*e1 +a22*e2 .Damit {p1,p2} eine Basis bilden, müssen insbesondere die {e1,e2} jeweils als lin.Komb.L() von p1,p2 darstellbar sein.
Satz 2: In der reellen Folge {a(i,j)} ;i,j=1,2 muß die Bedingung gelten: (a(1,1)*a(2,1)-a(1,2)*a(2,1)) ≠0 , damit {p1,p2} Basis ist!
Beweis:
Gl.2 nach e1,e2 auflösen:
(1) a11*e1 +a12*e2 =p1
(2) a21*e1 +a22*e2 =p2 , -a21*e1 ,dann /a22
----------
(1) a11*e1 +a12*e2 =p1
(2) e2=(p2 -a21*e1)/a22 , e2 in Gl.(1) ersetzen
----------
(1) a11*e1 +a12*(p2 -a21*e1)/a22 =p1 , nach e1 zusammenfassen
(1) (a11 -(a12*a21)/a22)*e1 +a12*p2/a22 =p1 , a22 ausklammern
(1) (a11*a22 -a12*a21)*e1 +a12*p2 =p1*a22 ,a11*a22 -a12*a21 =D setzen
(1) e1= (p1*a22 -a12*p2)/D , e1 in Gl.(2) einsetzen
----------
(2) e2=(p2 -a21*(p1*a22 -a12*p2)/D) /a22 ,ausklammern
(2) e2=(p2*D -a21*a22*p1 -a21*a12*p2)/D) /a22 ,D einsetzen
(2) e2=(p2*a11 -a21*p1)/D
Ergeb: e1= (p1*a22 -a12*p2)/D
       e2 =(p2*a11 -a21*p1)/D
Diese Form des Ergebnis heißt 'Kramersche Regel' und funktioniert nur wenn D≠0 ist.
Jetzt muß noch bewiesen werden, daß D=0 nur (genau) dann eintritt, wenn eine Richt.das Vielfache der anderen Richtung ist.
Nach Satz1 darf a1 nicht die gleiche Richtung, wie a2 haben, oder umgekehrt.
Sei a2=r*a1, dann a2=(r*a11,r*a12) in D einsetzen:
D: a11*r*a11 -a12*r*a12 =0 (Wenn 2 Richt. gleiche Richtung haben, ist D=0).
Umgekehrt gilt: a11*a22 -a12*a21 =0 ,umformen:
Gl.(3):   a11*a22 = a12*a21 ,Skapro²(a1,a2) bilden:
(a11*a21 +a12*a22) * (a11*a21 +a12*a22)
= (a11²*a21² +a11²*a22² +a12²*a21² +a12²*a22²) ,Gl.(3):
= (a11²*a21² +a12²*a21² +a12²*a21² +a12²*a22²)
= (a11²*a21² +2*a12²*a21² +a12²*a22²) ,umformen:
= (a11²+ a11²)*(a21²+ a22²) ,=[Abs(a1)*Abs(a2)]²
==> Skapro²(a1,a2) =[Abs(a1)*Abs(a2)]² ,(Das gilt nur, wenn a1,a2 auf einer Geraden liegen, also a1=r*a2 ist. )
Ende des Beweises

Die Koord. x1,x2,... sind zunächst nichts anderes als Punkte bzw. Zentral-Richtungen. Unter diesem Kontext versteht man eine Koord.Trans. als m-dim Abb.F des linearen (x1,x2,...)-Raumes in einen ebenfalls linearen (x1',x2',...)-Raumes. Anforderung an F():
- F() umkehrbar eindeut. Funktion des gesamt. R^m in sich
- Alle Fundamental-Folgen des Quell-Raumes werden in Fundamental-Bild-Folgen abgebildet:
{p(i)}->p ,dann gilt: {F(p(i))}->F(p) ,p,p_i∈ R^m
Folgerung1:   F() und F^-1() sind stetig differenzierbar.
Folgerung2:   F() =lineare Transf. , also:
    p'= A*p ,A={a_i,j} ,(A =m²-quadr.Matrizen reell.Zahlen), dann sind Anford.gegeben und alle part. Ableitungen der m-Lin.-Komb(),=Bild-Koord., nach den Quell-Koord. existieren und sind an jedem Pkt. des Raumes R constant, nämlich =a_i,j.

Sachverhalt für nicht-lineares F():
Die Anford. an F() sind die gleichen, wie bei den Lin.-Transformationen. Unterschied sind die part.Ableitungen. Diese sind an jedem Pkt.des Raumes verschieden und selbst Funktionen der x1,x2,... :
F: {(x1..xm,x'1...x'm) , F_j(..x_j..x'_j..)=0 , j=1..m}
Erläuterungen:
Die m-Einschränkungen F_j() werden wegen Auflösungs-Theorie allg. implizit angegeben. Hier, bei unseren Koord.Transf., werden die Ziel-Koord. explizit als Funktionen der Quell-Koord. angegeben. Es existiert also i.a. bereits eine Auflösung in Richtung Quelle->Ziel:
x'_j=f_j(x1,...xm) ,j=1..m ,dann gilt:
F: {(..x..x'..) , F_j()=(...x_j...f_j...)=0 , j=1..m}
Um nach den Ziel-Koord. aufzulösen, werden für jedes f_j die part.Abl. nach x_i gebildet und ein lineares part.DGl.-System 1.Ordnung aufgestellt wie folgt:
F: {(x1..xm,y1...ym) , F_j(..x_j..y_j..)=0 , j=1..m}
y_j=f_j(x1,...xm) =>F_j: (y_j - f_j)=0
(Gl1): D_x(i)F_j() +Sum[j=1..k](D_y(i)F_j * D_x(i)f_j )
Erläuterung zu (Gl1): Für jedes x(i) gibt es ein lin.Gl.System mit m-Gleichungen(j) zur Bestimmung von
- D_x(i)f₁,. . ., D_x(i)f_m
- Die m²-Koeff. der m-lin.Gl.Systeme (Gl1(i)) sind immer gleich, nämlich {D_y(i)F_j}. Daraus folgt für lineare F()-Funktionen part.Abl., die überall im Raum const. sind , und für nicht-lin. Funktionen part.Abl., die eine Funktion der Ort-Koord. im Raum darstellen. Die zugehörigen Determinanten sind bei lin.F() überall =const. und sonst eine sogenannte Funktional-Determinante, symb.: Det() =D(F1...Fm)/D(x1...xm)
Definition:
- Funktion() =Abb.von Elementen des R^m in den R¹
- Funktional() =Abb.von Objecten des R^m in den R¹
Bemerkung:
Die Behandlung über ein solches Gl.System klappt auch bei nicht-lin. funktionellen Zusammenhängen deshalb, weil die Differentiale Richtungen in die einzelnen Koord.-Funktionen darstellen, und die Richtungen selbst über Linear-Kombinationen mit einander verbunden werden (siehe auch totales Diff.).

Beispiel für Vorgehensweise an Hand lin.Koord.-Transf.,(lineares F()), in der Ebene:
a(1,1)*x +a(1,2)*y = u   (F1=(-u + a11*x +a12*y)=0 )
a(2,1)*x +a(2,2)*y = v   (F2=(-v + a21*x +a22*y)=0 )
u=u(x,y) , v=v(x,y) , = lineare Funktionen von x,y
Vorbemerkungen:
1.   Es handelt sich im Beispiel, abstrakt betrachtet, um eine eingeschränkte Abb. im R²⁺². Zunächst sind die 4 reell. Variablen (x,y,u,v) unabhängig, bilden also einen kompletten 4-dim Raum ab. Durch die 2 Gleichungen u=f1(x,y) , v=f2(x,y), wird der R⁴ i.a. auf einen 2-dim Unterraum eingeschränkt. Dabei ist es egal, ob die zugehörigen Koord. des Unterraumes von (x,y);(x,u);(y,u);(u,y) usw. gebildet werden.
2.   Für unsere Koord.Trans. ist nur entscheidend, daß die F1,F2 im gesamten Raum stetig differenzierbar sind nach allen Variablen.
Abb.F: {(x,y,u,v) , F1(x,y,f1,f2)=0 , F2(x,y,f1,f2)=0 }
Die Vorwärts-Auflösung ist gegeben, so daß wir hier rückwärts, nach x,y auflösen, unter Berücksichtigung, daß u,v jetzt unabhäng.Variablen sind und x=x(u,v) und y=y(u,v) Funktionen darstell.:
(1)   D_uF1 +D_xF1* D_f1x +D_yF1* D_f1y =0
(2)   D_uF2 +D_xF2* D_f1x +D_yF2* D_f1y =0
(1a)   D_vF1 +D_xF1* D_f2x +D_yF1* D_f2y =0
(2a)   D_vF2 +D_xF2* D_f2x +D_yF2* D_f2y =0
----------------------
D_uF1= -1 , D_uF2= 0 , D_vF1 = 0 , D_vF2= -1
(D_xF1, D_yF1, D_xF2, D_yF2) = (a₁₁, a₁₂, a₂₁,a₂₂)
(1)+(2) und (1a)+(2a) sind jeweils lin.Gl.Systeme zur Bestimmung der (fett)-Variablen(part.Abl.):
(1)  -1 +a11* D_f1x +a12* D_f1y =0
(2)   0 +a21* D_f1x +a22* D_f1y =0
--------------D= a11*a22 -a12*a21 ---------
(1a)   0 +a11* D_f2x +a12* D_f2y =0
(2a)  -1 +a21* D_f2x +a22* D_f2y =0
Lösung nach Kramer'scher Regel, siehe Abschnitt zuvor:
D_f1x= (1*a22 -a12*0)/D = a22/D
D_f1y =(0*a11 -a21*1)/D = -a21/D
D_f2x= (0*a22 -a12*1)/D = -a12/D
D_f2y =(1*a11 -a21*0)/D = a11/D
part.DGl. sind constant, daraus folgt:
x= a22/D *u -a12/D *v   =( a22*u -a12*v)/D
y= -a21/D*u +a11/D*v   =(-a21*u +a11v)/D
(partikuläre Lösungen werden zusammengewfaßt! , Ende Beispiel)

Im folgenden Abschnitt wird das gleiche Beispiel für ein nicht lin. F() im R²⁺² durchgerechnet (Polar-Koord.-Transformation).

Beispiel "Polar-Koordinaten":
Polar Koord. werden i.a. durch die Rückwärts-Abbild. zu den karth.Koord. definiert:
p=(x,y)= (r*cos(t), r*sin(t)) = r*(cos(t), sin(t))
Der allg.Punktes p wird jetzt als Zentral-Richtung w=(p-Null) gedeutet,mit folg. Eigenschaften:
- Richtung in der Ebene =Winkel zu x-Koord.
- Len(w) =±Länge von w auf Gerade (p,Null)
Beide Eigenschaften werden den unabhängigen reellen Zahlen t,r zugeordnet, so daß die zugehörige Abb.F im R²⁺² lautet:
Abb.F: {(x,y,r,t) , (x -r*cos(t))=0, (y -r*sin(t))=0 }
Eigenschaften von F():
a)   In der gegebenen Auflösung nach x=x(r,t) und y=y(r,t) erkennt man sofort , daß es sich um eine 1 zu 1 Abbildung handelt, d.h.,ist p=(x,y) und p'=(r,t), so sind diese Punkte identisch, wegen:
p-p' = (x-r*cost,y-r*sint) =(0,0) (wenn man für x,y = x(),y() einsetzt).
b)   Die lineare Abb. x=u und y=v ist ebenfalls eine 1 zu 1 Abbild. Später wird gezeigt, daß x=r*cos(t) und y=r*sin(t) die einzige nicht-lin.-(1 zu 1)-Koord.-Transformation in der Ebene ist
c)   Betrachtet man die Abb.-Folge: (r,t) ->r*(f1,f2) ->(x,y) so fällt auf, daß f1,f2 =cos,sin zyklische Funktionen der reellen Variablen t sind, d.h. cos(-t)=cos(t) und -sin(-t)=sin(t). Der Zyklus-faktor ist 2pi.
Polar-Koordinaten:   Der Punkt w in x,y-Koord. und w' in rcost,rsint-Koord. ist gleich (nach Koeff.Vergleich!), also 1 zu1 Abbildung.
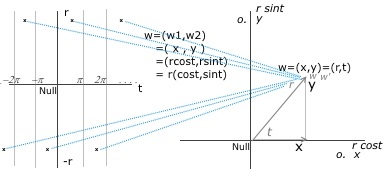
Auflösung nach r=r(x,y) und t=t(x,y):
Abb.F: {(x,y,r,t) , (-x +r*cos(t))=0, (-y +r*sin(t))=0 }
(1)   D_xF1 +D_rF1* D_xr +D_tF1* D_xt =0
(2)   D_xF2 +D_rF2* D_xr +D_tF2* D_xt =0
(1a)   D_yF1 +D_rF1* D_yr +D_tF1* D_yt =0
(2a)   D_yF2 +D_rF2* D_yr +D_tF2* D_yt =0
----------------------
D_xF1=-1 ; D_xF2=0 ; D_yF1=0 ; D_yF2=-1
Funk.Det():
(a11) D_rF1=cos(t) ; (a12) D_tF1=-r*sin(t)
(a21) D_rF2=sin(t) ; (a22) D_tF2=r*cos(t)
D(a₁₁a₂₂-a₁₂a₂₁): r*(cos²(t) +sin²(t)) =r
-------lin.-part.-DGl.-------
(1)   a11* D_xr +a12* D_xt =1
(2)   a12* D_xr +a22* D_xt =0
(1a)  a11* D_yr +a12* D_yt =0
(2a)  a21* D_yr +a22* D_yt =1
----------------------
Lösung nach Kramer'scher Regel:
D_xr= (a22*1 -a12*0)/D = cos(t)
D_xt= (a11*0 -a21*1)/D =-sin(t)/r
D_yr= (a22*0 -a12*1)/D =-sin(t)
D_yt= (a11*1 -a21*0)/D = cos(t)/r
Ansatz: Es gilt (D_xr)² +(D_yr)² =1, setzt man r²=x²+y², so ergeben die part.Ableitungen:
(1):  2*r*D_xr =2x   => (D_xr)²= x²/r²
(1a): 2*r*D_yr =2y   => (D_yr)²= y²/r²
Werden beide Gleichungen addiert, so folgt: (x²+y²)/r² =1.
D_xt/D_yt = -sin(t)/cos(t) = -y/-x =y/x => t=arttan(y/x)
Ende Beispiel

Eigenschaften von cos(t) und sin(t):
1.   f=cos(t), g=sin(t). Aus F= f²+g²=1 folgt:
D_tF: 2*f*D_tf +2*g*D_tg =0   => f*D_tf = -g*D_tg
Durch Koeff.Vergleich folgt: D_tf =-g und D_tg= f ,also:
    D_tcos(t)= -sin(t) und  D_tsin(t)= cos(t)

2.   Variable t beginnt bei 0 im Pkt.(1,0) => cos(0)=1 , sin(0)=0 . t folgt den Punkten auf der Kreislinie und gibt die Differenz-Bogenlänge d zwischen (1,0) und akt.Pkt.(x,y) in pos.Richtung wieder:
d= Bg((x,y) -(1,0)). Alle 2pi zeigt t wieder auf Anf.(1,0). Daraus folgt: Aus t kann man Anz.Umdrehungen ermitteln.

3.   Beziehungen zwischen cos() und sin(): Bildauswertung:
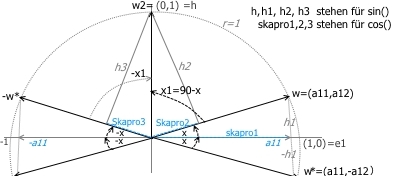
h1= (e1 x w)= (1*a12-0*a11)= a12= sin(x)
h= w2= (e1 x w2)= (1*1-0*0)= sin(90°)=1
h2= (w x w2)= (a11*1-a12*0)= a11= sin(x1)
h3= (-w* x w2)= (-a11*1 -a12*0)= -a11=sin(-x1)
[ h2,h3 ergeben:   sin(-x1)= -sin(x1) ]
Skapro1= (e1*w)= 1*a11 +0*a12)= a11= cos(x)
Skapro2= (w*w2)= a11*0 +a12*1)= a12= cos(x1)
Skapro3= (-w* *w2)= (-a11*0 +a12*1)= a12= cos(-x1)
[ Skapro2,3 ergeben:   cos(-x1)= cos(x1) ]
Durch ganze Drehung des Bildes (360°~ 2pi) ergibt sich wieder das Ausgangsbild. Daraus folgt:
cos() und sin() sind zykl.Funktionen mit Periode 2pi .
cos() und sin() sind ident.Funkt., nur um 90° versetzt:
      sin(x) = cos(90-x) ; cos(x) = sin(90-x)
cos() ist gerade Funktion, wegen cos(-x1)= cos(x1)
sin() ist ungerade Funkt. , wegen sin(-x1)= -sin(x1)

Die wichtigen Add.Theoreme für cos(a±b) und sin(a±b) werden am folg. Bild erläutert:
Bildauswertung:
Die Höhen h,h1 stehen im Eins-Kreis für den sin() der Zentralwinkel, die s,s1-Strecken = Abschnitte zwischen Höhen h,h1 und Pkt.Null für den cos() der Zentralwinkel. Die Höhen berechnen sich über die Flächen-Produkte F(), die Strecken s,s1 über die Skalarprodukte.
h= F(w* x w2)= (a11a22 +a21a12)= sin(x+x1)
    = cos(x)sin(x1) +cos(x1)sin(x)
h1= F(w x w2)= (a11a22 -a21a12)= sin(x-x1)
    = cos(x)sin(x1) -cos(x1)sin(x)
s,s1 =Skapro():
s= (w* *w2)= a11a21 -a12a22= cos(x+x1)
    = cos(x)cos(x1) -sin(x1)sin(x1)
s1= (w * w2)= a11a21 +a12a22= cos(x-x1)
    = cos(x)cos(x1) +sin(x1)sin(x1)

1. Spez.Potenz-Reihen:
Im "Modell der reellen Zahlen ;Kap.3.3: Beispiele für konvergente Folgen" hatten wir Potenz-Reihen für reelle Zahlen x wie folgt gebildet:
P_n(x)= x⁰ +x¹ +x² ... +xⁿ     Dies sind zunächst Polynome und man erhält die Summe zu: (xⁿ⁺¹ -x)/(x-1)
Beim Grenzübergang n->∞ erkennt man sofort, daß für Abs(x)≥1  P_∞(x) nicht konvergiert, sondern nur für Abs(x)<1, dann ist Lim(xⁿ)=0.
Satz1:    Die Potenzreihe P(x)= x⁰ +x¹ +x² +x³ + ... konvergiert für Abs(x)<1, der Grenzwert beträgt: x/(1-x) .

2. .Allg. Potenz-Reihen:
Setzt man für x=(a*x1), dann konvergiert:
(1)  P_n(x1)= (a*x1)⁰ +(a*x1)¹ +... +(a*x1)ⁿ , für n->∞, entspr. Pkt.1 zuvor ebenfalls nur für Abs(a*x1)<1 . Aus dieser Ungleichung erkennt man sofort, daß diese (Ungleichung) auch für weitere "x" gilt, nämlich: ∀x , Abs(x)<x1 .
Setzt man in Potenzreihe(1):  a_j=a^j , j=0,1,2... ,so konvergiert P(x) für das vorgegebene x1, wenn Abs(a*x1)<1 ist, und damit für alle x: Abs(x)≤Ab(x1).
In diesem Kontext wird Ab(x1) als "Konvergenz-Radius r" einer Potenzreihe bezeichnet!

Def.:  Die allg. Potenzreihe P(x)= a₀x⁰ +a₁x¹ +a₂x² + ...
hat den Konv.Radius r, wenn Abs(a^1/j)<(1/r) ist.
Beispiel: Sei a_j=0.5^j , dann folgt aus Abs(0.5*x)<1: x<0.5
Folgerung.:  Die allg. Potenzreihe ist auch eine Funktion im offenen Intervall: -r<x<r
Folgerung.:  Die allg. Potenzreihe wird von der Koeff.Folge {a_j} eindeutig festgelegt. Das bedeutet: Über die Potenzreihen-Entwicklung einer Zahlen-Folge {a_j}, j=0,1,2,... wird eine Funktion eindeutig bestimmt =abgebildet im Quell-Intervall Abs(x)<r.
Die Potenzreihen-Entwicklung ist deshalb ein Funktional, also Abbildung eines (Eukl.)Objektes in den Eukl.Zahl-Raum, und die Def. einer Funktion über eine P()-Entwicklung eine sogenannte Funktional-Gleichung.

Satz2:    f(x) sei eine Funktionen-Reihe mit Koeff.Folge {a_j} und Konv.Radius r und {á_j} eine weitere Folge. Dann bildet die Potenzreihe: á₀x⁰ +á¹x¹ +á²x² + ... ebenfalls eine Funktionen-Reihe mit nicht kleinerem Konv.Radius r, wenn Abs(á_j)<Abs(a_j), ∀j ist.     Beweis:  Die Richtigkeit der Aussage leuchtet sofort ein.
Folgerung:  Satz2 gilt auch für die Koeff.Folgen {á_j} mit:
Abs(á_j)=Abs(a_j), ∀j j>m ,m natürliche Zahl.
Beweis:  Für die ersten (m+1)-Summanden setzen wir: á_j=(a_j-b_j) , j=0,1..m. Dann bilden wir die Funk.Reihen f und g:
f(x)= a₀x⁰ +a₁x¹ +a₂x² +...
g(x)= (a₀-b₀)x⁰ + .... +(a_m-b_m)x^m
        + a_m+1x^m+1 + a_m+2x^m+2 + a_m+3x^m+3 +...
     = -(b₀x⁰ + ... +b_mx^m)
       + a₀x⁰ + a₁x¹ + a₂x² +...
g(x) aufspalten in: g(x)= g°(x) + f(x). Dann sind g°(x) die ersten (m+1)-Summanden und ergeben im gesamten Konv.Radius einen endlichen Wert: Abs(g°(x))≤k , k>0, ∀x Abs(x)<r .
So gilt: wenn f(x) konvergiert, dann konvergiert auch f(x)+k im gleichen Intervall.
Ende des Beweises

3. Stetigkeit von f im offenen Intervall:
f(x) konvergiert nur innerhalb des Konv.Radius, ist also auch nur hier, Abs(x)<r ,stetig.
Sei M ein kompaktes Intervall in U(r), also M⊂U(r).
Dann gilt für die Eigenschaften von f in M:
a) f ist beschränkt in M
b) zu jedem Pkt. x∈M gehört auch eine ganze U_δ(x) zu M. Wegen f=beschränkt gehört auch U_ε(f(x)) zu M.
c) Damit wird jede Fundamental-Folge in U_δ(x) in eine entspr. Fundamental-Folge in U_ε(f(x)) abbgebildet. Es können somit zu jedem Pkt.x∈M Differential-Quotienten Lim(Δf(x)/Δx ) ermittelt werden.
d) f ist in M beliebig oft differenzierbar.

Problem: Gibt es eine Folge {á_j} deren Konv.Radius ≥r (r>0 beliebig) ist?
Lösung: Entspr. Folgerung zu Satz2 gilt: Jede Folge {á} ,deren Elemente ab einem Index m der Ungleichung: á_j<a_j , j>m genügen, ist die Folge mit beliebigen Konv.Radius r!

Satz3:    {á_j} , á_j=1/Fak(j) ist die gesuchte Koeff.Folge.
Beweis:  n!>aⁿ für n≥ a(a+1)
Zur genauen Beweisführung siehe Textblock am Kap.Ende!

4. Exponential-Funktion exp(x):
Die Funktionalgleichung der exp(x) -Funktion lautet:
exp(x)= e^x = 1/0!*x⁰ +1/1!*x¹ +1/2!*x² +...
Der Konvergenz-Radius r umfaßt somit alle Konv.Radien aller mögl. Potenz-Reihen, r>0 beliebige reelle Zahl.
Bemerkung   Der Konv.Radius bei Potenz-Entwicklungen Zyklischer Funktionen ist unendl.!
Die wichtigste Eigenschaft der exp() ist die DGl.: D_xexp(x)= exp(x).

5. Potenz-Reihen-Entwicklung:
Ist eine Funktion f(x) beliebig oft differenzierbar in einem Radius Abs(x)<r so kann man die Koeffizienten einer mögl.Potenzreihe wie folgt bestimmen:
f(x)= a₀x⁰ +a₁x¹ +a₂x² +...
Die Ableitungen von f(x) nach x bezeichnen wir in der Folge symb.: f'(x)
Dann gilt: f(0)= a0, f'(0)= a1/1, f''(0)= a2/2, .....
und: f(x)= f(0)*x⁰ +f'(0)*x¹ +f''(0)*x² +...
Diese Form heißt: "MacLaurin'sche Form" der Potenzreihen-Entw.

Da die zykl Funktionen cos() und sin() ebenfalls unendl.mal differenzierbar sind, kann man für sie ähnliche Potenzreihen entwickeln.

Für die Ableitungen von cos und sin gilt:
D_tcos(t)= -sin(t) und  D_tsin(t)= cos(t)   Siehe Kap.6.4 zuvor: 'Eigenschaften von cos(t) und sin(t)' !
Daraus können die Funktions-Werte im Pkt.0 ermittelt werden:
f1=cos(), f2=sin(),   Ableit.im Pkt.0:

      cos   sin   Tang.im Pkt
f¹'    0     1     f1,f2 +0°
f²'   -1     0     f1,f2 +90°
f³'    0    -1     f1,f2 +180°
f⁴'    1     0     f1,f2 +270°
----------------------------
f⁵'    0     1     f1,f2 +0°
f⁶'   -1     0     f1,f2 +90°
... weiter wie oben
Daraus können jetzt die Koeff. für die Potenzreihe bestimmt werden:
       cos     sin
a0:    1/0!    0/0!   (f⁰'(0))
a1:    0/1!    1/1!   (f¹'(0))
a2:   -1/2!    0/2!   (f²'(0))
a3:    0/3!   -1/3!   (f³'(0))
a4:    1/4!    0/4!   (f⁴'(0))
a5,a6,a7,a8 wie a1,a2,a3,a4 usw.
Potenzreihe:
(1) cos= 1 +0*x¹ -1/2!*x² + 0*x³ + 1/4!*x⁴ +...
(2) sin= 0 +1*x¹ +0/2!*x² -1/3!*x³ +0/4!*x⁴ +...

Wir lösen uns jetzt vom (x,y)-Koord.System und gehen von einer unabhäng.reellen Variablen t aus. Die Menge M={t} ist äquivalent zu einem R¹. Das zugehörige Eins-Element sei "e". Die Elemente p von M können wie folgt beschrieben werden:
p= (t)= t    Koord.-Schreibweise
p= t*e        Richtungs-Schreibweise
Die Funktional-Gleichungen für die Potenz-Entw. von t*e lauten:
w1= cos(te)= 1 +0*(te)¹ -1/2!*(te)² + 0*x³ ..
w2= sin(te)= 0 +1*(te)¹ +0/2!*(te)² -1/3!*(te)³ ..
Wenn man jetzt axiomatisch festlegt: e²=-1 und w1+w2 bildet, erhält man eine Potenz-Reihe für exp(t*e):
1 +1*(te)¹ -1/2!*(te)² -1/3!*(te)³ +1/4!*(te)⁴ +1/5!*(te)⁵ +...
=   1 +1*t¹e +1/2!*(t)² +1/3!*(t)³e +1/4!*t⁴ +1/5!*t⁵e +1/6!*t⁶ +...
Die nicht unterstrichenen Summanden bilden die cos-Reihe, die unterstrichenen Summanden die Reihe: sin(t)*e
Def.:   Um Verwechslungen mit den normalen Eins-Elementen zu vermeiden, bezeichnet man "e" als "i" (i= imaginäre Einheit).
Folgerung:   Zwischen Potenzreihen (1), (2) und (w1+w2) besteht folg. Beziehung:
cos(t) +i*sin(t)= exp(it)     Funktional-Gleich. der komplexen Zahlen !

Bemerkung:   Mit w=(w1,w2)= w1+i*w2= e^it wird ein Element des R² festgelegt, also eine Eins-Richtung um Pkt.Null w=(w-0), Abs(w)=1. "w" ist dabei ein Bild eines reellen Parameters t, der durch 2 Funktionen f1,f2 in 2 reelle Ziel-Variable w1=f1(t), w2=f2(t) transformiert wird:
{(t,r,w1,w2) F= f1²+f2²-r²=0, f1(t),f2(t) }.   Hier ist f1,f2 mit r mult.
Dies ist eine Abb. im R²⁺², deren Einschränkung als Bild-Menge eine 2-dim Kurve (Kreislinie) liefert, die durch die weitere reelle unabhängige Variable r durch den ganzen R² gezoomt wird.
Insgesamt stellt F() eine 1 zu 1 Abbild. des R² in sich dar, d.h., die Koord. (f1,f2) im äquivalenten kompl.R² sind wertmäßig die gleichen wie im reellen Zahlraum R²!

Folgerung:   Beide Räume (reell.,kompl.) entstehen durch Funktionen von 2 reellen Quell-Variablen, symb.: t, s , ,wie folgt:
reell.R²: {(t,s, x,y) F=(f1,f2), z.B.: x=t,y=s}, f1,f2 identische Fkt.
kompl.R²: {(t,s, x,y) F= f1²+f2²-s²=0, f1(t),f2(t)}, f1,f2 zykl.Funkt. von t mit Kreisfrequenz 2pi.
Die Umkehr-Funktionen sind dabei nur im reell.R² eindeutig (identisch). Im kompl.R² nur eindeutig bezüglich einer ±Windungszahl (Vielfaches von 2pi). Die Windungszahl wird dabei durch die Quell-Variable t festgelegt.
Rückwärts, von kompl.->reell., kann nicht mehr auf die Windungszahl geschlossen werden.

Folgerung:   Ist f2=0, z.B. durch t=0, mutieren die kompl.Zahlen zu reellen Zahlen. Das bedeutet, man kann zunächst nur mit einer Teilmenge von {w} rechnen (=axiomat.Verknüpfungen im R¹).
Da die Zahlen w, wie auch reelle x, durch Potenzreihen beschrieben werden, mit denen man rechnen kann, liegt die Vermutung nahe, daß man auch mit allen Elementen (f1,f2) rechnen kann! Dies erfordert den Nachweis aller Verknüpfungen, wie sie im reellen Zahlraum möglich sind.

Def.:   Mit w= exp(it) wird ein Element des R², also eine Eins-Richtung um Null, (w-0), Abs(w)=1, beschrieben.
Multipliziert man w mit einer reellen Zahl r, so dient r als Zoom-Faktor für w und erreicht damit jeden Punkt der Ebene, symb.: p=r*w ∈R². Zur Unterscheidung von p zu reell.Zahl schreiben wir statt p "z".

Die Menge der kompl.Zahlen {z} ist mit der Menge aller 2-Tupel reeller Zahlen {(x,y)} gleich, bezüglich des Koord.Vergleiches eines Punktes p=(x,y) in beiden Mengen! Alle Elemente können über Potenzreihen beschrieben werden.

Funktionalgleich. für z :   cos(z) +i*sin(z)= e^iz
e^iz= e^ix*e^i*iy =  (cos(x)+i*sin(x)) * (cos(iy)+i*sin(iy))
=  cos(x)cos(iy)-sin(x)sin(iy) + i (sin(x)cos(iy)+cos(x)sin(iy))
Nach Add.Theorem f. cos/sin 6.4a gilt:
cos(x)cos(iy)-sin(x)sin(iy) = cos(x+iy)
sin(x)cos(iy)+cos(x)sin(iy) = sin(x+iy)
zusammen also:
e^i(x+iy)= cos(x+iy) +isin(x+iy)   Beweis Ende

Verknüpfungen in {z} (kompl.Zahlen):  
- Add./Sub. entspr. linearer Eigenschaft des R²
- Mult: z1*z2 , d1= Abs(z1), d2= Abs(z2)
=>  z1= d1e^it1, z2= d2e^it2, z1z2= d1d2e^i(t1+t2)
e^i(t1+t2)= cos(t1+t2)+i*sin(t1+t2)
Nach Add.Theorem f. cos/sin 6.4a gilt:
= cos(t1)cos(t2) - sin(t1)sin(t2) +i (sin(t1)cos(t2) + cos(t1)sin(t2))
d1,d2 hinein multipl.:
= d1cos(t1)*d2cos(t2) - d1sin(t1)*d2sin(t2)
    +i (d1sin(t1)*d2cos(t2)+ d1cos(t1)*d2sin(t2))
Die Faktoren sind Koord.von z1,z2:
=> x1x2 -y1y2 +i (y1x2 +x1y2)= z1*z2

- Div: z1/z2 , d1= Abs(z1), d2= Abs(z2)
=>   z1/z2= d1/d2 e^i(t1-t2)
Nach Anwendung der Add.Theorem für cos(a-b)/sin(a-b) 6.4a gilt für e^i(t1-t2):
= cos(t1)cos(t2) + sin(t1)sin(t2) +i (sin(t1)cos(t2) - cos(t1)sin(t2))
d1*d2/d2*d2 hinein multipl.:
=1/d2² *d1cos(t1)*d2cos(t2) + d1sin(t1)*d2sin(t2)
    +i (d1sin(t1)*d2cos(t2)- d1cos(t1)*d2sin(t2))
Die Faktoren sind Koord.von z1,z2:
=> 1/d2² *(x1x2 +y1y2 +i (y1x2 -x1y2) )= z1/z2

Die Verknüpfungen sind i.a. wieder kompl.Zahlen, so daß die Frage: "Wann ist die Add() und Mult() von z1,z2 eine reelle Zahl?" zu einer besonderen Zahl z* führt:
Add.: (x1+iy1)+(x2+iy2)= x1+x2 +i(y1+y2)
Mult: (x1+iy1)*(x2+iy2)= x1x2-y1y2 +i(y1x2+x1y2) oder:
    : r1e^it1*r2e^it2= r1r2e^it1+it2
=> wenn beide Zahlen im Im[] gleich sind, bis auf das Vz., dann ist das Ergebnis eine reelle Zahl!
Add.: y1=-y2 => = x1+x2 +i(y1-y1)= x1+x2 +i0
Mult: (y1x2+x1y2)=0 => y1x2=-x1y2 => y1=-x1y2/x2
    : x1x2 +x1y2²/x2 +i0
Folgerung1: Ist x1=x2, dann liegen z1,z2 symmetrisch zur reellen Koord.Achse mit gleicher Len().
Add() ergibt 2x und Mult() x²+y².
Def.: Die zu einer kompl.Zahl symmetr. liegende Zahl mit gleicher Len() heißt: "konjugiert-kompl.Zahl", symb.: z*, wobei gilt: (z*)*=z .
Folgerung2: Rechnen mit z und seiner konj.kompl.Zahl z*:
z= x +iy , z*= x-iy
Mult: zz* = xx-y(-y) +i( x(-y) +yx) = x²+y²
     = Skapro(z,z)= Len²(z)
Add: z+z*= x+x +i(y-y )= 2x .Umgekehrt kann man aus jeder reellen Zahl eine Kombination aus kompl. +konj. kompl.Zahl machen:
z=(a, b)   => a= 1/2*(z+z*) !  (Diese Umwandlung wird im Pkt.6.11: "part. kompl. Diff.Quotienten der kompl.Funktion f bezuüglich 'z' bzw. 'z*'" genutzt)

Folgerung3: Es gibt genausoviele kompl.Zahlen, wie konj. kompl.Zahlen.

- Abstand zweier Zahlen d(z,z1):
d²(z,z1)= (z-z1)(z-z1)* ,ist insbesondere z.B. z1=0, dann ist d(z,0)= sqrt(zz*) die Länge der Richtung von Null->z oder Abs(z). (oder: re^it *re^i-t= r²)

- Koord. in Richtung z:
z= re^it/r ist eine Eins-Richtung in Richtung z und könnte damit als eine erste Basis-Richtung e1° für {z} gelten. Die zweite Basis-Richtung e2° wird durch:   D_te^it= i*e^it gebildet.
e1°= e^it , e2°= i*e^it
e1°= cost +i*sint , e2°= -sint +i*cost
Eigenschaften von (e1°,e1°):
- Skapro()= -cost*sint +sint*cost= 0   Orthogonal
- F(e1°,e2°)= cos²t -(-)sin²t= 1 Orthonormiert (Rechts-System)
Folgerung:  Die Koord. sind bezügl. (e1,e2) oder (1,i) nicht fest, sondern bewegen sich mit der akt.Richtung von "z".

- Funktionen/Abbildungen in z:
Eine kompl.Funktion F() bildet den R² in den R² ab.
f1= Re[F], f2= Im[F], also F= f1+i*f2 :
{(z,u) F= f1 +i*f2, u1=f1(z), u2=f2(z) } ,F dreht, staucht o.verlängert die Richtungen der Ebene.
Spez.Fall: z=(t,r), f1²(t)+f2²(t) -r²=0 .Hier ist F=(f1,f2) eine (die) 1 zu 1 Abbildung der Ebenen-Punkte in sich.
Spez.Fall: z=(t,0), Hier bildet F= f1 +i*f2 eine reelle Variable in die kompl-Ebene ab.

Nachfolgend sei M kompaktes Intervall und C⁽ⁿ⁾(M) sei Menge der in M  n-mal stetig differenzierbaren Funktionen (differenzierbar nach Variablen-Koord.Richtungen in M).
D⁽ⁿ⁾f(x°)= f_°^n' sei n-te Ableitung von f in Pkt.x°.

Potenzreihen-Entw. diff.barer Funktionen:
x,x°∈M , f(x)=f(x)= a₀(x-x°)⁰ +a₁(x-x°)¹ +...+a_n(x-x°)ⁿ
=> f ist Polynom und damit diff.bar u. somit f∈C⁽ⁿ⁾(M)
Nach Kap.6.5 zuvor können die Koeff. a(j) zu:
a(j)= 1/j!*f₀^n' bestimmt werden. =>
f(x)= 1/0!*f₀^0'(x-x°)⁰ +1/1!*f₀^1'(x-x°)¹ +..
     +1/(n-1)!*f₀^(n-1)'(x-x°)^n-1 +
     +1/n!*f(x~)^n'(x-x~)ⁿ
Dies ist die Taylor'sche Form der Potenzreihen-Entw.   x~ ist nach Quotienten-Mittelwert-Satz existierender Zwischenwert in M .
1/n!*f(x~)^n'(x-x~)ⁿ  heißt Restglied n-ter Ordnung R(n).
Man könnte M auch hier als Umgebung von x° betrachten.
Beispiel:
f(x)= 1/(1+x) +x² , 0≤x≤2 , x°=1
D¹f= -1/(1+x)²+2x , D²f= 2/(1+x)³+2 , D³f= -6/(1+x)⁴
f(1)= 3/2 , Df(1)= 7/4 , D²f(1)= 9/4 , D³f(1)= -6/16
P2()= 3/2 +7/4*(x-1) +9/4*(x-1)²
Abschätzung R(3):
Wegen 1+x≥1 ist 1/(1+x)≤1 und Abs(D³f)≤6
Abs(f-P2) ≤Restglied() ≤1/3!Abs(x-1)³ *6 =Abs(x-1)³
Ergeb.: wenn die x nahe bei x°=1 liegen, also z.B. ∀x: Abs(x-1)<0.01 , dann ist der Abstand von f zum Polynom P(2), für diese x, <0.01³.

Mittelwertsatz der Diff.-Rechnung:
2-Punkte-Gleichung einer Geraden:
f(x)-f(b)= (f(a)-f(b))/(a-b) *(x-b)  =Gerade durch f(a) und f(b) , a,b∈M
Sei: Δf= f(a)-f(b) ,Δx= a-b .Dann ist Δf/Δx= k überall in M gleich, nämlich const. Dann gilt auch:
Lim(a->b; Δf/Δx)= f'(b)= k  (Man kann also beliebige Grenzübergänge bilden in M )
f geht durch a,b, aber keine Gerade:
Satz1:   f∈C⁽¹⁾(M). Ist Df in einer U_δ(x°) ,x°∈M, const., dann ist Df in ganz M const., und somit lineare Funktion (auch f=const.).
Beweis(indirekt):   Wenn das nicht stimmt, dann wäre der rechts-seitige Diff.Quotient und der links-seitige Diff.Quotient in den Randpunkten der Umg.(x°) verschieden, also f in diesen Punkten nicht differenzierbar, was aber im Widerspruch zu f∈C⁽¹⁾(M) steht!
Satz2:   Df()=k, in mind. 1 Punkt von M!
Beweis:   1. Ist f= linear, dann Qed.
2. Ist f(a)>f(b), dann a,b vertauschen (jetzt f(b)>=f(a)). Sei Df(a)=k1, Df(b)=k2:
a) Liegt k zwischen k1 und k2, dann OK, weil Df stetig von k1<->k2. Qed.
b) Sind k1,k2 < k oder >k , dann sei Df(x~)=k~ für a<x~<b . Angenommen, es gibt keinen Pkt.x~ mit Df(x~)>k o. <k, dann wäre f(x~) in Pkt.b <f(b) o. >f(b). Dies ist aber ein Fehler, da f(x~)=f(b) in x~=b sein muß! Also gibt es ein k1~ mit k1~>k o. k1~<k . Somit triit Fall 2a) ein, Qed.
Ende des Beweises

Beispiel zum Mittelwertsatz:  
f=x³-2x, Df=3x²-2, a=2, b=4, f(a)=4, f(b)=56, Df(2)=10, Df(4)=46
(1) f(x)-f(b)= ((f(a)-f(b))/(a-b) *(x-b)   2-Punkte-Geraden-Gl. durch f(a) und f(b)
Der Diff.Quotient: Δf=((f(a)-f(b))/(a-b)=k =-52/-2= 26 .
Anderseits ist das Näherungs-Polynom P₁(f) (nach Taylor):
(2) f(x)-f(b)= Df(b) *(x-b) +Restglied
Gesucht wird ein Pkt. x~ mit Df(x~)= 3(x~)²-2=k =26
=> x~=sqrt(28/3)= 3,055 . Probe: Df(3.055)=25,99
Ende Beispiel
Def:   Gl.(2) ist auch eine lineare Funktion und heißt "Linearisierung L(f) im Punkt (b,f(b)).
Im Beispiel hat L(f(x~)) den gleichen Anstieg wie Gerade (1), nämlich k=26, was dem Mittelwertsatz entspricht.

Partielle Diff.-Quotienten:
Jetzt sei f stetige Funktion in M={(x1,..x_j...xm)} =R^m
Es wird die j-te Variable betrachtet, all anderen (m-1)-Variablen sind jetzt Parameter.
Def:   Existiert der Diff.Quotient: Δf(...x_j..)/Δx_j in allen Punkten (...x_j...), so heißt f(x1..xm) partiell differenzierbar in Richtung x_j, symb: D_jf.
Dabei gilt für den Grenzübergang h->0 in einem Punkt x° in Richtung-j:
f(... x_j°+h ...)- f(x₁°.... x_m°)) /(x_j -x_j°)= D_jf(x°)
Def:   Der Zähler im Quotienten links wird allg.als Differential von f, symb.: Δ_jf (Richtung-j) und der Nenner als Differential in der x_j-Variable Δx_j bezeichnet. Den Diff.-Quotienten kann man auch als Quotient 2-Differentiale die in einem Pkt. zusammenhängen betrachten:
Δ_jf/Δx_jf= D_jf(x°)
Den Diff.Quotienten kann man wieder als Anstieg einer Geraden durch (x°,f(x°) werten, welche die Form einer 2-Punkte-Gl. hat: a=x_j, b=x_j°:
(3)  f(x)-f(x°)= D_jf(x°)*(x_j -x_j°)   2-Punkte Geraden-Gl.
Gl.(3) ist Linearisierung von f in (x°,f(x°)), jetzt im R^m.

Totales Differential von f(x1,x2,...):
Das Prinzip wird an einer Abb.im R³ gezeigt:
Abb: {(x1,x2,z) F=(z-f(x1,x2))=0 }. Die Quell-Menge ist die Ebene mit 2-Basis-Richtungen in Richtung der Variablen x1,x2.
Gegeben seien 3 Punkte, p0,p1,p2. Differentiale sind Differenzen zwischen beliebigen Punkten, z.B. (p1-p0)=Δp1 oder (p2-p0)=Δp2.
Liegen die Differentiale in Richtung der Koord. {x1,x2}, werden sie symb.: Δx1 /Δx2 bezeichnet. Die Diff. (p1-p0) u.(p2-p0) in Koord.Schreibweise:
(p1-p0)= (x₁₁, x₁₂)- (x₀₁, x₀₂)
(p2-p0)= (x₂₁, x₂₂)- (x₀₁, x₀₂)
Liegen (p1-p0),(p2-p0) in Richtung x1,x2, dann sind die 2.Koord.gleich:
(p1-p0)= (x₁₁-x₀₁, x₀₂-x₀₂)
(p2-p0)= (x₀₁-x₀₁, x₂₂-x₀₂)
=> (p1-p0)= (x₁₁-x₀₁ , 0)= Δ₁x ,=> x₁₁= x₀₁+ Δ₁x
=> (p2-p0)= (0 , x₂₂-x₀₂)= Δ₂x ,=> x₂₂= x₀₂+ Δ₂x
(Δ₁x, Δ₂x sollen hier an p0 gedockt sein.)
Mit den Bildpunkten f(p0),f(p1),f(p2) können die korrespondierenden Bild-Differentiale Δ₁f, Δ₂f gebildet werden:
f(p1)-f(p0)= > f(x₀₁+Δ₁x , x₀₂)- f(x₀₁ , x₀₂) = Δ₁f
f(p2)-f(p0)= f(x₀₁ , x₀₂+Δ₂x)- f(x₀₁ , x₀₂) = Δ₂f
Δ₁f, Δ₂f sind die part.Bild.Diff. für die entspr. Quell-Richtungen (hier x1,x2).
Das Gesamt- oder totale Bild-Diff. Δf(Δ₁x+Δ₂x ) wäre dann:
Δf= f(x₀₁+Δ₁x , x₀₂+Δ₂x)- f(x₀₁ , x₀₂)     Erweitern:
  = [f(x₀₁+Δ₁x , x₀₂+Δ₂x) - f(x₀₁ , x₀₂+Δ₂x) ] *Δ₁x/Δ₁x
    +[f(x₀₁ , x₀₂+Δ₂x) - f(x₀₁ , x₀₂) ] *Δ₂x/Δ₂x
=>  Δf= D₁f*Δ₁x + D₂f*Δ₂x    totales Differential von f

Menge {f} der stetig diff.baren Funktionen:
Δf/Δx= Df   Grundform der Beziehung zwischen Diff.Quotienten u.Ableitung f
Δf= Df*Δx   direkte Relation zwischen Bild-und Quell-Differential. Der Relationsfaktor ist die Ableitung von f am Quellpkt. "x", an dem auch die Differentiale angedockt sind.
Die Ableit.höherer Ordnung werden iterativ def.:
g=Df,   Δg= Dg*Δx   in linken Term: "g" -> "f" ersetzen:
ΔΔf= Dg*Δx   in rechtem Term: "Dg" -> "Df*Δx" ersetzen:
ΔΔf= DDf *Δx*Δx   Symb.: ΔΔ = Δ² , Δx*Δx = (Δx)² setzen:
Die Abl. einer Funktion g=Df ist 2.Ableitung der Funktion f:
Symb.: Δ²f = D²f *dx²

Abl. von f=f(x,y):
g= D(f(x,y))  Δg als totales Diff. schreiben:
Δg= D₁g*Δ₁x + D₂g*Δ₂x   "g" in rechtem Term durch totales Diff.  Δf ersetzen:
   = D₁[ D₁f*Δ₁x + D₂f*Δ₂x] *Δ₁x
     +D₂[ D₁f*Δ₁x + D₂f*Δ₂x] *Δ₂x   Glieder entspr. "Binom" zusammenfassen:
Δg= D₁²f*Δ₁x²   +2*D₁D₂f*Δ₁x*Δ₂x   +D₂²f*Δ₂x²
Satz von 'Schwarz':
Wegen der Verknüpfungen über Lin.-Komb. kann die Reihenfolge der part.Abl. vertauscht werden:
D_kD_jf = D_jD_kf   Die Indexfolge bei mehrfach part.Abl. kann innerhalb vertauscht werden!

Potenzreihen-Entw. für f(x,y):
Sei (x,y)=(x1,x2), p0=(x1°,x2°), Δ_jx = (xj-xj°) ,j=1,2
Dann gilt für die   a(j)*(x-x°)^j= 1/j!*D^jf₀*(x-x°)^j .
Im rechtem Term:
D^jf₀= ersetzen durch totales Diff. j-ter Ordnung
(x-x°)^j= ersetzen durch Binom j-ter Ordnung
(j)-te Summanden:
(0)= 1/0!*D⁰f(x°)*(x-x°)⁰= 1
(1)= 1/1!*[ D₁f(x°)*(x1-x1°) + D₂f(x°)*(x2-x2°)]
(2)= 1/2!*[ D₁²f(x°)*(x1-x1°)²
        + 2D₁D₂f(x°)*(x1-x1°)(x2-x2°)
         + D₂²f(x°)*(x2-x2°)² ]
(3)= 1/3!*[ D₁³f(x°)*(x1-x1°)³
        + 3D₁²D₂f(x°)*(x1-x1°)²(x2-x2°)
        + 3D₁D₂²f(x°)*(x1-x1°)(x2-x2°)²
         + D₂³f(x°)*(x2-x2°)³ ]
(4) ...(n-1). Dies ist die Taylor-Form der Potenzreihe für f.
Im Restglied im (n)-Koeff. ist f(x=x~) ein Punkt, welcher auf der Verb.Linie zwischen x und x° liegt.
Def:  Die durch die Koeff. (0)...(n-1) zuvor definierte Potenzreihe heißt: Näherungspolynom (n-1)-ter Ordnung P_n-1() für f zum Punkt x°.
Abschätzung der part.Abl.Komb. 3-ter Ordnung:
Abs(D_v1D_v2D_v3) ≤K_v1v2v3 , v(i)=1 oder 2
Beispiel: f=x1⁴x2x1, D₁³f=24x1, D₂D₁²f=0 , D₂²D₁f=0 , D₂³f=0, für {x, 0≤x≤2} gilt:   K₁₁₁=Abs(D₁³f)≤24*2 , K₂₁₁=K₂₂₁=K₂₂₂=0 .
Polynom umstellen:
f= P_n-1() +R(n)   Rechte Seite erweitern:
f= P_n-1() +a(n)*(x-x°)ⁿ +[ R(n) - a(n)*(x-x°)ⁿ] =>
f= P_n() +[ R(n) - a(n)*(x-x°)ⁿ] Term in [] wird folgend abgeschätzt:
Abschätzung  f-P_n():
v₁....v_n sei die Indexfolge der n-part.Abl. von f.
ε>0 vorgegeben, => ∃δ_ε>0, so das gilt:
Abs(D_v1....vnf - D_v1....vnf(x°) ) <ε , ∀x∈Uδ_ε(x°)
Daraus folgt für (f-P_n) :
Abs(f-P_n)< 1/n! *ε[ Sum( Abs(x_v1-x_v1°) *....*Abs(x_vn-x_vn°) ]

Beispiel:
Es sei zu f=x1+x2³, x'=(0,0) und x"=(1,2) der Pkt. x~ des Restgliedes zu bestimmen:
D₁f=1, D₂f=3x2², D₁²f= D₁D₂f= D₂D₁f=0, D₂²f=6x2
Verb.Strecke von p1-p2: x(t)=(t,2t), 0≤t≤1 .
Entwickl. f=P₁() +R(2) zwischen Pkt. x",x':
f(x")= f(x') +1/1!*[D₁f(x')*(x1"-x1') +D₂f(x')*(x2"-x2')]
        + 1/2!* [ D₁²f(x~) *(x1"-x1')² ]
        + 1/2!* [2D₁D₂f(x~)*(x1"-x1')(x2"-x2') ]
        + 1/2!* [ D₂²f(x~) *(x2"-x2')² ]
x~(t~)=(t~,2t~), da alle 2.Abl.Null sind, bis auf D₂²f(x~)=6*2*t~ , ergibt die Gesamt-Entw.:
f(x")= 1+2³=9, f(x')=0, x"-x'=(1-0,2-0), D₂²f(x~) *(x2"-x2')²= 12(t~)*2² , Werte einsetzen:
9= 0 +1+0 +0+(0+0) +1/2!*12(t~)*4   Gl. nach t~ auflösen:
8= 24*t~, t~=1/3, x~=(t~,2t~)= (1/3, 2/3).
Bemerkung:   In diesem Fall gibt es nur einen einzigen Pkt.x~, i.a. mehrere!

Beispiel:
f=x₁⁴+x1x2 .Es ist zum Pkt.x°=(1,1) das Näherungspolynom 2.Ordnung zu bestimmen:
D₁f=4x₁³+x2, D₂f=x1, D₁²f=12x₁², D₁D₂f=1, D₂²f=0, also:
f(x°)=2, D₁f(x°)=5, D₂f(x°)=1, D₁²f(x°)=12, D₁D₂f(x°)=1, D₂²f(x°)=0, Polynom(2):
Nachfolgend wird x1° durch 1 und x2° durch 1 ersetzt!
P₂(x)= P_n(x1,x2)= 2 +
      +1/1!*[5(x1-1) +1(x2-1)]
      +1/2!*[ 12(x1-1)² +2*1(x1-1)(x2-1) +0*(x2-1)² ]
   = 2 +5(x1-1) +(x2-1) +6(x1-1)² +2(x1-1)(x2-1)
Abschätzung mit 3.Abl.:
D₁³f=24x1, D₁D₂²f= D₁²D₂f= D₂³f=0
Für M={(x1,x2): 0≤x1≤2 , (x2 hier egal) } gilt:
Abs(D₁³f)≤ 24*2= 48= K₁₁₁ , K₂₁₁=0 ... usw.
Abs(f(-P₂)≤ 1/3!*[K₁₁₁(x1-1)³ +0...]=8(x1-1)³
Die Abschätzung hängt hier nur von x1 ab. Ist z.B. Abs(x1-x1°)=Abs(x1-1) <1/10 , so ist:
Abs(f(-P₂)< 8/10³ .
Ende Beispiele

Voraussetzungen:
M°= offenes Intervall im R^m   , z.B.  a≤x≤b
f∈C⁽¹⁾(M°)   , Menge aller in M° setig-diff.barer Funktionen
M⊂M°   , M= kompaktes Intervall in M°
x°∈M   , Punkt im kompakten Intervall, a<x<b
dann gilt:
Das Näherungspolynom P₁(x)= f(x°) +Df(x°)(x-x°) heißt "Linearisierung" von f in x° .
Erläuterung:
P₁() ist eine lineare Funktion über der Quell-Menge M, also eine Abbildung im R^m+1:
{(x,z): z= f(x°) +Df(x°)(x-x°) ,x∈R^m, z∈R¹ }
Der Graph der Linearisierung heißt im:
R¹⁺¹:   "Tangente" an f im Pkt. (x°,f(x°)) .
R²⁺¹:   "Tangential-Ebene" an f in(x°,f(x°) :
    {(x1,x2,z):  z= f(x°) +D₁f(x°)(x1-x1°) +D₂f(x°)(x2-x2°) }
R³⁺¹:   "Hyper-Ebene" an f   im R^(m+1)-1.

Beispiel R¹⁺¹:
Entsprechend Überlegungen aus vorigem Kapitel kann f-P₁ auf 2 Arten abgeschätzt werden:
1.   Abschätzung mit 2.Ableitung:
    Abs(f-P₁)≤ 1/2!*Abs[D²f(x~))*(x-x°)],
    x∈U_δ(x°)= {x: Abs(x-x°)≤a } ,x~ durch x° ersetzen:
    Abs(f-P₁)≤ 1/2!*Abs(D²f(x°))*a²
2.   Abschätzung in Linearisierung selbst:
f(x)= f(x°) +Df(x~)(x-x°) ,entspricht Mittelwertsatz
Rechte Seite erweitern:
f= f(x°) +Df(x°)(x-x°) +[Df(x~)) -Df(x°)] (x-x°)
Da Df stetig ist, wird der unterstrichene Term <ε bei x∈U_δ(ε)(x°).
Also gilt:   Abs(f-P₁)≤ ε*Abs(x-x°)

Anwendung Fehlerrechnung:
Wir betrachten eine Funktion y=f(x1,x2) in der Umgebung von x°=(x1°,x2°).
Ist x° nur ungefähr bestimmt, z.B. bei Messungen, so gilt für x_j:
x_j°-Δx_j ≤ x_j°+Δx_j , weiter sei f(x)-f(x°)= Δy
Wird f in Δy durch P₁ ersetzt, erhält man für Δy einen ungefähren Wert Δy~ :
Δy~ = P₁(x) -f(x°)= Df(x°)(x-x°)   , 1-dim
      = D₁f(x°)(x1-x1°) +D₂f(x°)(x2-x2°)   ,2-dim
      = D₁f(x°)Δx₁ +D₂f(x°)Δx₂ + ...   ,m-dim
Beispiel Erdbeschleunigung:
Die Erdbeschleunigung g steht für die Wechselwirkung zwischen Fallzeit t und Fallhöhe s, ist als eine Funktion y= f(s,t)= 2s/t² .
Gemessene Werte seien x°=(s°,t°), die Messfehler Δs, Δt. Es gilt:
y°= f(s°,t°)= 2s°/t°² ,D_sf(x°)= 2/t°² ,D_tf(x°)= -4*s°/t°³ , also:
Δy~ = 2/t°²Δs - 4*s°/t°³Δt   =>
Abs(Δy~)≤ 2/t°²Δs +4*s°/t°³Δt , Δy~/y° = "Relativer Fehler, =>
Abs(Δy~/y°)≤ [ 2/t°²Δs + 4*s°/t°³Δt ] *2s°/t°²   =>
Abs(Δy~/y°)≤ Δs/s° +2*Δt/t°
( Δs/s° ,Δt/t° =relative Fehler von s bzw. t)

Linearisierung komplexer Funktionen:
f= (f1,f2)= f1 +i*f2 , f1,f2 ∈C⁽¹⁾(M)
Als Quell-Mengen kommen:
1.  M= kompaktes Intervall auf t-Achse (R¹),
2.  M= offene Menge in (kompl.) z-Ebene.
Linearisierung zu 1. :
Linearisierung f1~,f2~ von f1,f2 im Pkt. t° :
(1)   f_j~(t)= f_j(t°) +Df_j(t°)(t-t°) , j=1,2
f~(t)= f₁(t°)+if₂(t°) +[ Df₁(t°)+iDf₂(t°) ](t-t°)   Koord.Form
Def:   Df(t°)= Df₁(t°)+iDf₂(t°) heißt: Differentialquotient der kompl.Funktion f bezügl. der reellen Variablen t im Pkt. t°.
Denn: Gl.(1) rückwärts Δf_j/(t-t°) , j=1,2:
Lim((t°->t)f_j~(t)- f_j(t°)]/(t-t°) =Df_j(t) , j=1,2
Linearisierung f~ von f im Pkt. t° :
(1)   f~(t)= f(t°) +Df(t°)(t-t°)   kompl. Form
Beispiel:
M= {t: 0≤t≤1}, f(t)= t² +it³, Df(t)= 2t +3it².
Satz 1:   Besitzen f,g in t° Diff.Quotienten Df,Dg, so gilt dasselbe auch für:
D(f±g) = Df ± Dg
D(f*g) = Df*g +f*Dg
D(f/g) = (Df*g -f*Dg)/g²

Beispiel:
Linearisierung in kompl.Form für "1 zu 1" -Abbildung der Ebene:
M= {t: f(z)=z, z= r*exp(it), r=Param. fest}   Graph ist Kreislinie(r) Bildauswertung:
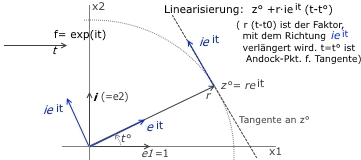
{exp(it), i*exp(it)} sind neue (karth.) Basis-Koord. der Ebene, (Siehe Kap. 6.7 Rechnen mit komplexen Zahlen, Absatz: 'Koord. in Richtung z').
Bei kompl.Funktionen einer reellen Variablen, in geometr. Assoziierung mit Newton-Raum, geben sie die Kurven-/Linien-Richtung an, z.B. bei Bewegungen von Körpern: Bahn-Geschw., -Beschl., Zentrifugal/-pedal-Kräfte etc.

Achtung: In diesem Kapitel wird mit * nach der kompl.Zahl, die zugehörige konj.kompl.Zahl gekennzeichnet!
Das normale "*" kennzeichnet im Produkt das Mult.Zeichen.
Das hochgestellte °-Zeichen, soll einen festen Punkt/Zahl p₀ kennzeichnen.

Im vorigen Kap.6.10 wurden kompl.Funktionen einer reellen Variablen durch lineare Funktionen (P₁)(t)) approximiert. Jetzt ist die Quellmenge ein abgeschlossener Bereich in der Ebene:
z=x1+i*x2, f=(f1,f2)= f1(z) +i*f2(z), f1,f2∈C⁽¹⁾(M°).
Bemerkung:   f ist eine Abb. im R²⁺², der Graph der Abb. eine allg. 2-dim Menge im Abb.Raum.
Es sei z°∈M°, z°= x₀₁ +i*x₀₁ fest gewählt. Die Linearisierungen f1~,f2~ von f1,f2 im Punkt z° lauten:
f_j~(z)= f_j(z°) +D₁f_j(z°)(x1-x₀₁) +D₂f_j(z°)(x2-x₀₂) , j=1,2
Die Diff.Quotienten sind hier part.Diff.Quotienten nach x1° bzw. x2°, zusammengefaßt als "z°" bezeichnet. Damit ergibt sich für die Linearisierung f~ von f:
f~(z)= f1~(z) +if2~(z)=
          f₁(z°) +D₁f₁(z°)(x1-x₀₁) +D₂f₁(z°)(x2-x₀₂)
   +i*[ f₂(z°) +D₁f₂(z°)(x1-x₀₁) +D₂f₂(z°)(x2-x₀₂) ]
Nach Summanden zusammenfassen:
f~(z)=   f₁(z°) +i* f₂(z°)
   + [ D₁f₁(z°) +i*D₁f₂(z°) ]*(x1-x₀₁)
   + [ D₂f₁(z°) +i*D₂f₂(z°) ]*(x2-x₀₂)
Def:   Die unterstrichenen Ausdrücke zuvor heißen: part.Diff.Quotienten von f nach x1,x2:
D₁f(z°)= D₁f₁(z°) +i*D₁f₂(z°)
D₂f(z°)= D₂f₁(z°) +i*D₂f₂(z°)
f~(z) umstellen:
Die Linearisierung im Pkt.z° ergibt sich dann zu:
f~(z)= f(z°) +D₁f(z°)(x1-x₀₁) +D₂f(z°)(x2-x₀₂)
Um aus (x1-x₀₁) u. (x2-x₀₂) "z-z°" zu machen: z-z°= (x1-x₀₁) +i(x2-x₀₂) , wird Folgerung2 aus Kap.6.7 "Rechnen mit kompl.Zahlen" wie folgt angewandt:
x1-x₀₁= 1/2[(z-z°)+(z-z°)*]= 1/2(z-z°) +1/2(z-z°)*
x2-x₀₂= 1/2i[(z-z°)-(z-z°)*]= -i/2(z-z°) +i/2(z-z°)*
f~(z) jetzt schreiben:
f~(z)=   f(z°)
     + 1/2*( D₁f(z°) -iD₂f(z°) )(z-z°)
     + 1/2*( D₁f(z°) +iD₂f(z°) )(z-z°)*
Die Koeff. vor der kompl.Zahl (z-z°) bzw. vor der konj. kompl.Zahl (z-z°)* heißen "part. kompl. Diff.Quotienten" der kompl.Funktion f bezuüglich "z" bzw. "z*".
Symb.:   D_zf(z°) , D_z*f(z°)
(1)   D_zf= 1/2*( D₁f - iD₂f)
(1a)  D_z*f= 1/2*( D₁f + iD₂f)
Die Linearisierung lautet jetzt wie folgt:
f~(z)=   f(z°) +D_zf(z°)(z-z°) +D_z*f(z°)(z-z°)*  oder:
(2)  f~(z) -f(z°)= D_zf(z°)(z-z°) +D_z*f(z°)(z-z°)*

Graph der Linearisierung:
R²⁺²: {(z,z*,w): w=f~(z,z*) } , w ist (2-dim) kompl. Bildraum.
Erläuterung:
Der Graph ist eine Hyper-Ebene im R⁴, die eine Lin.Komb. aus Bild der z-Ebene und Bild der z*-Ebene darstellt. D.h. eigentlich 4-Quell-Variablen, die paarweise zusammenhängen: (x1,x2,x1,-x2).
Um eine Übereinstimmung mit der reellen, 2-Dim-Taylorreihe,P₁(x1,x2), zu bekommen, fordert man entweder D_z*f(z°)=0 oder D_zf(z°)=0. Dann kann man einen vergleichbaren "Mittelwertsatz" kompl. Abbild. wie folgt formulieren.

Mittelwertsatz kompl. Abbild.:
Existiert zu einer kompl. Abbildung f der Diff.Quotient D_zf(z°) im Pkt.z°, dann gilt Gl.(2):
f(z) -f(z°)= D_zf(z°)(z-z°) +0 ,wenn D_z*f(z°)=0 ist.
oder: [f(z) -f(z°)]/(z-z°) =D_zf(z°) , für ein z aus U_δ(z°)
Satz1:   Existiert Lim [f(z)-f(z°)]/(z-z°) , ∀z° ∈M , dann ist f holomorph (siehe Unten) und es gilt:
D_zf(z)= Lim [f(z)-f(z°)]/(z-z°) , z<->z°

Satz 2:   Besitzen f,g in z° den "part.kompl. Diff. Quotienten" D_z() , D_z*(), so gilt dasselbe auch für:
D(f±g) = Df ± Dg
D(f*g) = Df*g +f*Dg
D(f/g) = (Df*g -f*Dg)/g²   äquivalent zu Satz1 aus 6.10 "Linearisierung von f(t) in t°"

Beispiele:
a)  f=const., so ist D₁f(z)= D₂f(z)= 0 und D_zf= D_z*f= 0
b)  f= z= x1+ix2, D₁f(z)=1, D₂f(z)= i
      D_z(z)= 1/2( 1 -i²)= 1,
      D_z*f= 1/2( 1 +i²)= 0   Wichtige Aussage!
c)  f= z*= x1-ix2, D₁f(z)=1, D₂f(z)=  -i
      D_z(z*)= 1/2( 1 -i(-i))= 0,  Wichtige Aussage!
      D_z*f= 1/2( 1 +1)= 1
d)  D_z(zⁿ)= n*D_z(z^n-1) , D_z*(z*)ⁿ= n*D_z*(z*)^n-1
      (Beweis durch vollst. Induktion aus Satz1 und b) und c))
e)  c₀,c₁,...,c_k kompl. Konst., dann gilt für:
      f(z,z*)= c₀z₀ +c₁z + ...+ c^kz^k :
      D_zf= 0 +(1*c₁)z₀ +(2c₂)z + ...+ (k*c^k)z^k-1
      D_z*f= 0 +0 +0 +...+0
f)  Analog zu e) für Diff. z*:
      f(z,z*)= c₀z*₀ +c₁z* + ...+ c^k(z*)^k :
      D_zf= 0 +0 +0 +...+0
      D_z*f= 0 +(1*c₁)z*₀ +(2c₂)z* + ...+ (k*c^k)z*^(k-1)
Beispiele e) und f) sind Basis für Potenz. Entw. kompl. Funktionen ! Siehe dazu auch Bemerkung zu Satz1

Def:   Wenn die part. kompl. Diff. Quotienten D_zf und D_z*f überall im Quellgebiet M existieren, dann heißt:
f holomorph , wenn D_z*f(z,z*)= 0 , ∀z ∈M
f antiholomorph , wenn D_zf(z,z*)=D_zf(z,z*)= 0

Satz3:   wegen Gl.(1),(1a) gilt für f:
f holomorph, dann: -i*D₂f= D₁f , =>  D_zf= D₁f = -i*D₂f
f antiholom., dann:   i*D₂f= D₁f , =>  D_z*f= D₁f = i*D₂f
oder (part.Abl.):
f holom. : D₁f₁= D₂f₂ , D₁f₂= -D₂f₁
f antihol.: D₁f₁= -D₂f₂ , D₁f₂= D₂f₁
(Die Vorzeichen sind diagonal vertauscht! )

Differentiale in den verschied.Ebenen:
Wir gehen von der allg. Abbildung R² ->R² aus:
f= f1+i*f2= f1(x1+i*x2) +i*f2(x1+i*x2)
Die Differentiale der Quell-Ebene sind: Δx1, Δx2 und der Bild-Ebene: Δf1, Δf2.  Alle Diff. sind an dem allg.Pkt. z°=(x1°,x2°), f(z°) angedockt.
Handelt es sich bei f1,f2 um stetig diff.bare Funktionen, so besitzen alle part. Diff. Quotienten Grenzwerte im allg.Pkt. z°:
(1) D₁f₁= Δf1/Δx1 , D₁f₂= Δf2/Δx1
(2) D₂f₁= Δf1/Δx2 , D₂f₂= Δf2/Δx2
Die 4 Diff.Quotienten sind reelle Zahlen und können in einer weiteren Ebene als 2 kompl. Zahlen dargestellt werden (D₁f₁ +i*D₁f₂) und (D₂f₁ +i*D₂f₂) .

1. kompl.Funktion einer Variablen:
Quelle: {x1=t, x2=0} f(t)= f1(t)+ i*f2(t) , 2 part.Abl.: Df1, Df2 Bildauswertung:
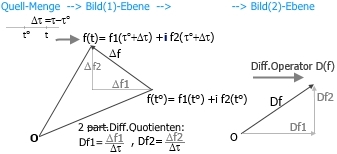
Δf₁= f₁(t°+Δt)-f₁(t°) , Δf₂= f₂(t°+Δt)-f₂(t°)
Die Diff.Quotienten sind reelle Zahlen, d.h., der Differential-Operator D() ist selbst eine ganz normale Abbild. in die Ebene (->Bild(2)).

2. kompl.Funktion zweier Variablen:
{(x₁,x₂):   f= [f1(x₁,x₂),f2(x₁,x₂)] }
f1,f2 sind reelle Funktionen einer kompl.Variablen. f ist kompl. Re[f]= f1 ,Im[f]= f2
f kann holomorph, antiholomorph oder keines von Beiden sein.
Im nachf. Bild wird die Abb. des Diff.Operators D() einer kompl.Funktion f untersucht: Bildauswertung:
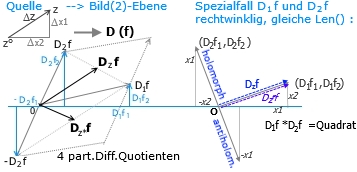
Die part.kompl.Diff.Quotienten (1) und (2) bilden Richtungen (D₁f ,D₂f) in der Ebene, die im Spezialfall der "holomorphie" bzw. "antiholom." von f im Rechten Winkel zueinander stehen, und die gleichen Längen haben.
Dann gilt:  D_zf bzw. D_z*f = D₁f₁ +i*D₁f₂
(Wegen Satz3 aus Kap.6.11 zuvor)
Beweis:
Wir bezeichnen die D₁-Richtung mit X₁ und
die D₂-Richtung mit X₂. Dann gilt:
f holom. : x_1,1=x_2,2 , x_1,2=-x_2,1   =>
      X₁= (x_1,1,x_1,2) , X₂= (-x_1,2,x_1,1)
f antihol.: x_1,1=-x_2,2 , x_1,2=x_2,1   =>
      X₁= (x_1,1,x_1,2) , X₂= (x_1,2,-x_1,1)
(Die Vorzeichen ändern sich in X2)
d²(X₁)= d²(X₂)= x₁₁² +x₁₂²
Flächenprodukt F(X₁,X₂)= ±(x₁₁² +x₁₂²)
F(X)/d²(X)= ±d²(X)/d²(X)= ±1   = rechtwinklig, gl.Len,
Das neg-Vz. ergibt sich bei antiholom. f
Skapro(X1,X2)= x₁₁*x₁₂ - x₁₁*x₁₂= 0
Ende des Beweises