| 2. Einfache geometr.Objekte der Euklidischen Geometrie zurück |
Ausgangspunkt
Die Eukl.Geometrie hat sich von Anbeginn der Menschheit entwickelt, ohne die
erst später dazugekommenen math.Wissenschaften, wie Analysis, Analytische Geometrie,
Newtonsche Mechanik usw. zu verwenden und ohne die neuen Computer-Berechnungs-Methoden
mit einzubeziehen.
Die Eukl.Geometrie ist eine konstruktive Geometrie (mit Zirkel und Lineal) und verwendet für ihre untersuchten Objekte im Wesentlichen nur die Operationen/ Transformationen:
- Verschieben
- Drehen
- Umklappen/Spiegeln
- Zoomen/Ähnl.Transformation
- Relationen(Beziehungen) zwischen ration.Zahlen
- elementare math.Verknüpfungen
Werkzeuge für die Transformationen sind: Zirkel, Lineal, rechtw.Dreieck und Winkelmesser (mit 1/2 Kreisbogen u. 180°-Teilung). Mit diesen Werkzeugen lassen sich alle nachf. beschriebenen Kontruktionen ausführen.
Als elementare math.Verknüpfungen werden nur Add/Sub , Mult/Div sowie Mult. gleicher Zahlen =Potenz verwendet.
Zu den verwendeten Zahlen ist zu sagen:
Man ging für die Bemaßung von elemtaren geometr.Objekte (Längen, Flächen, Winkeln etc ) von zunächst ganzen Zahlen aus, und kam durch Teilungs-Operationen schnell auf rationale Zahlen p/q; p,q ganze Zahlen: 1,2,3,.... .
In der Folge stellte man aber fest, dass z.B. bestimmte Relationen: Fläche-Rechteck zu Länge-Diagonale oder Länge-Kreisbogen zu Kreis-Durchmesser keine ration.Zahlen mehr ergeben! Genaueres wird in der Analyt.Geometrie untersucht.
Die Methoden der Eukl.Geometrie-(Ebene) basieren auf folgenden (kontruktiven) Axiomen:
1.Axiom: 2 Geraden schneiden sich in einem Punkt, wenn sie nicht parallel sind.
2.Axiom: Zwischen 2 Punkten auf einer Geraden ensteht eine Strecke. Ist die Länge der Strecke=NULL, dann sind die beiden Punkte identisch.
3.Axiom: Das Verhältnis zwischen Länge-Vollkreislinie und dessen Durchmesser d, d>0, ist konstant. Diese Konstante heißt "pi"
Das 3.Axiom verwundert hier ein wenig, ist aber in sofern gültig, als dass es bisher noch keinem Menschen gelungen ist, einen Kreis zu konstruieren, bei dem besagtes Verhältnis ungleich pi ist!
Bemerkung1: Konstruktiv kann man den Wert von pi nur auf wenige Nach-Komma-Stellen bestimmen. Neuere Computer-Programme können pi bis auf beliebige n-Stellen nach dem Komma berechnen, n natürliche Zahl (kleiner unendlich).
Bemerkung2: In vielen Publikationen wird das sogenannte Parallel-Axiom zur Axiomatik hinzugenommen. Da wir hier aber einen konsequent kontruktiven Ansatz verfolgen, ergibt sich die Eigenschaft "parallelität" aus den verwendeten Kontruktions-Prinzipien!
Bemerkung3: Die (kontruktive) Beweisführung zu den festgestellten Aussagen in der Eukl.Geometrie basieren immer auf der gesicherten Annahme, daß es bisher noch keinem Menschen gelungen ist, entspr. Gegenbeispiele zu konstruieren!
Beginnen wollen wir mit dem einfachsten 2-dim geometr.Objekt in der Ebene, dem Dreieck, siehe folgend!
Die Eukl.Geometrie ist eine konstruktive Geometrie (mit Zirkel und Lineal) und verwendet für ihre untersuchten Objekte im Wesentlichen nur die Operationen/ Transformationen:
- Verschieben
- Drehen
- Umklappen/Spiegeln
- Zoomen/Ähnl.Transformation
- Relationen(Beziehungen) zwischen ration.Zahlen
- elementare math.Verknüpfungen
Werkzeuge für die Transformationen sind: Zirkel, Lineal, rechtw.Dreieck und Winkelmesser (mit 1/2 Kreisbogen u. 180°-Teilung). Mit diesen Werkzeugen lassen sich alle nachf. beschriebenen Kontruktionen ausführen.
Als elementare math.Verknüpfungen werden nur Add/Sub , Mult/Div sowie Mult. gleicher Zahlen =Potenz verwendet.
Zu den verwendeten Zahlen ist zu sagen:
Man ging für die Bemaßung von elemtaren geometr.Objekte (Längen, Flächen, Winkeln etc ) von zunächst ganzen Zahlen aus, und kam durch Teilungs-Operationen schnell auf rationale Zahlen p/q; p,q ganze Zahlen: 1,2,3,.... .
In der Folge stellte man aber fest, dass z.B. bestimmte Relationen: Fläche-Rechteck zu Länge-Diagonale oder Länge-Kreisbogen zu Kreis-Durchmesser keine ration.Zahlen mehr ergeben! Genaueres wird in der Analyt.Geometrie untersucht.
Die Methoden der Eukl.Geometrie-(Ebene) basieren auf folgenden (kontruktiven) Axiomen:
1.Axiom: 2 Geraden schneiden sich in einem Punkt, wenn sie nicht parallel sind.
2.Axiom: Zwischen 2 Punkten auf einer Geraden ensteht eine Strecke. Ist die Länge der Strecke=NULL, dann sind die beiden Punkte identisch.
3.Axiom: Das Verhältnis zwischen Länge-Vollkreislinie und dessen Durchmesser d, d>0, ist konstant. Diese Konstante heißt "pi"
Das 3.Axiom verwundert hier ein wenig, ist aber in sofern gültig, als dass es bisher noch keinem Menschen gelungen ist, einen Kreis zu konstruieren, bei dem besagtes Verhältnis ungleich pi ist!
Bemerkung1: Konstruktiv kann man den Wert von pi nur auf wenige Nach-Komma-Stellen bestimmen. Neuere Computer-Programme können pi bis auf beliebige n-Stellen nach dem Komma berechnen, n natürliche Zahl (kleiner unendlich).
Bemerkung2: In vielen Publikationen wird das sogenannte Parallel-Axiom zur Axiomatik hinzugenommen. Da wir hier aber einen konsequent kontruktiven Ansatz verfolgen, ergibt sich die Eigenschaft "parallelität" aus den verwendeten Kontruktions-Prinzipien!
Bemerkung3: Die (kontruktive) Beweisführung zu den festgestellten Aussagen in der Eukl.Geometrie basieren immer auf der gesicherten Annahme, daß es bisher noch keinem Menschen gelungen ist, entspr. Gegenbeispiele zu konstruieren!
Beginnen wollen wir mit dem einfachsten 2-dim geometr.Objekt in der Ebene, dem Dreieck, siehe folgend!
Diese Abhandlung besteht aus folgenden Abschnitten:
1.0
Dreieck
->1.0
1.1.
Kreise, Winkel und Winkel im Dreieck
->1.1
1.2.
Def. von Punkt und Gerade
->1.2
1.3.
Senkrechte, Mittel-Senkrechte, Lot
->1.3
1.4.
Verschieben, Drehen, Spiegeln, Zoomen
->1.4
1.5.
Parallelität von Geraden
->1.5
1.6.
Triangulation der Ebene (Überdeckung mit verschied. Rastern )
->1.6
1.7.
Messen und Vergleichen von Strecken
->1.7
1.8.
Kreise und Dreiecke (Außen-/Innenkreis und Tangente /Sekante u. Pythagoras)
->1.8
1.9.
Zerlegung des Dreiecks in 2 rechtw.Dreiecke
->1.9
1.10.
Winkelsummen im Dreieck
->1.10
1.11.
Fläche der Kreisscheibe (Grenzübergange ->∞ ,Definition Tangente)
->1.11
1.12.
Allg. geometr. Objekte (δ-Umgeb. , offene-/kompakte Intervalle )
->1.12
1.13.
Teilung der Eins-Strecke und Rat.Zahlen (Abzählbare Mengen, Potenzreihen)
->1.13
1.14.
Rationale Zahlen als Repräsentant von Potenzreihen und umgekehrt
->1.14
1.15.
Zusammenfassung
->1.15
1.0 Dreieck
3 Geraden schneiden sich in der Ebene, wenn sie nicht paarweise parallel sind
(entspr. Axiom1).
Bild , Eukl-geo1.jpg

Satz:
1.Teil: Aus 3 vorgegeben Strecken a, b, c lassen sich genau 2 eindeutige Dreiecke konstruieren, die sich nur in der Reihenfolge ihrer Strecken unterscheiden, aber betragsmäßig die gleiche Fläche haben:
1. eindeut.Dreieck D : (a,b,c)
2. eindeut.Dreieck D': (a,c,b)
Dies funktioniert nur unter der Voraussetzung, dass die längste der 3 Strecken kleiner ist, als die Summe der beiden Kürzeren, also c≤a+b, wenn c die längste Strecke ist!
Gegenbeispiel: Zu der Kombination a=7, b=2, c=3 kann man kein Dreieck konstruieren, denn die Ungleichung 7≤2+3 stimmt nicht!
2.Teil: Bei jedem existierenden Dreieck ist die längste der 3 Strecken kleiner, als die Summe der beiden Kürzeren! (Diese Aussage ist vom fert.Dreieck aus betrachtet trivial, steht hier aber als Gegen-Aussage zum 1.Teil )
Beweis des Satzes:
Die Beweisführung wird kontruktiv vorgenommen (mit Zirkel und Lineal). Gegeben 3 Strecken a, b, c ; a≤b≤c und c≤a+b . Folgende konstruk.-Schritte durchführen:
a) Um einen Pkt.A 2 Kreisbögen mit r=b und r=c schlagen
b) Dann auf Kreisbogen(r=c) einen Pkt.B festlegen und um diesen Pkt.B einen Kreisbogen mit r=a schlagen. Dieser schneidet Kreisbogen(r=b) in einem Pkt.C
Das Ganze funktioniert, weil aus Ungleichung c≤a+b folgt: a≥c-b ! Sollten 2 Strecken gleich sein, bekommt man ein gleichschenkliges Dreicken, sollten alle Strecken gleich sein, dann ein gleichsetiges Dreieck. Im Extremfall, c=a+b, erhält man ein entartetes Dreieck, nämlich 3 Punkte auf der längsten Strecke c.
Bild , Eukl-geo2.jpg
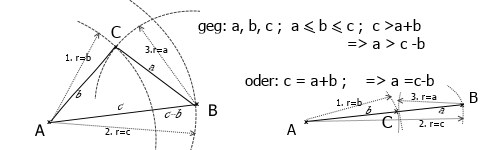
Da man 3 Punkte, die paarweise ungleich sind, immer paarweise mit Geraden verbinden kann, entstehen durch das Verbinden mit diesen Geraden 3 Strecken a, b, c zwischen den Punkten A, B, C ,von denen mind. 1 Strecke, z.B. c, die Längste ist.
Dann gilt, entspr. dem zuvor Gesagten, die Ungleichung c≤a+b auch für alle (positiven) Zahlen a,b,c ; c≥a , c≥b
Ende des Beweises
Diese Ungleichung wird wegen des Zusammenhanges zur Dreiecks-Konstruktion auch Dreiecks-Ungleichung genannt.
Qed.

Satz:
1.Teil: Aus 3 vorgegeben Strecken a, b, c lassen sich genau 2 eindeutige Dreiecke konstruieren, die sich nur in der Reihenfolge ihrer Strecken unterscheiden, aber betragsmäßig die gleiche Fläche haben:
1. eindeut.Dreieck D : (a,b,c)
2. eindeut.Dreieck D': (a,c,b)
Dies funktioniert nur unter der Voraussetzung, dass die längste der 3 Strecken kleiner ist, als die Summe der beiden Kürzeren, also c≤a+b, wenn c die längste Strecke ist!
Gegenbeispiel: Zu der Kombination a=7, b=2, c=3 kann man kein Dreieck konstruieren, denn die Ungleichung 7≤2+3 stimmt nicht!
2.Teil: Bei jedem existierenden Dreieck ist die längste der 3 Strecken kleiner, als die Summe der beiden Kürzeren! (Diese Aussage ist vom fert.Dreieck aus betrachtet trivial, steht hier aber als Gegen-Aussage zum 1.Teil )
Beweis des Satzes:
Die Beweisführung wird kontruktiv vorgenommen (mit Zirkel und Lineal). Gegeben 3 Strecken a, b, c ; a≤b≤c und c≤a+b . Folgende konstruk.-Schritte durchführen:
a) Um einen Pkt.A 2 Kreisbögen mit r=b und r=c schlagen
b) Dann auf Kreisbogen(r=c) einen Pkt.B festlegen und um diesen Pkt.B einen Kreisbogen mit r=a schlagen. Dieser schneidet Kreisbogen(r=b) in einem Pkt.C
Das Ganze funktioniert, weil aus Ungleichung c≤a+b folgt: a≥c-b ! Sollten 2 Strecken gleich sein, bekommt man ein gleichschenkliges Dreicken, sollten alle Strecken gleich sein, dann ein gleichsetiges Dreieck. Im Extremfall, c=a+b, erhält man ein entartetes Dreieck, nämlich 3 Punkte auf der längsten Strecke c.

Da man 3 Punkte, die paarweise ungleich sind, immer paarweise mit Geraden verbinden kann, entstehen durch das Verbinden mit diesen Geraden 3 Strecken a, b, c zwischen den Punkten A, B, C ,von denen mind. 1 Strecke, z.B. c, die Längste ist.
Dann gilt, entspr. dem zuvor Gesagten, die Ungleichung c≤a+b auch für alle (positiven) Zahlen a,b,c ; c≥a , c≥b
Diese Ungleichung wird wegen des Zusammenhanges zur Dreiecks-Konstruktion auch Dreiecks-Ungleichung genannt.
Qed.
Bemerkung zur Dreiecks-Ungleichung:
Bisher ist es noch keinem Menschen gelungen ein Dreieck festzulegen, bei dem
die Dreiecks-Ungleichung für die Seitenlängen nicht zutrifft. Deshalb
besitzt die Dreiecks-Ungleichung axiomatischen Charakter und man könnte
wie folgt formulieren:
Axiom 4: Sind A,B,C beliebige Punkte, und a,b,c die Strecken zwischen den Punkten, dann können a,b,c als Abstände zwischen den Punkten gedeutet werden und es gilt für diese Abstände die Dreiecks-Ungleichung in der Form:
abs(a) ≤ abs(b) + abs(c) ,abs()=absolut-Betrag
Die Dreiecks-Ungleichung wird in der Eukl.Geometrie aber nicht als eigenständiges Axiom geführt, weil sie nicht unabhängig ist und hier aus Axiom2 folgt.
Im n-dim Eukl.Raum Rn hat diese Ungleichung für Abstände von Punkten im Rn durchaus axiom.Charakter und wird dort als eigenständiges Axiom geführt!
Bemerkung zu D und D' aus Satz_zuvor:
Die beiden Flächen-gleichen Dreicke, die aus Vertauschung 2-er Seiten hervorgehen, können auch als Spiegelung/Umklappen von sich selbst betrachtet werden. Sie entstehen also aus eine der zulässigen Transformation (Umklappen =Spiegeln), siehe Abschnitt "1. Ausgangspunkt" dieser Abhandlung Eukl.Geometrie.
Sie sind immer Betrags-Flächen-gleich und i.a. nicht kongruent (Ausname gleich-schenklige Dreiecke). Symb. unterscheiden wir diese beiden Dreiecke durch: D= -D' oder -D=D'.
Demzufolge stehen die zugehörigen Flächen zu sich in der Beziehung: F(D')= -F(D) oder F(D)= -F(D')
Gesamtmenge der Dreickecke:
---- D ------- D'-----
(abc) (acb)
(bca) (bac)
(cab) (cba)
sie entstehen, spaltenweise, durch zykl. Vertauschung der Seiten, bzw. durch die Transformationen: Drehen und Verschieben.
Bemerkung zum entarteten Dreieck:
Gilt für 3 Seiten a,b,c: a<b<c und c>a+b , dann entstehen bei der oben beschriebenen Konstruktion mit Zirkel und Lineal 2 weitere Punkte C,D auf c=(A,B) und, wir haben es mit 4 Punkten, die auf einer Geraden liegen, zu tun. In der analytischen Geometrie geht man später den umgekehrten Weg und fragt: "Unter welcher Bedingung liegen 4 Pkte. auf einer Geraden (bei zuläss.Tranform.) ?".
Axiom 4: Sind A,B,C beliebige Punkte, und a,b,c die Strecken zwischen den Punkten, dann können a,b,c als Abstände zwischen den Punkten gedeutet werden und es gilt für diese Abstände die Dreiecks-Ungleichung in der Form:
abs(a) ≤ abs(b) + abs(c) ,
Die Dreiecks-Ungleichung wird in der Eukl.Geometrie aber nicht als eigenständiges Axiom geführt, weil sie nicht unabhängig ist und hier aus Axiom2 folgt.
Im n-dim Eukl.Raum Rn hat diese Ungleichung für Abstände von Punkten im Rn durchaus axiom.Charakter und wird dort als eigenständiges Axiom geführt!
Bemerkung zu D und D' aus Satz_zuvor:
Die beiden Flächen-gleichen Dreicke, die aus Vertauschung 2-er Seiten hervorgehen, können auch als Spiegelung/Umklappen von sich selbst betrachtet werden. Sie entstehen also aus eine der zulässigen Transformation (Umklappen =Spiegeln), siehe Abschnitt "1. Ausgangspunkt" dieser Abhandlung Eukl.Geometrie.
Sie sind immer Betrags-Flächen-gleich und i.a. nicht kongruent (Ausname gleich-schenklige Dreiecke). Symb. unterscheiden wir diese beiden Dreiecke durch: D= -D' oder -D=D'.
Demzufolge stehen die zugehörigen Flächen zu sich in der Beziehung: F(D')= -F(D) oder F(D)= -F(D')
Gesamtmenge der Dreickecke:
---- D ------- D'-----
(abc) (acb)
(bca) (bac)
(cab) (cba)
sie entstehen, spaltenweise, durch zykl. Vertauschung der Seiten, bzw. durch die Transformationen: Drehen und Verschieben.
Bemerkung zum entarteten Dreieck:
Gilt für 3 Seiten a,b,c: a<b<c und c>a+b , dann entstehen bei der oben beschriebenen Konstruktion mit Zirkel und Lineal 2 weitere Punkte C,D auf c=(A,B) und, wir haben es mit 4 Punkten, die auf einer Geraden liegen, zu tun. In der analytischen Geometrie geht man später den umgekehrten Weg und fragt: "Unter welcher Bedingung liegen 4 Pkte. auf einer Geraden (bei zuläss.Tranform.) ?".
1.1 Kreise, Winkel und Winkel im Dreieck
Nach Axiom3 kann man einen beliebigen Kreisbogen mit Radius=r um einen Pkt.A
auf 2 verschiede Weisen(mit Zirkel) konstruieren: Den Kreis um Pkt.A
im−UhrZeigerSinn schlagen oder entgegen−UhrZeigerSinn .
Folgende Konstruktion:
Bild1 , Eukl-geo3.jpg
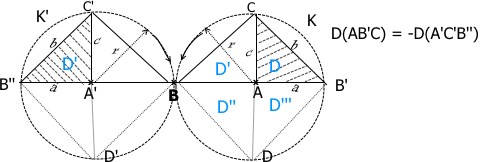
Im Bild gilt spez.Fall: a=c=r.
K und K' sind am Pkt.B gespiegelte, kongruente Kreise, die sich nur in
der Orientierung's Richtung, nämlich K' im UhrZeigerSinn und K entgegen,
unterscheiden. Wie bei den Dreiecken D,D' unterscheiden wir auch hier
wie folgt: K= -K' oder -K=K'.
Demzufolge stehen die zugehörigen Flächen zu sich in der Beziehung: F(K')= -F(K) oder F(K)= -F(K')
Auch die eingeschriebenen Dreiecke sind alle untereinander gespiegelt:
D' =-D ==> F(D') = -F(D)
D''=-D' ==> F(D'') = -F(D') = F(D)
D'''=-D'' ==> F(D''')= -F(D'') = -F(D)
D =-D''' ==> F(D) = -F(D''') = F(D)
Folgerung:
Die äußeren Eckpunkte der 4 Dreiecke (mit a=c) um Pkt.A teilen den vollen Kreisbogen in 4 gleiche Teile. Bei einer Längen-Teilung des vollen Kreisbogens in 360 gleiche Stücke würde die Kreisbogenlänge über den außeren Seiten b dann 90 betragen.
Def.1: Die Teilungs-Abschnitte werden als Grad° bezeichnet. Die 360° werden als Vollwinkel, die 90° Abschnitte als Rechter-Winkel und die 2 x 90°-Kreis-Abschnitte über der Strecke z.B. (BB') als gestreckter Winkel bezeichnet.
Def.2: Die Strecken (CD) und (BB') werden als Mittelsenkrechten, jeweils im Bezug auf die andere Strecke, bezeichnet, weil sie sich untereinander in rechten-Winkeln schneiden.
Folgerung1:
Da der allg. Kreis K(r>0) ein echtes 2-dim Linien-Objekt in der Ebene ist, wird als 2.Dimension, neben dem Radius, die "Orientierung" hinzugenommen. Nur im Fall r=0, entartet der Kreis zu einem Punkt der (Bogen)Länge NULL und ist somit dann kein 2-dim-geometr.Objekt der Ebene mehr!
Folgerung2:
Um vom Durchmesser des Kreises bei der Bemaßung eines Grades unabhängig zu sein, wird das Grad für den Einheits-Kreis(r=1) zu 1°=2π/360 im Bogenmaß festgelegt.
Folgerung3:
Um jeden Eckpunkt eines Dreieecks kann man einen Kreisbogen schlagen und den Öffnungs-Winkel der jeweils 2 abgehenden Strecken(Schenkel) bestimmen oder vergleichen.
Bild2 , Eukl-geo4.jpg

Folgerung4:
Im vorliegenden Fall der 4 gleichen Dreiecke D,D',D'',D''' (Bild1) erkennt man, dass alle Dreiecke im Pkt.A einen 90°-Winkel besitzen, auch wenn man den umschriebenen Kreis wegläßt und allg. c≠r setzt.
Def.3: Die Dreiecke mit den Eckpunkten (A,B,C) und einem Rechten-Winkel in einem der Eckpunkte heißen: rechtwinkliges Dreieck.
Folgende Konstruktion:

Demzufolge stehen die zugehörigen Flächen zu sich in der Beziehung: F(K')= -F(K) oder F(K)= -F(K')
Auch die eingeschriebenen Dreiecke sind alle untereinander gespiegelt:
D' =-D ==> F(D') = -F(D)
D''=-D' ==> F(D'') = -F(D') = F(D)
D'''=-D'' ==> F(D''')= -F(D'') = -F(D)
D =-D''' ==> F(D) = -F(D''') = F(D)
Folgerung:
Die äußeren Eckpunkte der 4 Dreiecke (mit a=c) um Pkt.A teilen den vollen Kreisbogen in 4 gleiche Teile. Bei einer Längen-Teilung des vollen Kreisbogens in 360 gleiche Stücke würde die Kreisbogenlänge über den außeren Seiten b dann 90 betragen.
Def.1: Die Teilungs-Abschnitte werden als Grad° bezeichnet. Die 360° werden als Vollwinkel, die 90° Abschnitte als Rechter-Winkel und die 2 x 90°-Kreis-Abschnitte über der Strecke z.B. (BB') als gestreckter Winkel bezeichnet.
Def.2: Die Strecken (CD) und (BB') werden als Mittelsenkrechten, jeweils im Bezug auf die andere Strecke, bezeichnet, weil sie sich untereinander in rechten-Winkeln schneiden.
Folgerung1:
Da der allg. Kreis K(r>0) ein echtes 2-dim Linien-Objekt in der Ebene ist, wird als 2.Dimension, neben dem Radius, die "Orientierung" hinzugenommen. Nur im Fall r=0, entartet der Kreis zu einem Punkt der (Bogen)Länge NULL und ist somit dann kein 2-dim-geometr.Objekt der Ebene mehr!
Folgerung2:
Um vom Durchmesser des Kreises bei der Bemaßung eines Grades unabhängig zu sein, wird das Grad für den Einheits-Kreis(r=1) zu 1°=2π/360 im Bogenmaß festgelegt.
Folgerung3:
Um jeden Eckpunkt eines Dreieecks kann man einen Kreisbogen schlagen und den Öffnungs-Winkel der jeweils 2 abgehenden Strecken(Schenkel) bestimmen oder vergleichen.

Folgerung4:
Im vorliegenden Fall der 4 gleichen Dreiecke D,D',D'',D''' (Bild1) erkennt man, dass alle Dreiecke im Pkt.A einen 90°-Winkel besitzen, auch wenn man den umschriebenen Kreis wegläßt und allg. c≠r setzt.
Def.3: Die Dreiecke mit den Eckpunkten (A,B,C) und einem Rechten-Winkel in einem der Eckpunkte heißen: rechtwinkliges Dreieck.
Aussagen über (rechtwinklige) Dreiecke:
1.
Zwei gleiche rechtwinklige Dreiecke, von denen eins um 180° gedreht
ist, und an der längsten Seite wieder zusammengefügt wird, ergeben ein sogenanntes
Rechteck, und die zusmmengefügten, längsten Dreiecksseiten heißen
Diagonale des Rechtecks.
2.
Def: Die Fläche eines Rechtecks wird formal mit dem
dem Produkt von 2 anliegenden Seiten des Rechteckes berechnet: F(Rechteck) = a * b
Folgerung: Die Fläche eines rechtwinkligen Dreiecks berechnet sich zu:
F = (a*b)/2 ,a,b sind die 2 kürzeren Seiten.
"Berechnen" ist hier symb. gemeint, weil den Strecken noch keine Zahlen zugeordnet
sind, siehe Abschnitt 1.6
F = (a*b)/2 ,
3.
Das nicht notwendigerweise rechtwinklige Dreieck ist mit 1 Winkel
und den Winkel-bildenten 2 Seiten eindeutig bestimmt.
1.2 Def. von Punkt und Gerade
Entspr. Axiom 2 entsteht der Punkt als Folge einer Strecke mit Länge NULL.
Anderseits entsteht ein Punkt auch bei der Konstruktion eines Kreises mit
Radius=NULL, wobei dieser entartete Kreis eine Bogenlänge NULL hat.
Beiden Betrachtungsweisen ist die Eigenschaft gemein, daß es sich um ein
Objekt der Ausdehung NULL handelt, beim Punkt die Länge und beim Kreis die
Fläche.
Def. Punkt: Der Punkt ist ein dimensions- und ausdehnungs- loses Object in jedem n-dim. Raum Rn ,n=1,2,3... . Dem Punkt wird deshalb formal die Dimension 0 zugeordnet.
Eine Gerade, Strecke oder allg. Linie von Pkt.A nach B ist von Haus aus ein Objekt der Ebene oder des Raumes, da es eine Längen-Ausdehnung >0 hat. Dazu folgende kontruktive Überlegung: A,B seien 2 verschiedene Punkte im Raum, dann kann man sich eine "Visier-Linie" von A nach B oder umgekehrt vorstellen, je nach dem, ob man hinter A oder B steht. Alle Punkte C zwischen A und B , die aus der "Visier-Linie" herausragen, kann man mit Pkt.A und B zu einem Dreieck verbinden, für dessen Abstände die Dreiecks_Ungleichung gilt, also: abs(AC)+abs(CB) > Visierlinie .
Def. Gerade: Gilt für 2 verschiedene Punkte A,B und jedem beliebigen weiteren Punkt P, P≠A und P≠B, die Dreickes-Ungleichung in der Form:
abs(AP) + abs(PB) = abs(AB) , dann heißt die Menge aller dieser Punkte P zuzüglich A,B Strecke oder Gerade zwischen A und B.
Bemerkung1:
Alle Objekte im Rn, die nur eine n-j dim. Ausdehnung im Rn besitzen, j<n , haben eine n-j dim. Ausdehnung =NULL. Beispiel: Linie im R³ hat Volumen =Fläche =0, trotz Len(Linie)>0.
Bemerkung2:
Der Punkt Null hat in allen Dimensionen die Ausdehnung NULL und ist deshalb überall gleich(identisch). Null= 0 =(0,0) = (0,...,0)!
Def. Punkt: Der Punkt ist ein dimensions- und ausdehnungs- loses Object in jedem n-dim. Raum Rn ,n=1,2,3... . Dem Punkt wird deshalb formal die Dimension 0 zugeordnet.
Eine Gerade, Strecke oder allg. Linie von Pkt.A nach B ist von Haus aus ein Objekt der Ebene oder des Raumes, da es eine Längen-Ausdehnung >0 hat. Dazu folgende kontruktive Überlegung: A,B seien 2 verschiedene Punkte im Raum, dann kann man sich eine "Visier-Linie" von A nach B oder umgekehrt vorstellen, je nach dem, ob man hinter A oder B steht. Alle Punkte C zwischen A und B , die aus der "Visier-Linie" herausragen, kann man mit Pkt.A und B zu einem Dreieck verbinden, für dessen Abstände die Dreiecks_Ungleichung gilt, also: abs(AC)+abs(CB) > Visierlinie .
Def. Gerade: Gilt für 2 verschiedene Punkte A,B und jedem beliebigen weiteren Punkt P, P≠A und P≠B, die Dreickes-Ungleichung in der Form:
abs(AP) + abs(PB) = abs(AB) , dann heißt die Menge aller dieser Punkte P zuzüglich A,B Strecke oder Gerade zwischen A und B.
Bemerkung1:
Alle Objekte im Rn, die nur eine n-j dim. Ausdehnung im Rn besitzen, j<n , haben eine n-j dim. Ausdehnung =NULL. Beispiel: Linie im R³ hat Volumen =Fläche =0, trotz Len(Linie)>0.
Bemerkung2:
Der Punkt Null hat in allen Dimensionen die Ausdehnung NULL und ist deshalb überall gleich(identisch). Null= 0 =(0,0) = (0,...,0)!
1.3 Senkrechte, Mittel-Senkrechte, Lot
Die Kontruktion von Senkrechte, Mittel-Senkrechte und Lot auf andere Strecken/
Geraden ist eine der zentralen Konstruktions-Prinzipien in der Eukl.Geometrie.
1. Senkrechte auf Gerade g in einem Pkt.A:
a) Um Pkt.A auf g einen Kreis(r=a) schlagen.Es entstehen 2 weitere Punkte P1, P2 auf g mit Pkt.A in der Mitte.
b) Mit Zirkelspanne(r=(P1,P2)=2a) je einen Kreis um Pkt.P1 und P2 schlagen. Beide Kreise schneiden sich in 2 weiteren Punkten C1,C2.
Bild , Eukl-geo7.jpg
2. Mittel-Senkrechte zwischen 2 Punkten P1,P2 auf Gerade g: a steht jetzt für die Strecke (P1,P2), also a=(P1,P2). Dann ergibt die Konstruktion zuvor ab 1.b) mit der Strecke (C1,C2) die gesuchte Mittel-Senkrechte in der Mitte zwischen P1 und P2!
3. Lot fällen von Punkt P ausserhalb Gerade g: Hier geht es darum, eine kürzeste Verbindung zwischen P und g zu konstruieren. Bei folgender Konstruktion erweist sich die kürzeste Verbindung als Senkrechte von P auf g.
a) Von pkt.P aus einen Kreisbogen mit einem Radius schlagen, der etwas über die Gerade g hinausgeht. Es entstehen 2 Punkte P1,P2 auf g.
b) Jetzt Konstruktion nach 2.(zuvor) durchführen. Die erhaltene Mittel-Senkrechte g2 schneidet g in einem neuen Pkt.A und geht gleichzeitig durch den Pkt.P. Somit ist die Strecke (P,A) das gesuchte Lot!
Bild , Eukl-geo8.jpg

1. Senkrechte auf Gerade g in einem Pkt.A:
a) Um Pkt.A auf g einen Kreis(r=a) schlagen.Es entstehen 2 weitere Punkte P1, P2 auf g mit Pkt.A in der Mitte.
b) Mit Zirkelspanne(r=(P1,P2)=2a) je einen Kreis um Pkt.P1 und P2 schlagen. Beide Kreise schneiden sich in 2 weiteren Punkten C1,C2.

2. Mittel-Senkrechte zwischen 2 Punkten P1,P2 auf Gerade g: a steht jetzt für die Strecke (P1,P2), also a=(P1,P2). Dann ergibt die Konstruktion zuvor ab 1.b) mit der Strecke (C1,C2) die gesuchte Mittel-Senkrechte in der Mitte zwischen P1 und P2!
3. Lot fällen von Punkt P ausserhalb Gerade g: Hier geht es darum, eine kürzeste Verbindung zwischen P und g zu konstruieren. Bei folgender Konstruktion erweist sich die kürzeste Verbindung als Senkrechte von P auf g.
a) Von pkt.P aus einen Kreisbogen mit einem Radius schlagen, der etwas über die Gerade g hinausgeht. Es entstehen 2 Punkte P1,P2 auf g.
b) Jetzt Konstruktion nach 2.(zuvor) durchführen. Die erhaltene Mittel-Senkrechte g2 schneidet g in einem neuen Pkt.A und geht gleichzeitig durch den Pkt.P. Somit ist die Strecke (P,A) das gesuchte Lot!

1.4 Verschieben, Drehen, Spiegeln, Zoomen
Die Gruppe der 4 Transformationen soll, (auch mit kontruktiven Mitteln),
Manipulationen geom.Objekte, (hier speziell in der Ebene), ermöglichen,
ohne die geom.Objekte zu verzerren, d.h., sie in ihrem geom.Aussehen
zu verändern. Beispiel: aus einer geraden Linie soll hinterher keine
krumme Linie werden. Das bedeutet bei einer Folge von Transformationen
aus dieser Gruppe müssen folg. Eigenschaften erhalten bleiben:
(Immer bezogen auf ein ganzes Objekt !)
- Winkel bleiben gleich
- Geraden bleiben Geraden
- Parallelität bleibt erhalten
- Kreisbögen bleiben Kreisbögen
Der Beweis dieser axiomatischen Aussagen entfällt, wegen Bemerkung3 im Abschnitt 1. Ausgangspunkt!
Das "Zoomen" steht steht hier für das Ähnlichkeits-Prinzip. Man kann sich das Vorstellen, wie einen Blick durch ein Fotoapparat. Näher rangehen heißt vergrößern, weiter weg verkleinern. Die Zoom- bzw. Ähnlichkeits-Transformation entsteht, wenn man alle Punkte des Rn mit einem reellen Faktor ≠0 multipliziert.
Bemerkung: In der Eukl.Geometrie macht sich die Multipl. mit Zoom-Faktor, z.B. f mit einer Strecke, durch Verlängerung der Strecke, f>1, oder durch Verkleinerung der Strecke, f kleiner 1, bemerkbar.
Allgemeine Aussage: Erkenntnis-Theoretisch sollen Objekte "aus der Nähe/Weite betrachtet" natürlich noch dieselben sein!
Bemerkung:
In der analyt.Geometrie wird dieses Prinzip durch sogenannte Lineare Transformationen gesichert.
Anschaulicher Beweis dieser Aussagen an Hand Dreieck:
Zunächst: Jedes Dreieck läßt sich in 2 rechtw.Dreiecke zerlegen.
Bild , Eukl-geo12.jpg
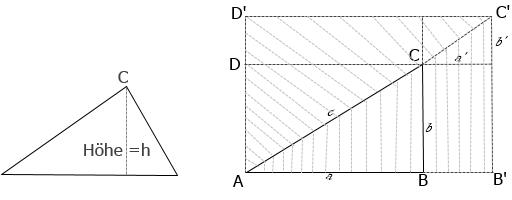
2.Teil: Im rechten Bild Fläche der schraffierten Dreiecke vergleichen (sind gleich):
untere Fläche: ab + a'b' + a'b
obere Fläche: = ab + a'b' + ab'
==> a'*b = a*b'
Wir setzen a'= f1 *a und b'= f2*b
==> (f1*a)*b = a*(f2*b)
Damit Gleichung erfüllt bleibt muß f1=f2 sein!
Zum Schluß prüfen, ob c' auch f*c ist:
Für c' gilt Pythagoras:
c'² = a'²+ b'²
= (f*a)² + (f*b)²
= f² * (a²+ b²)
1/f² * c'² = (a² + b²)
1/f² * c'² = c²
also ist: c'² = f² * c² und c' = f * c
-----------------------
Wir haben die Aussage zuvor nur für rechtwinkl. Dreiecke bestätigt. Da ein allg. Dreieck aber aus 2 recht. Dreiecken besteht, gilt diese Aussage auch für beliebige Dreiecke.
Ergebnis: Multiplikation mit Zahl erzeugt Ähnlichkeiten und umgekehrt!
Bemerkung1:
Die Gleichung a'*b = a*b' steht für ein Gleichgewichts-Prinzip, hier in der Geometrie für die Flächen-Gleichheit 2-er unterschidlicher Rechtecke. In der Mechanik spiegelt sie das Hebel-Gesetz wieder: Kraft*Kraftarm = Last*Lastarm, oder das Gleichgewicht von 2 Drehmomenten.
Bemerkung2:
Der wesentliche Unterschied zwischen Drehen u.Spiegeln ist: Drehung erfolgt immer um einen Punkt, gespiegelt wird dagegen an einer Strecke o.Gerade.
- Winkel bleiben gleich
- Geraden bleiben Geraden
- Parallelität bleibt erhalten
- Kreisbögen bleiben Kreisbögen
Der Beweis dieser axiomatischen Aussagen entfällt, wegen Bemerkung3 im Abschnitt 1. Ausgangspunkt!
Das "Zoomen" steht steht hier für das Ähnlichkeits-Prinzip. Man kann sich das Vorstellen, wie einen Blick durch ein Fotoapparat. Näher rangehen heißt vergrößern, weiter weg verkleinern. Die Zoom- bzw. Ähnlichkeits-Transformation entsteht, wenn man alle Punkte des Rn mit einem reellen Faktor ≠0 multipliziert.
Bemerkung: In der Eukl.Geometrie macht sich die Multipl. mit Zoom-Faktor, z.B. f mit einer Strecke, durch Verlängerung der Strecke, f>1, oder durch Verkleinerung der Strecke, f kleiner 1, bemerkbar.
Allgemeine Aussage: Erkenntnis-Theoretisch sollen Objekte "aus der Nähe/Weite betrachtet" natürlich noch dieselben sein!
Bemerkung:
In der analyt.Geometrie wird dieses Prinzip durch sogenannte Lineare Transformationen gesichert.
Anschaulicher Beweis dieser Aussagen an Hand Dreieck:
Zunächst: Jedes Dreieck läßt sich in 2 rechtw.Dreiecke zerlegen.

2.Teil: Im rechten Bild Fläche der schraffierten Dreiecke vergleichen (sind gleich):
untere Fläche: ab + a'b' + a'b
obere Fläche: = ab + a'b' + ab'
==> a'*b = a*b'
Wir setzen a'= f1 *a und b'= f2*b
==> (f1*a)*b = a*(f2*b)
Damit Gleichung erfüllt bleibt muß f1=f2 sein!
Zum Schluß prüfen, ob c' auch f*c ist:
Für c' gilt Pythagoras:
c'² = a'²+ b'²
= (f*a)² + (f*b)²
= f² * (a²+ b²)
1/f² * c'² = (a² + b²)
1/f² * c'² = c²
also ist: c'² = f² * c² und c' = f * c
-----------------------
Wir haben die Aussage zuvor nur für rechtwinkl. Dreiecke bestätigt. Da ein allg. Dreieck aber aus 2 recht. Dreiecken besteht, gilt diese Aussage auch für beliebige Dreiecke.
Ergebnis: Multiplikation mit Zahl erzeugt Ähnlichkeiten und umgekehrt!
Bemerkung1:
Die Gleichung a'*b = a*b' steht für ein Gleichgewichts-Prinzip, hier in der Geometrie für die Flächen-Gleichheit 2-er unterschidlicher Rechtecke. In der Mechanik spiegelt sie das Hebel-Gesetz wieder: Kraft*Kraftarm = Last*Lastarm, oder das Gleichgewicht von 2 Drehmomenten.
Bemerkung2:
Der wesentliche Unterschied zwischen Drehen u.Spiegeln ist: Drehung erfolgt immer um einen Punkt, gespiegelt wird dagegen an einer Strecke o.Gerade.
1.5 Parallelität von Geraden
Dies Problematik hat 2 Seiten, zum Einen Untersuchen, ob 2 gegebene
Geraden parallel sind, zum Anderen zu einer gegebenen Gerade eine zweite Gerade in
einem best. Abstand (zur 1.Gerade) konstruieren, die parallel zur Ersten ist.
Teil 1: Geg. 2 Geraden g1,g2 in der Ebene mit einem Pkt.P1 auf g1
a) von P1 aus eine Senkrechte in Richtung g2, entspr. Abschnitt 1.3, errichten, bis diese Senkrechte g2 in Pkt.P2 schneidet.
b) Jetzt umgekehrt von Pkt.P2 aus eine Senkrechte zurück zu g1 errichten, bis diese die Gerade g1 in Pkt.P1' schneidet.
Ergebnis: Ist P1=P1', dann sind g1 und g2 zueinander parallel!
Bild , Eukl-geo5.jpg

Teil 2: Geg. 1 Gerade g1 und Strecke c auf g1
a) 2 Punkte P1,P2 mit c=(P1,P2) auf g1 festlegen und in jedem Pkt. eine Senkrechte in die gleiche Richtung errichten.
b) Auf Senkrechten, von P1 und P2 aus, die Strecke c abtragen. Es enstehen die Punkte P1', P2' . c) Dann durch P1' und P2' eine Gerade g2 legen. Ergebnis: g2 is dann die Parallele zu g1 l!
Bild , Eukl-geo6.jpg

Diese Argumentation funktioniert so nur in der Ebene. Will man Parallelität ähnlich im R³ untersuchen, muß man zuvor sich alle Projektionen der Geraden in die Ebene anschauen: R³={x,y,z} ,R²={x,y};{y,z};{z,x}. In allen 2-dim-Unterräumen des R³ muß dann die Prüfung nach Teil1 vorgenommen werden.
Bemerkung2:
Eine weitere Möglichkeit der Parallelitäts-Prüfung wäre die mehrfache Anwendung der hier zulässigen Transformationen: Verschieben und Drehen. Ergebnis: Hat man Deckungs-Gleichheit erreicht, ohne die Operation Drehen, dann sind die Geraden parallel. "Verschieben" heißt deshalb auch in der Eukl.Geometrie "Parallel-Verschiebung". Diese Methode funktioniert übrigens auch in den Rn ,n>2 .
Bemerkung3:
Die Untersuchung von Paralellität in der Analyt.Geometrie erfolgt zweckmäßiger- weise über Skalar-Produkte.
Teil 1: Geg. 2 Geraden g1,g2 in der Ebene mit einem Pkt.P1 auf g1
a) von P1 aus eine Senkrechte in Richtung g2, entspr. Abschnitt 1.3, errichten, bis diese Senkrechte g2 in Pkt.P2 schneidet.
b) Jetzt umgekehrt von Pkt.P2 aus eine Senkrechte zurück zu g1 errichten, bis diese die Gerade g1 in Pkt.P1' schneidet.
Ergebnis: Ist P1=P1', dann sind g1 und g2 zueinander parallel!

Teil 2: Geg. 1 Gerade g1 und Strecke c auf g1
a) 2 Punkte P1,P2 mit c=(P1,P2) auf g1 festlegen und in jedem Pkt. eine Senkrechte in die gleiche Richtung errichten.
b) Auf Senkrechten, von P1 und P2 aus, die Strecke c abtragen. Es enstehen die Punkte P1', P2' . c) Dann durch P1' und P2' eine Gerade g2 legen. Ergebnis: g2 is dann die Parallele zu g1 l!

Diese Argumentation funktioniert so nur in der Ebene. Will man Parallelität ähnlich im R³ untersuchen, muß man zuvor sich alle Projektionen der Geraden in die Ebene anschauen: R³={x,y,z} ,R²={x,y};{y,z};{z,x}. In allen 2-dim-Unterräumen des R³ muß dann die Prüfung nach Teil1 vorgenommen werden.
Bemerkung2:
Eine weitere Möglichkeit der Parallelitäts-Prüfung wäre die mehrfache Anwendung der hier zulässigen Transformationen: Verschieben und Drehen. Ergebnis: Hat man Deckungs-Gleichheit erreicht, ohne die Operation Drehen, dann sind die Geraden parallel. "Verschieben" heißt deshalb auch in der Eukl.Geometrie "Parallel-Verschiebung". Diese Methode funktioniert übrigens auch in den Rn ,n>2 .
Bemerkung3:
Die Untersuchung von Paralellität in der Analyt.Geometrie erfolgt zweckmäßiger- weise über Skalar-Produkte.
1.6 Triangulation der Ebene
Gegeben Dreieck D(A,B,C). Dieses Dreieck Drehen um 180° im Mittelpunkt jeder Seite.
Es enstehen 3 neue Dreiecke.
1. Schritt: 3 x Drehen
Bild , Eukl-geo13.jpg
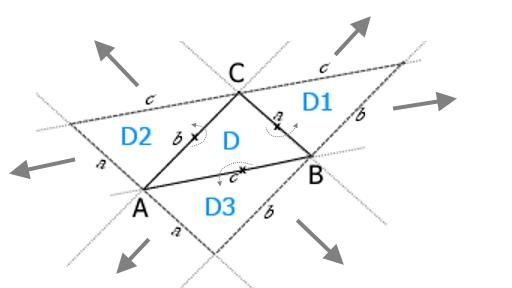
Mit den aussen liegenden Dreiecken, an den aussen lieg. Seiten, fortfahren. > 2 x 3 neue Dreiecke.
. . . . . . . . .
n. Schritt:
Mit den aussen liegenden Dreiecken, an den aussen lieg. Seiten, fortfahren. > n x 3 neue Dreiecke.
Ergebnis: bei n-> unendlich erhalten wir eine komplette, lückenlose Uberdeckung der Ebene mit identischen Dreiecken.
Bemerkung1:
Bei jeder Drehung bleibt die Orientierung des Dreiecks erhalten.
Bemerkung2:
Es können auch gleichseitige-Dreiecke verwendet werden, D(a,a,a).
Bemerkung3:
Die Dreiecke können auch paarweise zu Parallelogrammen zusammengefaßt werden. Dann erhält man ein Raster mit nur noch 2 Seiten, z.B. a,b.
Bemerkung4:
Wählt man gleichschenklige und rechtwinklige Dreiecke und faßt diese paarweise zu Quadraten zusammen, so erhält man quadrat.Raster der Ebene mit:
Raster-Höhe = Raster-Breite = a.
Bemerkung5:
Mit einer Rasterung lassen sich beliebige geometr.Objekte überdecken, so daß deren Flächen-Inhalt annähernd mit Raster-Elemnten ausgezählt werden können.
F(Objekt) ~ Anz.(innen-liegender-Elemente).
Fussnote: Der Grenzübergang -> ∞ ist in der Eukl.Geometrie eigentlich nicht zugelassen. Siehe dazu Abschnitt 1.11 Grenzübergänge
1. Schritt: 3 x Drehen

Mit den aussen liegenden Dreiecken, an den aussen lieg. Seiten, fortfahren. > 2 x 3 neue Dreiecke.
. . . . . . . . .
n. Schritt:
Mit den aussen liegenden Dreiecken, an den aussen lieg. Seiten, fortfahren. > n x 3 neue Dreiecke.
Ergebnis: bei n-> unendlich erhalten wir eine komplette, lückenlose Uberdeckung der Ebene mit identischen Dreiecken.
Bemerkung1:
Bei jeder Drehung bleibt die Orientierung des Dreiecks erhalten.
Bemerkung2:
Es können auch gleichseitige-Dreiecke verwendet werden, D(a,a,a).
Bemerkung3:
Die Dreiecke können auch paarweise zu Parallelogrammen zusammengefaßt werden. Dann erhält man ein Raster mit nur noch 2 Seiten, z.B. a,b.
Bemerkung4:
Wählt man gleichschenklige und rechtwinklige Dreiecke und faßt diese paarweise zu Quadraten zusammen, so erhält man quadrat.Raster der Ebene mit:
Raster-Höhe = Raster-Breite = a.
Bemerkung5:
Mit einer Rasterung lassen sich beliebige geometr.Objekte überdecken, so daß deren Flächen-Inhalt annähernd mit Raster-Elemnten ausgezählt werden können.
F(Objekt) ~ Anz.(innen-liegender-Elemente).
Fussnote: Der Grenzübergang -> ∞ ist in der Eukl.Geometrie eigentlich nicht zugelassen. Siehe dazu Abschnitt 1.11 Grenzübergänge
1.7 Messen und Vergleichen von Strecken
Entspr. Axiom2 sind wir bisher nur von Relationen zwischen Strecken
ausgegangen, z.B. über die Dreiecks-Ungleichung zu einem weiteren Pkt. oder
dem Verhältnis der 3 Seiten im rechtw. Dreieck zueinander (Pythagoras).
Um nun mit den Strecken auch direkt Rechnen zu können, wurde eine sogenannte Norm- bzw. Referenz-Strecke eingeführt, zwischen 2 willkürlich festgelegten Punkten P1,P2 , die die Namen: NULL=P1 und EINS=P2 bekamen. In der Folge bekam die Strecke(NULL,EINS) den Namen "Eins" und es wurde ihr die Zahl=1 zugeordnet:
Eins=(NULL,EINS), len(Eins)=abs(Eins)=1
Jetzt kann man jede Strecke (P1,P2) in der Ebene/Raum durch Drehen und Schieben in Richtung der Referenz-Eins-Strecke diese, (P1,P2)-Strecke, mit der Eins-Strecke so zur Deckung bringen, daß durch Multiplikation der Eins-Strecke mit einem Faktor f>0 die Eins-Strecke deckunsgleich (kongruent) mit der Strecke (P1,P2) wird.
Ergebnis: Ich kann die Längen jetzt vergleichen:
len(P1,P2) = len(Eins)*f = 1 *f = f
Def: Jeder Strecke a=(P1,P2), (P1,P2 Punkte der Ebene/Raum), wird als Länge die Zahl f zugeordnet, f nach vorherigem Algorithmus ermittelt. abs(a)=f
Bemerkung1:
In der Eukl.Geometrie tuen wir der Einfachheit halber den Namen der Strecke mit seiner Länge assoziieren. Sei a=(P1,P2), dann gelte:
len=(P1,P2) =len(P2,P1) =abs(P1,P2) =a
Folgerung:
Bei Zugrundelegung eines Rechteck-Rasters, siehe Abschnitt "Triangulation der Ebene", können die Flächen einfacher geom.Objekte (Dreiecke etc.), wie auch im Lokalen-Raum =Newton-Raum üblich, mit dem Vielfachen von x,y berechnet/bemaßt werden (x,y sind Seitenlängen des Rasters).
Bemerkung2:
Zur weiteren Vereinfachung und Handhabung können die Seiten des x,y-Raster, im Vergleich zur Referenzstrecke Eins, mit der Zahl 1 bemaßt werden (genormtes quadrat. Raster).
Um nun mit den Strecken auch direkt Rechnen zu können, wurde eine sogenannte Norm- bzw. Referenz-Strecke eingeführt, zwischen 2 willkürlich festgelegten Punkten P1,P2 , die die Namen: NULL=P1 und EINS=P2 bekamen. In der Folge bekam die Strecke(NULL,EINS) den Namen "Eins" und es wurde ihr die Zahl=1 zugeordnet:
Jetzt kann man jede Strecke (P1,P2) in der Ebene/Raum durch Drehen und Schieben in Richtung der Referenz-Eins-Strecke diese, (P1,P2)-Strecke, mit der Eins-Strecke so zur Deckung bringen, daß durch Multiplikation der Eins-Strecke mit einem Faktor f>0 die Eins-Strecke deckunsgleich (kongruent) mit der Strecke (P1,P2) wird.
Ergebnis: Ich kann die Längen jetzt vergleichen:
len(P1,P2) = len(Eins)*f = 1 *f = f
Def: Jeder Strecke a=(P1,P2), (P1,P2 Punkte der Ebene/Raum), wird als Länge die Zahl f zugeordnet, f nach vorherigem Algorithmus ermittelt. abs(a)=f
Bemerkung1:
In der Eukl.Geometrie tuen wir der Einfachheit halber den Namen der Strecke mit seiner Länge assoziieren. Sei a=(P1,P2), dann gelte:
len=(P1,P2) =len(P2,P1) =abs(P1,P2) =a
Folgerung:
Bei Zugrundelegung eines Rechteck-Rasters, siehe Abschnitt "Triangulation der Ebene", können die Flächen einfacher geom.Objekte (Dreiecke etc.), wie auch im Lokalen-Raum =Newton-Raum üblich, mit dem Vielfachen von x,y berechnet/bemaßt werden (x,y sind Seitenlängen des Rasters).
Bemerkung2:
Zur weiteren Vereinfachung und Handhabung können die Seiten des x,y-Raster, im Vergleich zur Referenzstrecke Eins, mit der Zahl 1 bemaßt werden (genormtes quadrat. Raster).
1.8 Kreise und Dreiecke
Satz1: 1.Teil: 3 paarweise verschiedenen Punkten auf einem Kreis lassen
sich immer zu einem Dreieck verbinden. Umgekehrt gilt auch: 2.Teil: Durch 3 Punkte
A,B,C, die verbunden kein entartetes Dreieck ergeben, kann man immer
einen Kreis konstruieren.
Beweis:
zu Teil1: trivial, Punkte verbinden.
zu Teil2: 2 Mittel-Senkrechten auf Strecke (A,C) und Strecke (B,C) errichten. Die Mittel-Senkrechten schneiden sich in einem Punkt M. Dieser Punkt ist Mittelpunkt eines Kreises der durch alle Punkte A,B,C geht.
Hilfssatz: die Mittel-Senkrechte einer Sekante geht durch den Kreis-Mittelpunkt.
Bild , Eukl-geo9.jpg
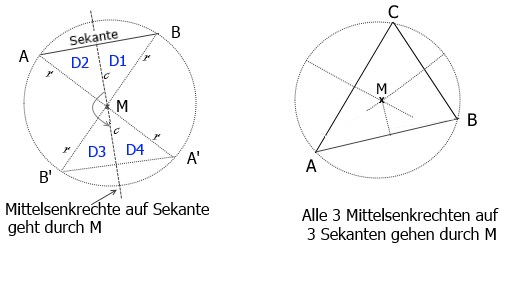
Ergebnis:
Alle Winkel um Teilungspkt. sind 90° und somit ist die neue Teilungs-Strecke gleichzeitig Mittel-Senkrechte auf Sekante!
Im rechten Bild sieht man, dass alle Verb.-Strecken zwischen 2 Punkten auf dem Kreis Sekanten sind und somit deren Mittel-Senkrechten durch M gehen, zusätzlich sind nach linkem Bild die Strecken (A,M) =(B,M) =(C,M) =Radius!
Ende des Beweises
Satz2: Ein beliebiger Kreis-Radius berührt den Kreisbogen in einem Punkt A. Die Senkrechte zum Radius im Pkt.A heißt: Tangente im Pkt.A des Kreises. 3 verschieden Punkte auf dem Kreis ergeben 3 verschieden Tangenten, die untereinander nicht parallel sind und sich deshalb, da sie gleichzeitig auch Geraden sind, entspr. Axiom1, in 3 Punkten schneiden, also über die Schnittpunkte ein Dreieck bilden.
Deshalb gilt umgekehrt: Zu jedem echten Dreieck gibt es einen sogenannten Dreiecks-Innenkreis, der die 3 Seiten des aussen liegenden Dreiecks in genau 3 Punkten berührt.
HilfsSatz: In einem rechtwinkligen Dreieck besteht zwischen den Seiten a,b,c folgende Relation: c² = a² + b² (Satz des Pythagoras):
Bild , Eukl-geo10.jpg
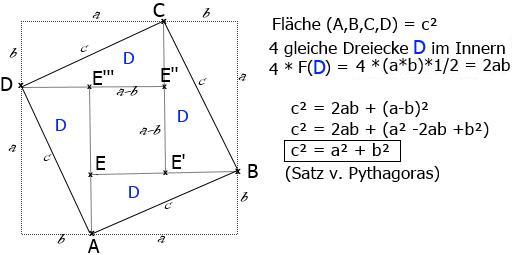
Bild , Eukl-geo11.jpg
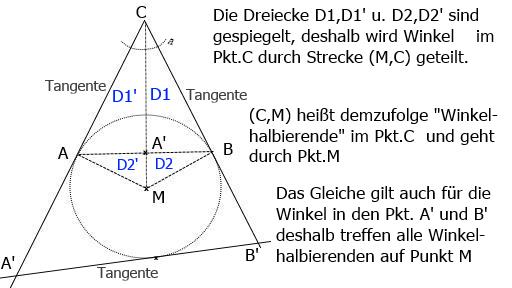
Die Winkelhalbierenden im Dreieck, hier (A',B',C), gehen alle durch einen Pkt.M im Innern des Dreiecks, nämlich dem Mittelpunkt des Dreieck-Innen-Kreises.
Ende des Beweises
Genauere Def. der Tangente, als Grenzübergang von Sekanten, siehe 1.11 Fläche Kreisscheibe.
Beweis:
zu Teil1: trivial, Punkte verbinden.
zu Teil2: 2 Mittel-Senkrechten auf Strecke (A,C) und Strecke (B,C) errichten. Die Mittel-Senkrechten schneiden sich in einem Punkt M. Dieser Punkt ist Mittelpunkt eines Kreises der durch alle Punkte A,B,C geht.
Hilfssatz: die Mittel-Senkrechte einer Sekante geht durch den Kreis-Mittelpunkt.

Ergebnis:
Alle Winkel um Teilungspkt. sind 90° und somit ist die neue Teilungs-Strecke gleichzeitig Mittel-Senkrechte auf Sekante!
Im rechten Bild sieht man, dass alle Verb.-Strecken zwischen 2 Punkten auf dem Kreis Sekanten sind und somit deren Mittel-Senkrechten durch M gehen, zusätzlich sind nach linkem Bild die Strecken (A,M) =(B,M) =(C,M) =Radius!
Satz2: Ein beliebiger Kreis-Radius berührt den Kreisbogen in einem Punkt A. Die Senkrechte zum Radius im Pkt.A heißt: Tangente im Pkt.A des Kreises. 3 verschieden Punkte auf dem Kreis ergeben 3 verschieden Tangenten, die untereinander nicht parallel sind und sich deshalb, da sie gleichzeitig auch Geraden sind, entspr. Axiom1, in 3 Punkten schneiden, also über die Schnittpunkte ein Dreieck bilden.
Deshalb gilt umgekehrt: Zu jedem echten Dreieck gibt es einen sogenannten Dreiecks-Innenkreis, der die 3 Seiten des aussen liegenden Dreiecks in genau 3 Punkten berührt.
HilfsSatz: In einem rechtwinkligen Dreieck besteht zwischen den Seiten a,b,c folgende Relation: c² = a² + b² (Satz des Pythagoras):


Die Winkelhalbierenden im Dreieck, hier (A',B',C), gehen alle durch einen Pkt.M im Innern des Dreiecks, nämlich dem Mittelpunkt des Dreieck-Innen-Kreises.
Genauere Def. der Tangente, als Grenzübergang von Sekanten, siehe 1.11 Fläche Kreisscheibe.
1.9 Zerlegung des Dreiecks in 2 rechtw.Dreiecke
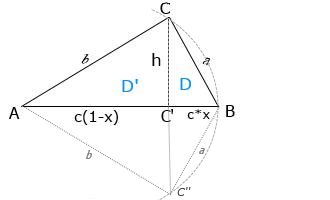
b) Die Höhe h teilt das Dreieck in 2 rechtw. Dreiecke mit einer Teilung einer Seite, z.B. c, wie in Bild, zwischen Pkt.A und Pkt.B. Für die Teilung von c benutzen wir einen Faktor x, x>0, wie folgt: c*(1-x) und c*x .
c) Für beide Dreiecke lautet die Fläche:
F(D) = h*c*x
F(D') = h*c*(1-x)
----------------------------
F(D+D') = h*(c*x - c*(1-x))
= h*c
d)Das Lot (C,C') kann auch wie folgt konstruiert werden: Dreieck (A,B,C) nach unten, um Strecke (A,B) spiegeln. Dann die Punkte C u.C'' verbinden.
Frage: In welcher Relation stehen h,x zu den bekannten Größen a,b,c ?
Lösung , Berechnen von x über Pythagoras:

x = 1/(2c²) *(c² +a² -b²) und
h² = a² - (1/(2c) *(c² +a² -b²))²
Hieraus kann man für ein gleichschenk.Dreieck, a=b, x=1/2 , d.h. die Höhe teilt das Dreieck in der Mitte, ableiten:
h² = a²-(1/(2c) *c²)² = a² -c²/4 = (a+c/2)*(a-c/2) .
Für ein gleichseitiges Dreieck: h² = a²(3/4). Weiter: sind alle a=1, dann ist Fläche
F(1,1,1) = h *1 = sqrt(3)/2 *1² .
Bemerkung:
Da im gleichseitiges Dreieck alle Winkel = 60° sind, hat man für die Relation h/a und a=1 den Winkel zu sin(60°)= sqrt(3)/2 bestimmt!
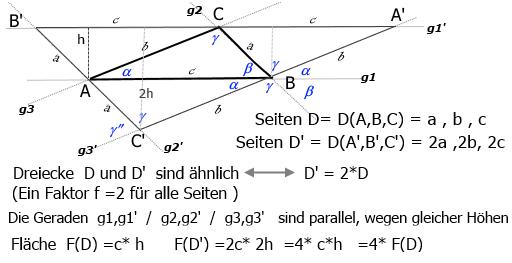
1.10 Winkelsummen im Dreieck
Drehen eines Dreieckecks D(A,B,C) um 180° um die Seiten-Mittelpunkte, je 1 mal:
Bild , Eukl-geo16.jpg
Winkelsumme:
Im Pkt.B gilt: Winkel 2α +2β +2γ =360° (Vollwinkel), also ∠A +∠B +∠C =180°
Zentri-Winkel:
Schneiden sich 2 Geraden z.B. in einem Pkt.B, dann sind gegenüber-liegende Winkel gleich, hier z.B. ∠a = ∠a
Neben-Winkel:
Schneiden sich 2 Geraden z.B. in einem Pkt.C', dann ergänzen sich nebeneinander- liegende Winkel auf einer Geraden, hier g3', zu: γ + γ'' =190°
Stufen-Winkel:
Wird eine Gerade, hier g3', von 2 parallelen Geraden in 2 Punkten, hier B und C', geschnitten entstehen sogenannte Stufen-Winkel:
Pkt.B(γ)=Pkt.C'(γ) ; Pkt.B(α+β)=Pkt.C'(γ'')
Zoom-Faktor
Man sieht hier sehr schön den Dualismus zwischen Ähnlichkeit und Zoom-Faktor, hier f=2.
Zusammenfassendes Beispiel zu Konstrukt. und Winkel:
Bild , Eukl-geo16a.jpg
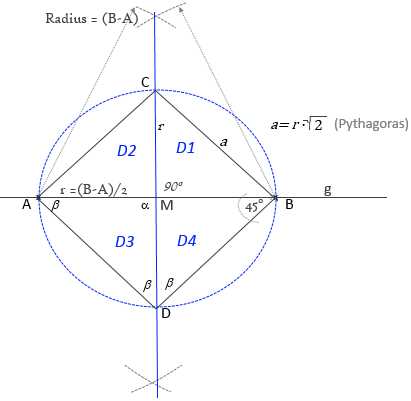
Ergebnis: Mittelsenkrechte zu (A,B), die Gerade g in M schneidet.
2. Um Pkt.M Voll-Kreisbogen schlagen mit r=0.5*Len(A,B). Es entstehen die Punkte C und D. Dann Punkte (A,B,C,D) verbinden.
Ergebnis: Es entsteht ein Viereck =Rechteck =Quadrat mit Seitenlänge a = sqrt(2)*r.
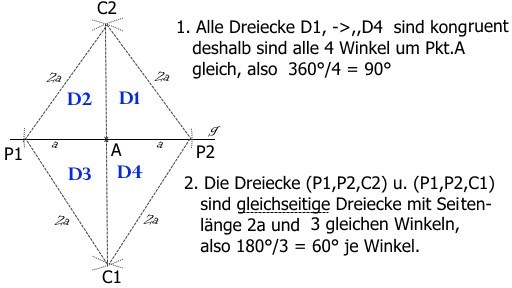
3. Dreiecke D1,D2,D3,D4 sind identisch, durch Drehung um Pkt M mit viertel-Vollkreis (90°) können sie jeweils zur Deckung gebracht werden.
4. Die Winkel um Pkt.M sind alle gleich (1/4*VollKreis =360°/4) , weil Dreiecke D1=D2=D3=D4 sind.
5. Da D1,D2,D3,D4 im Pkt.M gleichschenklige Dreiecke (Seiten=r) sind, sind die aussen liegenden Winkel β , in den Punkten A,B,C,D, ebenfalls gleich. Weil nebeneinander liegende Winkel β zusammen 90° ergeben (wegen Quadrat) , gilt:
2*β =90° , ==> β=45° und Winkel-Summe-Dreieck= 180°.
6. Die Winkel in den Eckpunkten liegen jeweils unter einem Halbkreis, der Teil des blauen Aussen-Kreises ist. Dies erfüllt den Tatbestand des Satzes von Thales : "Der Winkel unterm Halbkreis ist ein Rechter".

Winkelsumme:
Im Pkt.B gilt: Winkel 2α +2β +2γ =360° (Vollwinkel), also ∠A +∠B +∠C =180°
Zentri-Winkel:
Schneiden sich 2 Geraden z.B. in einem Pkt.B, dann sind gegenüber-liegende Winkel gleich, hier z.B. ∠a = ∠a
Neben-Winkel:
Schneiden sich 2 Geraden z.B. in einem Pkt.C', dann ergänzen sich nebeneinander- liegende Winkel auf einer Geraden, hier g3', zu: γ + γ'' =190°
Stufen-Winkel:
Wird eine Gerade, hier g3', von 2 parallelen Geraden in 2 Punkten, hier B und C', geschnitten entstehen sogenannte Stufen-Winkel:
Pkt.B(γ)=Pkt.C'(γ) ; Pkt.B(α+β)=Pkt.C'(γ'')
Zoom-Faktor
Man sieht hier sehr schön den Dualismus zwischen Ähnlichkeit und Zoom-Faktor, hier f=2.
Zusammenfassendes Beispiel zu Konstrukt. und Winkel:

Ergebnis: Mittelsenkrechte zu (A,B), die Gerade g in M schneidet.
2. Um Pkt.M Voll-Kreisbogen schlagen mit r=0.5*Len(A,B). Es entstehen die Punkte C und D. Dann Punkte (A,B,C,D) verbinden.
Ergebnis: Es entsteht ein Viereck =Rechteck =Quadrat mit Seitenlänge a = sqrt(2)*r.
3. Dreiecke D1,D2,D3,D4 sind identisch, durch Drehung um Pkt M mit viertel-Vollkreis (90°) können sie jeweils zur Deckung gebracht werden.
4. Die Winkel um Pkt.M sind alle gleich (1/4*VollKreis =360°/4) , weil Dreiecke D1=D2=D3=D4 sind.
5. Da D1,D2,D3,D4 im Pkt.M gleichschenklige Dreiecke (Seiten=r) sind, sind die aussen liegenden Winkel β , in den Punkten A,B,C,D, ebenfalls gleich. Weil nebeneinander liegende Winkel β zusammen 90° ergeben (wegen Quadrat) , gilt:
2*β =90° , ==> β=45° und Winkel-Summe-Dreieck= 180°.
6. Die Winkel in den Eckpunkten liegen jeweils unter einem Halbkreis, der Teil des blauen Aussen-Kreises ist. Dies erfüllt den Tatbestand des Satzes von Thales : "Der Winkel unterm Halbkreis ist ein Rechter".
1.11 Fläche der Kreisscheibe (mit Def.Tangente)
Die Fläche einer Kreisscheibe läßt sich mit den Mitteln der Eukl.Geometrie,
hier ist das "Messen und Vergleichen von Strecken" gemeint, nur angenähert
ermitteln.
Die Vorgehensweise ist: Ausschöpfung des inneren Kreises mit Dreiecken, entspr. Abschnitt "1.6 Triangulation der Ebene", dann n mal schrittweise Verkleinern der Dreiecke und zum Schluß der Grenzübergang n -> ∞ .
Bemerkung1: In der Eukl.Geometrie sind zwar Algorithmen mit beliebig vielen Schritten n erlaubt, aber n muß dabei immer kleiner unendlich bleiben!
Grenzübergänge n -> ∞ sind nur in der Theorie der Analyt.Geometrie und Analysis erlaubt. (ebensowenig im Lokalen-Raum =Newton-Raum )
Allg.Bemerkung:
Das Grundprinzip des Grenzüberganges ist, dass man nachweist, daß eine Aussage in n-Schritten (Arbeitsgänge, Transformationen, Operationen etc.) stimmt. Dann schliesst man daraus, daß die Aussage auch im Unenlichen (n =unendlich) stimmt. Beispiel: Man sagt ein Abstand zwischen 2 Punkten wird (durch Transformationen) von Schritt zu Schritt kleiner, dann kann man sagen: für n=∞ ist der Abstand=NULL.
Bei folg. anschaulicher Beweisführung greifen wir auf Elemente der Analysis zurück.
Satz: F(K(Radius=r)) = pi * r²
anschauliche Beweisführung:
Wir beginnen mit einer 8-Teilung des Kreisbogen der Länge 2*pi*r, siehe Axiom3, und erhalten 8 gleiche Dreiecke:
Bild , Eukl-geo17.jpg
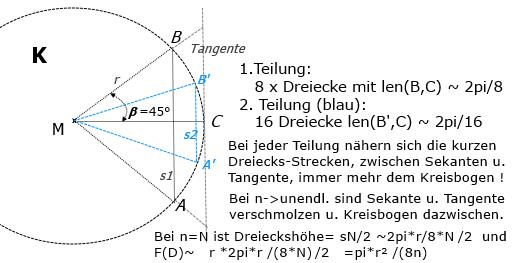
F(D)~ r *Bog.len/2 =r *[2pi*r/(8*n)]/2 =>
F(K)~ 8n*F(D) = 2pi*r²/2 *8n/8n = pi*r²
Bei jedem Schritt wird die Länge der Dreiecks-Basis auf (M,C) immer größer und nähert sich dem Radius=r an. Da der zugehörige Kreisbogen-Abschnitt komplett zwischen Sekante und Tangente liegt, kann man bei
n=∞ , F(K) = pi*r² setzen.
Ende des anschaulichen Beweises
Bemerkung2: Die Sekanten sn rücken schrittweise immer näher an die "Tangente". Die dabei entstehenden Dreiecke D(M.C,B') und D(M,C,A') sind gespiegelt, weshalb die Sekanten (B',A') senkrecht auf der Strecke (M,C)=Radius steht. Mit jedem Schritt wird die Sekanten-Länge kürzer. Für n=∞ ist len(sn)=0 , weshalb abs(B',A')=0 ist, und nach Axiom2 B'=A' ist und s∞ zur Tangente mutiert.
Def: Die Tangente ist eine entartete Sekante, die den Kreisbogen nur noch in einem Pkt. schneidet /berührt.
Die Vorgehensweise ist: Ausschöpfung des inneren Kreises mit Dreiecken, entspr. Abschnitt "1.6 Triangulation der Ebene", dann n mal schrittweise Verkleinern der Dreiecke und zum Schluß der Grenzübergang n -> ∞ .
Bemerkung1: In der Eukl.Geometrie sind zwar Algorithmen mit beliebig vielen Schritten n erlaubt, aber n muß dabei immer kleiner unendlich bleiben!
Grenzübergänge n -> ∞ sind nur in der Theorie der Analyt.Geometrie und Analysis erlaubt. (ebensowenig im Lokalen-Raum =Newton-Raum )
Allg.Bemerkung:
Das Grundprinzip des Grenzüberganges ist, dass man nachweist, daß eine Aussage in n-Schritten (Arbeitsgänge, Transformationen, Operationen etc.) stimmt. Dann schliesst man daraus, daß die Aussage auch im Unenlichen (n =unendlich) stimmt. Beispiel: Man sagt ein Abstand zwischen 2 Punkten wird (durch Transformationen) von Schritt zu Schritt kleiner, dann kann man sagen: für n=∞ ist der Abstand=NULL.
Bei folg. anschaulicher Beweisführung greifen wir auf Elemente der Analysis zurück.
Satz: F(K(Radius=r)) = pi * r²
anschauliche Beweisführung:
Wir beginnen mit einer 8-Teilung des Kreisbogen der Länge 2*pi*r, siehe Axiom3, und erhalten 8 gleiche Dreiecke:

F(D)~ r *Bog.len/2 =r *[2pi*r/(8*n)]/2 =>
F(K)~ 8n*F(D) = 2pi*r²/2 *8n/8n = pi*r²
Bei jedem Schritt wird die Länge der Dreiecks-Basis auf (M,C) immer größer und nähert sich dem Radius=r an. Da der zugehörige Kreisbogen-Abschnitt komplett zwischen Sekante und Tangente liegt, kann man bei
n=∞ , F(K) = pi*r² setzen.
Bemerkung2: Die Sekanten sn rücken schrittweise immer näher an die "Tangente". Die dabei entstehenden Dreiecke D(M.C,B') und D(M,C,A') sind gespiegelt, weshalb die Sekanten (B',A') senkrecht auf der Strecke (M,C)=Radius steht. Mit jedem Schritt wird die Sekanten-Länge kürzer. Für n=∞ ist len(sn)=0 , weshalb abs(B',A')=0 ist, und nach Axiom2 B'=A' ist und s∞ zur Tangente mutiert.
Def: Die Tangente ist eine entartete Sekante, die den Kreisbogen nur noch in einem Pkt. schneidet /berührt.
1.12 Allg. geometr. Objekte
Bei den folg. Betrachtungen gehen wir wieder von einem streng konstuktiven
Ansatz aus, auf der Basis der in Abschnitt "1.Ausgangspunkt" festgelegten Axiomen 1-3.
Wir verwenden für die Bemaßung von Strecken, siehe Abschnitt 1.7, die Symbolik:
Länge der Strecke (A,B) = Abstand der Punkte A,B voneinander = abs(A,B). abs(A,B) ist dann, in diesem Kontext, eine Zahl≠0, =0 nur dann, wenn A=B ist.
Definition δ-Umgebung:
K(P,r) sei Kreis um einen Pkt.P mit Radius=r, r>0, dann liegen alle Punkte A mit abs(A,P)>r ausserhalb des Kreises und bei abs(A,P)<r liegen alle Punkte A innerhalb des Kreises.
Pkt.B sei weiterer Punkt, abs(B,P)<r und B≠A , dann gelten für die 3 Punkte A,B,P und deren Abstände a=abs(A,P), b=abs(B,P) folg. Aussagen:
Aussage1: Sei b≤a und b+abs(B,A) =a , dann liegt B auf der Strecke zwischen (A,P). Zum Beweis siehe Abschnitt 1.0 Dreieck.
Aussage2: In Verallg. zu Aussage1 gilt: Um einen inneren Pkt. der δ-Umgebung kann man wiederum eine zweite δ-Umgebung legen, die vollständig in der ersten δ-Umgebung enthalten ist.
Symb.: δ1 > δ2 >0 , dann ist Uδ2(P2) ⊂ Uδ1(P1), wenn P2 ∈ Uδ1(P1) ist.
(Die δ-Umgeb. zu P2 ist vollst.enthalten in δ-Umgeb. zu P1 , wenn P2 Element von δ-Umgeb. zu P1 ist)
Bild , Eukl-geo18.jpg

Algorithmus: Zu einer Folge von n-δ-Umgeb., bei der jede δ-Umgeb. in der Vorigen enthalten sei, gibt es dann in der Ersten δ-Umgeb., Uδ1(P1), n * m Punkte.
Bei Grenzübergang n->∞ gibt es dann unendlich viele Punkte in der Uδ1(P1) -Umgebung. Daraus folgt:
In jeder δ-Umgeb. zu jedem Pkt. der Ebene, (kann auch Gerade o. Raum sein), gibt es unendlich viele weitere Punkte. Deshalb gilt:
Def.: Jeder Punkt ist Häufungspunkt ! Dies steht im Einklang mit Axiom2, da die Abstände von Punkten durchaus gegen Null streben können.
Um jetzt mit allg.geom.Objekten und den zugelassenen Transformationen:
- Verschieben
- Drehen
- Umklappen/Spiegeln
- Zoomen
ein vernünftiges Ergebnis, d.h. wiederum ein allg.geom.Objekt, zu erzielen, muß man an solche Objekte folg.Forderungen stellen:
- Abgrenzung, d.h. die Punkte haben endl.Abstände.
- Orientierung, d.h. die Pkte. können nach innen-und aussen-liegend unterschieden werden.
- Offen, d.h. die Ränder gehören nicht dazu.
Bespiel:
Bild , Eukl-geo19.jpg
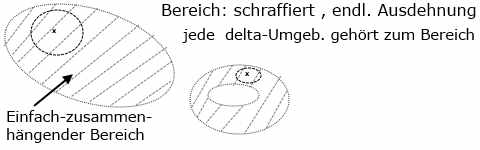
Fläche_Volumen(Rand) =0
Fläche(einf.zus.Bereich) =Fläche(kompakt.Bereich).
Folgerung2: Betrachtet man eine Folge von n-δ-Umgeb. Uδi(Pi), δ1 ≤ ... δi ≤ ... δn , und Punkte Ai mit:
δi/2 ≤ abs(Ai,Pi) < δi , die alle auf einer Geraden durch P1 liegen, dann haben die Pi alle Abstände untereinander, die ≥ δ1/2 sind. Nach n-Schritten hat der letzte Pkt Pn einen Abstand ≥n*δ1/2 von P1. Bei Grenzübergang n->∞ hat der Letzte Pkt., den es nur im Unendlichen gibt, den Abstand ∞ von P1. Da auch der letzte Punkt vor Unendlich eine δ-Umgeb. hat kann man definieren:
Def.: Die Ebene (auch Gerade /Raum usw,) kann durch δ-Umgebungen lückenlos, überlappend überdeckt werden. Dadurch ist der m-dim. Eukl.Raum ein offener Raum, also ein zulässiger einf.zus.Bereich, und kann deshalb insgesamt als Quell-Bereich für Transformationen /Abbildungen verwendet werden!
Unendlichkeits-Prinzip: Hat man eine Menge von n-Elemente, und man kann immer noch ein n+1.tes Element hinzufügen, dann ist die Anzahl, Länge, Zeitdauer etc. "unendlich" !
Länge der Strecke (A,B) = Abstand der Punkte A,B voneinander = abs(A,B). abs(A,B) ist dann, in diesem Kontext, eine Zahl≠0, =0 nur dann, wenn A=B ist.
Definition δ-Umgebung:
K(P,r) sei Kreis um einen Pkt.P mit Radius=r, r>0, dann liegen alle Punkte A mit abs(A,P)>r ausserhalb des Kreises und bei abs(A,P)<r liegen alle Punkte A innerhalb des Kreises.
Pkt.B sei weiterer Punkt, abs(B,P)<r und B≠A , dann gelten für die 3 Punkte A,B,P und deren Abstände a=abs(A,P), b=abs(B,P) folg. Aussagen:
Aussage1: Sei b≤a und b+abs(B,A) =a , dann liegt B auf der Strecke zwischen (A,P). Zum Beweis siehe Abschnitt 1.0 Dreieck.
Aussage2: In Verallg. zu Aussage1 gilt: Um einen inneren Pkt. der δ-Umgebung kann man wiederum eine zweite δ-Umgebung legen, die vollständig in der ersten δ-Umgebung enthalten ist.
Symb.: δ1 > δ2 >0 , dann ist Uδ2(P2) ⊂ Uδ1(P1), wenn P2 ∈ Uδ1(P1) ist.
(Die δ-Umgeb. zu P2 ist vollst.enthalten in δ-Umgeb. zu P1 , wenn P2 Element von δ-Umgeb. zu P1 ist)

Algorithmus: Zu einer Folge von n-δ-Umgeb., bei der jede δ-Umgeb. in der Vorigen enthalten sei, gibt es dann in der Ersten δ-Umgeb., Uδ1(P1), n * m Punkte.
Bei Grenzübergang n->∞ gibt es dann unendlich viele Punkte in der Uδ1(P1) -Umgebung. Daraus folgt:
In jeder δ-Umgeb. zu jedem Pkt. der Ebene, (kann auch Gerade o. Raum sein), gibt es unendlich viele weitere Punkte. Deshalb gilt:
Def.: Jeder Punkt ist Häufungspunkt ! Dies steht im Einklang mit Axiom2, da die Abstände von Punkten durchaus gegen Null streben können.
Um jetzt mit allg.geom.Objekten und den zugelassenen Transformationen:
- Verschieben
- Drehen
- Umklappen/Spiegeln
- Zoomen
ein vernünftiges Ergebnis, d.h. wiederum ein allg.geom.Objekt, zu erzielen, muß man an solche Objekte folg.Forderungen stellen:
- Abgrenzung, d.h. die Punkte haben endl.Abstände.
- Orientierung, d.h. die Pkte. können nach innen-und aussen-liegend unterschieden werden.
- Offen, d.h. die Ränder gehören nicht dazu.
Bespiel:

Fläche_Volumen(Rand) =0
Fläche(einf.zus.Bereich) =Fläche(kompakt.Bereich).
Folgerung2: Betrachtet man eine Folge von n-δ-Umgeb. Uδi(Pi), δ1 ≤ ... δi ≤ ... δn , und Punkte Ai mit:
δi/2 ≤ abs(Ai,Pi) < δi , die alle auf einer Geraden durch P1 liegen, dann haben die Pi alle Abstände untereinander, die ≥ δ1/2 sind. Nach n-Schritten hat der letzte Pkt Pn einen Abstand ≥n*δ1/2 von P1. Bei Grenzübergang n->∞ hat der Letzte Pkt., den es nur im Unendlichen gibt, den Abstand ∞ von P1. Da auch der letzte Punkt vor Unendlich eine δ-Umgeb. hat kann man definieren:
Def.: Die Ebene (auch Gerade /Raum usw,) kann durch δ-Umgebungen lückenlos, überlappend überdeckt werden. Dadurch ist der m-dim. Eukl.Raum ein offener Raum, also ein zulässiger einf.zus.Bereich, und kann deshalb insgesamt als Quell-Bereich für Transformationen /Abbildungen verwendet werden!
Unendlichkeits-Prinzip: Hat man eine Menge von n-Elemente, und man kann immer noch ein n+1.tes Element hinzufügen, dann ist die Anzahl, Länge, Zeitdauer etc. "unendlich" !
1.13 Teilung der Eins-Strecke und Rationale Zahlen
Def.: natürliche Zahlen N seien Repräsentanten für die Anzahl Elemente
in abzählbaren Mengen. Also:
n=1 steht für alle Mengen mit Anz=1
n=2 steht für alle Mengen mit Anz=2
... usw.
Def.: n=0 steht für die Null-Menge, die keine natürliche Menge ist, sondern erst durch Subtraktion entsteht, wenn von einer Menge m alle Elemente abgezogen werden!
Def.: Die ganzen Zahlen G umfassen die natürlichen Zahlen N und Null und negative ganze Zahlen, die entstehen, wenn von einer natürl.Zahl n1 eine andere Zahl n2 abgezogen wird, also n1-n2 und n2>n1 ist.
In der Menge G kann man umfassend Add./Sub. sowie Multiplizieren und Dividieren, wenn das ohne Rest möglich ist.
Potenzreihen-Darstellung eines Eins-Elementes:
Bild , Eukl-geo20.jpg

1 = 9/101 + 9/102 + 9/103 + ...
Allg. gilt für b-Teilung, b ganz >1 :
1 = (b-1)/b1 + (b-1)/b2 + (b-1)/b3 + ... oder
1/(b-1) = 1/b1 + 1/b2 + . . .
Dadurch können wir wie folgt definieren:
Def. rationale Zahlen: Alle Rationalen Zahlen R = p/q lassen sich als Potenzreihe in der Form:
p/(q-1) = p/q1 + p/q2 + p/q3 + + . . . darstellen
Folgerung1: Eine echt gebroch.rationale Zahl z läßt sich in dez.Schreibweise darstellen:
z = p(-n)/10-n + ... + p(-1)/10-1 + p(1)/10+1 + ... + p(m)/10+m
also eine endl. Potenzreihe. Die p(+i) stehen für die Ziffern vor dem Komma, und die p(-i) für die Ziffern nach dem Komma (Beispiel 23,645).
z= a +b, a ganz, b=0,xxx..xx ,n sei Anz. der "x" nach Komma, dann ist b*10n= ganze Zahl und b ist rat.Zahl in Form: b=ganze Zahl/10n .
Beispiel: b= 0,645 , b*103 =645 ,==> b=645/1000 =rat.Zahl p/q.
Satz: Es gilt: jede endl.Dez.Zahl der Form 0,xxx..xx ist eine Rationale Zahl, zusätzlich auch unendl. Dez.Zahlen mit Periode.
Beweis:
1. z = 0,xxx..xxpppp , ab n-Stellen nach Komma m-stellige Periode pppp bis ∞ , z = z * 10n bilden, jetzt steht m-stell. Periode gleich nach Komma.
2. z' = z* 10m jetzt ist z'=pppp,pppp pppp ->∞ mit einer Periode vor Komma.
3. z'-z = pppp , z' ersetzen: z* 10m -z = 9999
==> z(10m-1) =9999 und z=9999/(10m-1) =p/q
Ende des Beweises
Folgerung2: Nicht Rationale Zahlen wären im Umkehrschluß alle unendl. Dez.Zahlen (nach Komma), die nicht periodisch sind, oder anders gesagt, eine unendl. Periode haben:
r = p(-∞)/10-∞ +... p(1)/10+1 + ... p(m)/10+m
r = a,p1p2p3....p∞ (nicht periodisch)
Diese nicht Rat.Zahlen heißen irrationale Zahlen.
Beispiel:
Die Diagonale d des Quadrates mit Seitenlänge 1 hat nach Pythagoras die Länge d² =2 , d ist eine irrationale Zahl!
Beweis indirekt: angenommen d wäre doch rat.Zahl, dann müßte 2=p*p/(q*q) gelten. Es muß p>q>0 sein
1.Schritt: p=0+2, q=0+1 ==> [(0+2)/(0+1)]² =2/1² =4,00
2.Schritt: p=1+2, q=1+1 ==> [(1+2)/(1+1)]² =3/2² =2,25
3.Schritt: p=2+2, q=2+1 ==> [(2+2)/(2+1)]² =4/3² =1,77
. . . . .
n.Schritt: p=n-1+2, q=n-1+1 ==> [(n+1)/(n)]²
n+1.Schr.: p = n+2 , q = n+1 ==> [(n+2)/(n+1]²
Abschätzen: [(n+1)/n] / [(n+2)/(n+1)]
==> (n+1)(n+1) /(n+2)n
==> (n² +2n +1) /(n² +2n) =größer 1
Jeder Schritt n+1 ist kleiner als Schritt n .
Da die ersten 3 Schritte nicht stimmen und alle Folgeschritte < 1,77 sind, stimmt die Gleichung 2=p*p/(q*q) nicht und die Annahme ist falsch, also die Diagonale d in d²=2 ist eine irrationale Zahl.
Ende Beweis indirekt
n=1 steht für alle Mengen mit Anz=1
n=2 steht für alle Mengen mit Anz=2
... usw.
Def.: n=0 steht für die Null-Menge, die keine natürliche Menge ist, sondern erst durch Subtraktion entsteht, wenn von einer Menge m alle Elemente abgezogen werden!
Def.: Die ganzen Zahlen G umfassen die natürlichen Zahlen N und Null und negative ganze Zahlen, die entstehen, wenn von einer natürl.Zahl n1 eine andere Zahl n2 abgezogen wird, also n1-n2 und n2>n1 ist.
In der Menge G kann man umfassend Add./Sub. sowie Multiplizieren und Dividieren, wenn das ohne Rest möglich ist.
Potenzreihen-Darstellung eines Eins-Elementes:

1 = 9/101 + 9/102 + 9/103 + ...
Allg. gilt für b-Teilung, b ganz >1 :
1 = (b-1)/b1 + (b-1)/b2 + (b-1)/b3 + ... oder
1/(b-1) = 1/b1 + 1/b2 + . . .
Dadurch können wir wie folgt definieren:
Def. rationale Zahlen: Alle Rationalen Zahlen R = p/q lassen sich als Potenzreihe in der Form:
p/(q-1) = p/q1 + p/q2 + p/q3 + + . . . darstellen
Folgerung1: Eine echt gebroch.rationale Zahl z läßt sich in dez.Schreibweise darstellen:
z = p(-n)/10-n + ... + p(-1)/10-1 + p(1)/10+1 + ... + p(m)/10+m
also eine endl. Potenzreihe. Die p(+i) stehen für die Ziffern vor dem Komma, und die p(-i) für die Ziffern nach dem Komma (Beispiel 23,645).
z= a +b, a ganz, b=0,xxx..xx ,n sei Anz. der "x" nach Komma, dann ist b*10n= ganze Zahl und b ist rat.Zahl in Form: b=ganze Zahl/10n .
Beispiel: b= 0,645 , b*103 =645 ,==> b=645/1000 =rat.Zahl p/q.
Satz: Es gilt: jede endl.Dez.Zahl der Form 0,xxx..xx ist eine Rationale Zahl, zusätzlich auch unendl. Dez.Zahlen mit Periode.
Beweis:
1. z = 0,xxx..xxpppp , ab n-Stellen nach Komma m-stellige Periode pppp bis ∞ , z = z * 10n bilden, jetzt steht m-stell. Periode gleich nach Komma.
2. z' = z* 10m jetzt ist z'=pppp,pppp pppp ->∞ mit einer Periode vor Komma.
3. z'-z = pppp , z' ersetzen: z* 10m -z = 9999
==> z(10m-1) =9999 und z=9999/(10m-1) =p/q
Folgerung2: Nicht Rationale Zahlen wären im Umkehrschluß alle unendl. Dez.Zahlen (nach Komma), die nicht periodisch sind, oder anders gesagt, eine unendl. Periode haben:
r = p(-∞)/10-∞ +... p(1)/10+1 + ... p(m)/10+m
r = a,p1p2p3....p∞ (nicht periodisch)
Diese nicht Rat.Zahlen heißen irrationale Zahlen.
Beispiel:
Die Diagonale d des Quadrates mit Seitenlänge 1 hat nach Pythagoras die Länge d² =2 , d ist eine irrationale Zahl!
Beweis indirekt: angenommen d wäre doch rat.Zahl, dann müßte 2=p*p/(q*q) gelten. Es muß p>q>0 sein
1.Schritt: p=0+2, q=0+1 ==> [(0+2)/(0+1)]² =2/1² =4,00
2.Schritt: p=1+2, q=1+1 ==> [(1+2)/(1+1)]² =3/2² =2,25
3.Schritt: p=2+2, q=2+1 ==> [(2+2)/(2+1)]² =4/3² =1,77
. . . . .
n.Schritt: p=n-1+2, q=n-1+1 ==> [(n+1)/(n)]²
n+1.Schr.: p = n+2 , q = n+1 ==> [(n+2)/(n+1]²
Abschätzen: [(n+1)/n] / [(n+2)/(n+1)]
==> (n+1)(n+1) /(n+2)n
==> (n² +2n +1) /(n² +2n) =größer 1
Jeder Schritt n+1 ist kleiner als Schritt n .
Da die ersten 3 Schritte nicht stimmen und alle Folgeschritte < 1,77 sind, stimmt die Gleichung 2=p*p/(q*q) nicht und die Annahme ist falsch, also die Diagonale d in d²=2 ist eine irrationale Zahl.
1.14 Rationale Zahlen als Repräsentant von Potenzreihen und umgekehrt
in Abschnitt 1.13 zuvor hatten wir festgestellt, dass jede Dez.Zahlen-Darstellung
(endl. Ziffernfolge oder unendl. nur durch Periode) eine rat. Zahl p/q darstellt.
Umgekehrt gilt auch: jede Zahl p/q kann durch einen elementaren Algorithmus (bereits in der Schule bekannt) in eine Dez.Zahlen-Darstellung umgewandelt werden:
Bild , Eukl-geo21.jpg

z = 0* 100 +r1 10-1 . . . +rm 10-m
z = 0,r1r2 . . . rm
Satz1: Alle rationalen Zahlen r =p/q lassen sich als Potenzreihe der Form r =p *( (q+1)-1 +... +(q+1)-∞ ) darstellen.
Beweis: wegen Teilung des Eins-Elementes (z.B. b-Teilung, b natürl. Zahl), 1 *(b-1)= 1/b1 +1/b2 + . . . , siehe Abschnitt 1.13 zuvor, kann man durch setzen von b= (q+1)/p in Gleichung zuvor, diese umformen zu:
p/q = p/(q+1)1 +p/(q+1)2 + . . .
Ende des Beweises
Folgerung zu Satz1: Die Partialsummen der Potenzreihe im Satz1 bilden eine konvergente Folge. Deshalb kann man feststellen: Alle rat.Zahlen sind Grenzwert einer konvergenten Folge, also Häufungspunkt in der Menge der Zahlen.
Bemerkung1: In der Folgerung2 im Abschnitt 1.13 zuvor hatten wir unendl. Potenreihen (aus Ganzen Z. =rat.Zahlen) angegeben, die sich nicht in rat.Zahlen p/q umwandeln lassen. Diese hießen "irrationale Zahlen", und als Beispiel hatten wir die Diagonale d eines 1-Quadrates genannt, d²=2.
Der Vollständigkeit halber sei hier eine Potenzreihen -Entwicklung für d angegeben:
d= 1 +(0.5*ln2)1/1! + ... +(0.5*ln2)n/n! +....
davon: 0.7~ ln2= 1 -1/2 +1/3 + ... +(-1)(n+1) 1/n + . .
Algorithmus zur Ermittlung der wahren Länge eines Abstandes:
Sei d ein beliebiger Abstand und E das aktive Referenz-Eins-Element.
1.Schritt Im ersten Schritt ermitteln wir, wieviel mal d von E vollständig überdeckt wird (a'=a'*E). Dabei zerfällt a' in a +1, weil das letzte E i.a. darüber hinaus ragt (ansonsten ist Ermittlung zu Ende und a'=a ist ganze Zahl). Das letzte E bezeichnen wir als R (Rest). Beim nachfolg. Zyklus geht es genau um diesen Rest, der sukzessive entsteht, wenn wir E schrittweise teilen (Zoomfaktor f=10).
n.Schritt En = En-1/10 bilden und ermitteln, wieviel man R von En überdeckt wird (a'=a* En). Das besondere in diesen Teilungs-Schritten ist, dass a jetzt nicht mehr als ganze Zahl von 1-10 betrachtet wird, sondern als Index der 10-Teil-Abschnitte:
symb.:
x[n]i=i , n=Anz.der Zoom-Schritte, i=Index(0..9).
Wenn das k-te-En über R hinausragt, wird i=k-1 gesetzt, und es
geht mit Zyklus n+1 weiter. Ansonsten ragt R nicht über k-tes-En hinaus,
schließt also exakt ab, dann ist Zyklus mit Index i=k-1 im n.-Schritt zu Ende.
Ergebnis:
In n-Schritten haben wir n mal Indizesa[n], 0≤an≤9
ermittelt.
Zur Darstellung von d kann man jetzt alle Indizes in den n-Schritten von links
nach recht anordnen, zur Abgrenzung des ganzahligen Anteils a getrennt mit "Komma"
zu:
d = a,a1...an... , wobei die Pünktchen nach
an für den Fall stehen, daß der Zyklus nicht abbricht und n
unendlich wird. Ersetzen wir die an durch die im Zyklus ermittelten
Indizes (0...9), so erhalten wir die übliche Dez.Darstellung von Rat.-Zahlen.
Umgekehrt gilt auch: jede Zahl p/q kann durch einen elementaren Algorithmus (bereits in der Schule bekannt) in eine Dez.Zahlen-Darstellung umgewandelt werden:

z = 0* 100 +r1 10-1 . . . +rm 10-m
z = 0,r1r2 . . . rm
Satz1: Alle rationalen Zahlen r =p/q lassen sich als Potenzreihe der Form r =p *( (q+1)-1 +... +(q+1)-∞ ) darstellen.
Beweis: wegen Teilung des Eins-Elementes (z.B. b-Teilung, b natürl. Zahl), 1 *(b-1)= 1/b1 +1/b2 + . . . , siehe Abschnitt 1.13 zuvor, kann man durch setzen von b= (q+1)/p in Gleichung zuvor, diese umformen zu:
Folgerung zu Satz1: Die Partialsummen der Potenzreihe im Satz1 bilden eine konvergente Folge. Deshalb kann man feststellen: Alle rat.Zahlen sind Grenzwert einer konvergenten Folge, also Häufungspunkt in der Menge der Zahlen.
Bemerkung1: In der Folgerung2 im Abschnitt 1.13 zuvor hatten wir unendl. Potenreihen (aus Ganzen Z. =rat.Zahlen) angegeben, die sich nicht in rat.Zahlen p/q umwandeln lassen. Diese hießen "irrationale Zahlen", und als Beispiel hatten wir die Diagonale d eines 1-Quadrates genannt, d²=2.
Der Vollständigkeit halber sei hier eine Potenzreihen -Entwicklung für d angegeben:
davon: 0.7~ ln2= 1 -1/2 +1/3 + ... +(-1)(n+1) 1/n + . .
Algorithmus zur Ermittlung der wahren Länge eines Abstandes:
Sei d ein beliebiger Abstand und E das aktive Referenz-Eins-Element.
1.Schritt Im ersten Schritt ermitteln wir, wieviel mal d von E vollständig überdeckt wird (a'=a'*E). Dabei zerfällt a' in a +1, weil das letzte E i.a. darüber hinaus ragt (ansonsten ist Ermittlung zu Ende und a'=a ist ganze Zahl). Das letzte E bezeichnen wir als R (Rest). Beim nachfolg. Zyklus geht es genau um diesen Rest, der sukzessive entsteht, wenn wir E schrittweise teilen (Zoomfaktor f=10).
n.Schritt En = En-1/10 bilden und ermitteln, wieviel man R von En überdeckt wird (a'=a* En). Das besondere in diesen Teilungs-Schritten ist, dass a jetzt nicht mehr als ganze Zahl von 1-10 betrachtet wird, sondern als Index der 10-Teil-Abschnitte:
symb.:
Ergebnis:
In n-Schritten haben wir n mal Indizes
Bemerkung: Diesen konstruktiven, anschaulichen Ansatz zur Erklärung
von Rat.Zahlen werden wir in den Modellen zur analyt.Geometrie und
Analysis durch eine abstakte Herangehensweise (Fundamentalfolgen) ersetzen,
die nicht mehr die menschl. Vorstellungs-Kraft zur Erklärung benötigt.
Zusammenfassung
Zoomen: Beim "Zoomen" wird jedes (geometr.) Objekt hinsichtlich seiner
Ausdehnung (länge, Fläche, Winkel, Abstände usw.) formal mit einer Zahl >0 multipliziert,
wobei der Winkel als Div. 2-er Strecken gleich bleibt.
Ein neuer Aspekt beim Zoomen entseht durch das mehrfache Zoomen in eine Richtung, 0<f<1, dem Verkleinern. Offenbar wird die Ausdehnung eines Objektes bei unendl. mal Zoomen Null. Daraus resultiert folg. Frage: "Was passiert mt einem Objekt, dessen Ausdehnung im Grenzfall =Null ist ?"
Nach bisheriger Def. in Abschnitt 1.2 "Def. von Punkt und Gerade", hatten wir postuliert: Das einzige Objekt, das in allen Dim.j, 1≤j≤n die Ausdehnung Null hat, ist der Punkt.
Es gibt offenbar eine zweite Interpretation von Null: Durch das Zoomen, F={fn}, n->∞ können wir ebenso sagen: Auch im Grenzfall ist ein ein Dreieck noch ein Dreieck, ein Winkel noch ein Winkel, eine Fläche (z.B. Eins-Quadrat) noch eine Fläche, usw. ,trotz Ausdehnung=0.
Ergebnis: Bei dieser Betrachtungsweise (unendl.Zoomen) enstehen aus geometr. Objekten sogenannte "finite Elemente", deren Ausdehnung=Null ist, die aber theoretisch durch Multiplikation mit der Anzahl-Teilungen * n->∞ wieder-hergestellt werden können.
Messen und Vergleichen von Strecken: Wir haben die Zahlen bisher als Bemaßung von Strecken, Flächen usw. kennengelernt. Dabei ist wichtig zu wissen, das die Ausdehnung eines (geometr.) Objektes völlig neutral und wertfrei ist, und nur im Vergleich mit anderen Objekten hinsichtlich der Relation kleiner /gleich /größer eingeschätzt werden kann. So gesehen ist nicht die Länge einer Diagonalen d irrational, sondern das Verhältnis zu einer Referenz-Eins-Strecke.
Da die Eins-Strecke willkürlich zu einem Raum festgelegt/def. wird und sich von Fall zu Fall anders darstellt, ist der Zahlen-Typ von d von vonherein nicht festgelegt. Er kann alles sein: ganze Zahl -> irration.Zahl. Dabei gilt aber:
Beispiel Kreis: r=Radius, b=Kreisbogen-Länge, b/r =irrat.Zahl bei:
Fall-1: b=rat. ,r=irrat.
Fall-2: b=irrat. ,r=rat.
In der wirklichen Welt gibt es keine irrat.Zahlen, weil sie nur ein theor.Konstrukt (Grenzwert) aus existierenden Zahlen (rat.) sind.
Eine rat.Zahl kann man in endl.vielen Schritten aufschreiben, auf endl.viel Papier, und in einem begrenzten Zeitabschnitt wieder lesen (Erkennen). Das geht mit irrat.Zahlen nicht. Nach endl.vielen Schritten muß ich aufhören (z.B Auwertung Potenzreihe von Wurzel(2)), so daß Wurzel(2) real wieder zu einer rat.Zahl ist.
Folgerung: Alle Zahlen in der wirkl.Welt, lokaler-Raum, Newton-Raum sind existierende Rationale-Zahlen. Irrationale Zahlen können dagegen nur durch einem Namen auf sich verweisen (pi, e, usw.).
Für Berechnungen reichen Rat.Zahlen, wie im Computer realisiert durch Float mit 15 signifik.Stellen *10±99, völlig aus.
Die Genauigkeit im Erde-Mond-Bereich (400.000km) wäre dann 0,001mm , im Sonnen-System (Weltraum-Fahrt) 5Mrd.km dann 0,05m und bis α-Centauri (40Bio.km) dann ca. 100m.
->Anfang
Ein neuer Aspekt beim Zoomen entseht durch das mehrfache Zoomen in eine Richtung, 0<f<1, dem Verkleinern. Offenbar wird die Ausdehnung eines Objektes bei unendl. mal Zoomen Null. Daraus resultiert folg. Frage: "Was passiert mt einem Objekt, dessen Ausdehnung im Grenzfall =Null ist ?"
Nach bisheriger Def. in Abschnitt 1.2 "Def. von Punkt und Gerade", hatten wir postuliert: Das einzige Objekt, das in allen Dim.j, 1≤j≤n die Ausdehnung Null hat, ist der Punkt.
Es gibt offenbar eine zweite Interpretation von Null: Durch das Zoomen, F={fn}, n->∞ können wir ebenso sagen: Auch im Grenzfall ist ein ein Dreieck noch ein Dreieck, ein Winkel noch ein Winkel, eine Fläche (z.B. Eins-Quadrat) noch eine Fläche, usw. ,trotz Ausdehnung=0.
Ergebnis: Bei dieser Betrachtungsweise (unendl.Zoomen) enstehen aus geometr. Objekten sogenannte "finite Elemente", deren Ausdehnung=Null ist, die aber theoretisch durch Multiplikation mit der Anzahl-Teilungen * n->∞ wieder-hergestellt werden können.
Bemerkung: Die Arbeit mit diesen "finiten Elementen" füllt
einen ganzen Zweig der Mathematik aus, der sog. "Infinitesimal-Rechnung".
In den nachf. Abhandlungen zur analyt.Geometrie und Analysis
gehen wir darauf näher ein.
Messen und Vergleichen von Strecken: Wir haben die Zahlen bisher als Bemaßung von Strecken, Flächen usw. kennengelernt. Dabei ist wichtig zu wissen, das die Ausdehnung eines (geometr.) Objektes völlig neutral und wertfrei ist, und nur im Vergleich mit anderen Objekten hinsichtlich der Relation kleiner /gleich /größer eingeschätzt werden kann. So gesehen ist nicht die Länge einer Diagonalen d irrational, sondern das Verhältnis zu einer Referenz-Eins-Strecke.
Da die Eins-Strecke willkürlich zu einem Raum festgelegt/def. wird und sich von Fall zu Fall anders darstellt, ist der Zahlen-Typ von d von vonherein nicht festgelegt. Er kann alles sein: ganze Zahl -> irration.Zahl. Dabei gilt aber:
Beispiel Kreis: r=Radius, b=Kreisbogen-Länge, b/r =irrat.Zahl bei:
Fall-1: b=rat. ,r=irrat.
Fall-2: b=irrat. ,r=rat.
In der wirklichen Welt gibt es keine irrat.Zahlen, weil sie nur ein theor.Konstrukt (Grenzwert) aus existierenden Zahlen (rat.) sind.
Eine rat.Zahl kann man in endl.vielen Schritten aufschreiben, auf endl.viel Papier, und in einem begrenzten Zeitabschnitt wieder lesen (Erkennen). Das geht mit irrat.Zahlen nicht. Nach endl.vielen Schritten muß ich aufhören (z.B Auwertung Potenzreihe von Wurzel(2)), so daß Wurzel(2) real wieder zu einer rat.Zahl ist.
Folgerung: Alle Zahlen in der wirkl.Welt, lokaler-Raum, Newton-Raum sind existierende Rationale-Zahlen. Irrationale Zahlen können dagegen nur durch einem Namen auf sich verweisen (pi, e, usw.).
Für Berechnungen reichen Rat.Zahlen, wie im Computer realisiert durch Float mit 15 signifik.Stellen *10±99, völlig aus.
Die Genauigkeit im Erde-Mond-Bereich (400.000km) wäre dann 0,001mm , im Sonnen-System (Weltraum-Fahrt) 5Mrd.km dann 0,05m und bis α-Centauri (40Bio.km) dann ca. 100m.
Bemerkung: Eine genauere Untersuchung von rationalen und
reellen Zahlen erfolgt in der Abhandlung:
3. Modell der rellen Zahlen
Weitere Betrachtungen:
Euklidische Geometrie ,
Modell der reellen Zahlen ,
analytische Geometrie I ,
analytische Geometrie II ,
Euklidischer Raum ,
Analysis 1, Abbildungen ,
kleinere Beispiele der Himmelsmechanik im Newton-Modell ,
Bewegungen im Newton-Raum ,