Temp_64.jpg return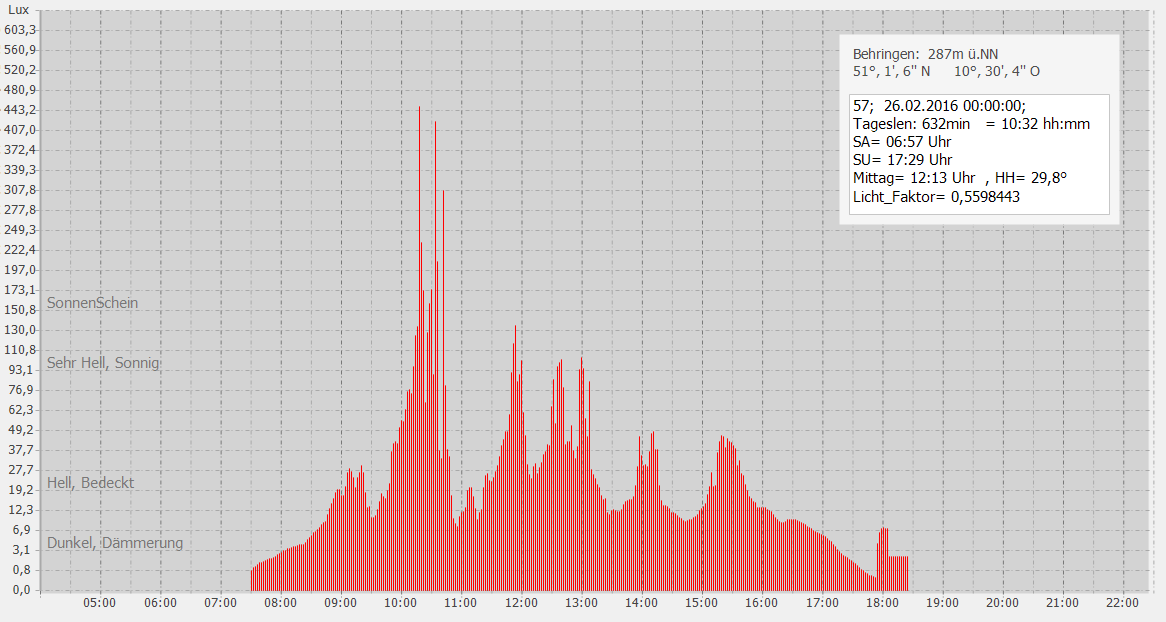 Theoretische Grundlagen: Bei einem homogenen Lichtstrom von einer zentralen Quelle aus kommen an allen Orten im Abstand r=const. von Quelle die gleiche Menge (Intensitaet) an Licht-Photonen an. Diese Orte bilden eine sog. Kugel-Sphaere (S), mit Radius r und Oberflaeche(S(r))= 4*math.pi* r*r um LichtQuelle. Das Verhaeltnis der Oberflaechen 2-er Sphaeren, S(r1) u.S(r2), berechnet sich dann wie folgt: r2=r *r1 -> S(r1) / S(r2) = (r1*r1) / (r1*r1) * r*r = 1/r*r Wenn man beruecksichtigt, dass sich die Luxe aus Lichtstrom/Flaeche berechnen, dann wuerden sich bei 1>r die Luxe um r-Quadrat vergroessern und bei r>1 entspr. verkleinern! Betrachten wir die Punkte des euklid.Raumes als Richtungen (0->P), P∈R³ dann erhalten wir ein Zentral-Vektorfeld durch Zuordnung der Punkte zu Richtungen(Vektoren) wie folgt: ℜ(r) ,r=Vektor: r=(0->P)=-(P->0) ,P=(x,y,z) Zur besseren Handhabung nehmen wir noch die Normierung: r₀=r/Betrag(r) vor, d.h. in dieser Notation bezeichnen wir im Folgeden mit r₀ den Einsvektor zu Vektor(r) und mit r den Betrag(Vektor(r)). Die formale Schreibweise fuer das zentrale VektorFeld lautet dann: (1) ℜ = f(r₀)*{r*r₀} , r²=x²+y²+z² , f= reelle Funktion. d.h. jedem Punkt wird eine reelle Zahl zugeordnet. Um die Verbindung zum vorliegenden LichtStrom-Feld herzustellen, denken wir uns die Punkte(Vektoren) in Kugel- Koord.: r₀ =(x,y,z) = r*(cos(α)*sin(β), sin(α)*sin(β), cos(β)) , α=Winkel in x,y-Ebene , und setzen f(r₀) fest zu: (2) f(r₀) = C/r³ , (2) in (1) einsetzen, dann erhaelt man: ℜ = (C/r³) * r* {r₀(r,α,β} = C/r² * {r₀(r,α,β)} Offensichtlich sind jetzt die Faktoren C/r² nicht mehr von den Winkeln α,β abhaengig und fuer die Sphaeren S(r) constant=C (das spez.SphaerenVerhaeltnis S(r1)/S(r2) wird hier zu S(r)/S(1) verallgemeinert). Im Feld ℜ = C/r² * {r₀(r,α,β} sind jetzt die Punkte P, P∈S(1), mit Wert =C belegt! und alle weiteren S(r) mit C/r² Folgerung: Betrachtet man die Kugel K(r) im Feld ℜ als Integrations-Gebiet, so kann mit der Eins-Funtion f=1 ueber die Kugel integriert werden und man erhaelt eine reelle Zahl fuer das Integrations-Gebiet(hier Kugel), die als Volumen dieses Gebietes gilt(hier Kugel-Inhalt): ∫k(r) [1⋅dv] dv =VolumenElement =dx⋅dy⋅dz = r²⋅sin(β)⋅dr⋅dα⋅dβ Integr.Grenzen fuer α = [-π -> +π] Integr.Grenzen fuer β = [ 0 -> +π ] -> ∫r²dr=r³/3 , ∫sin(β)dβ=-cos(β)=-(-1 -1)=2 , ∫dα=α=(π-(-π))=2π Dies ergibt V(Kugel(r))= (r³/3 ) * 2 * 2π = 4/3⋅π⋅r³ Wenn die Integration ueber r festgehalten wird, also Sphaere S(r), dann folgt fuer das Volumen der Sphaere: ∫(S(r)) *1 *dS = ∫(S(r=fest,α,β)) *[r²⋅sin(β)⋅dr⋅dα⋅dβ] = r² * 2 * 2π = 4⋅π⋅r² Wenden wir dieses Ergebnis auf unsere Feldgleichung (2) an, so erhalten wir eine Beziehung fuer die Wirkung des Feldes an allen Punkten mit Abstand r von Quelle wie folgt: ℜ(r=fest) = C⋅4⋅math.pi * {r₀} also konstant, wie vorausgesetzt! return |
2-Licht-Quellen: (26.2.2016)
Das Interessante an diesem Tag sind die beiden rosa Rechtecken ab 18:00 Uhr. |
|---|